五子棋AI教程第二版三:极小化极大值搜索
lihongxun945 opened this issue · 16 comments
AI实现的基本思路-极大极小值搜索算法
从这一章开始我们讲算法,我会贴出关键的代码,因为完整的代码太长,所以强烈建议大家先 clone 下这个仓库,当讲到代码的时候也去对应的文件看看完整代码: https://github.com/lihongxun945/gobang
五子棋看起来有各种各样的走法,而实际上把每一步的走法展开,就是一颗巨大的博弈树。在这个树中,从根节点为0开始,奇数层表示电脑可能的走法,偶数层表示玩家可能的走法。
假设电脑先手,那么第一层就是电脑的所有可能的走法,第二层就是玩家的所有可能走法,以此类推。
我们假设平均每一步有50种可能的走法,那么从根节点开始,往下面每一层的节点数量是上一层的 50被,假设我们进行4层思考,也就是电脑和玩家各走两步,那么这颗博弈树的最后一层的节点数为 50^4 = 625W 个。
先不考虑这么多个节点需要多久能算出来。有了对博弈树的基本认识,我们就可以用递归来遍历这一棵树。
那么我们如何才能知道哪一个分支的走法是最优的,我们就需要一个评估函数能对当前整个局势作出评估,返回一个分数。我们规定对电脑越有利,分数越大,对玩家越有利,分数越小,分数的起点是0。
我们遍历这颗博弈树的时候就很明显知道该如何选择分支了:
- 电脑走棋的层我们称为 MAX层,这一层电脑要保证自己利益最大化,那么就需要选分最高的节点。
- 玩家走棋的层我们称为MIN层,这一层玩家要保证自己的利益最大化,那么就会选分最低的节点。
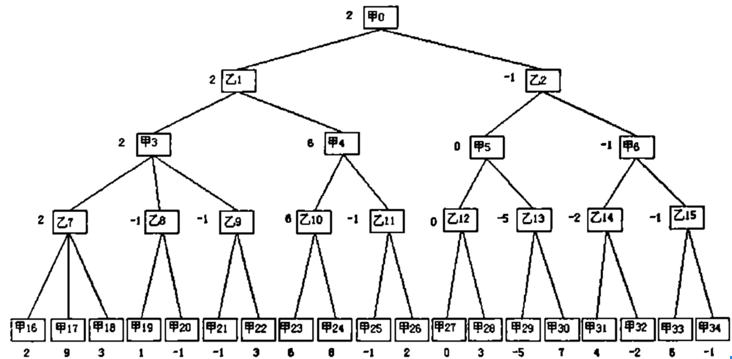
这也就是极大极小值搜索算法的名称由来。这是维基百科上的一张图:
此图中甲是电脑,乙是玩家,那么在甲层的时候,总是选其中值最大的节点,乙层的时候,总是选其中最小的节点。
而每一个节点的分数,都是由子节点决定的,因此我们对博弈树只能进行深度优先搜索而无法进行广度优先搜索。深度优先搜索用递归非常容易实现,然后主要工作其实是完成一个评估函数,这个函数需要对当前局势给出一个比较准确的评分。
极大极小值搜索
五子棋是一个1515的棋盘,因为棋盘大小不会变动,所以目前来看用 1515 的二维数组来存储,效果是最好的。极小化极大值搜索,正常需要两个函数,一个搜索极小值,一个搜索极大值。因为其实大部分逻辑是一样的,完全可以把这两个函数合并成一个。然后把对手的分数变成负的,就是我方的分数。这种实现就是负极大值搜索。代码如下:
negamax.js
var r = function(deep, alpha, beta, role, step, steps, spread) {
var _e = board.evaluate(role)
var leaf = {
score: _e,
step: step,
steps: steps
}
return leaf
}
var best = {
score: MIN,
step: step,
steps: steps
}
// 双方个下两个子之后,开启star spread 模式
var points = board.gen(role)
if (!points.length) return leaf
for(var i=0;i<points.length;i++) {
var p = points[i]
board.put(p, role)
var _deep = deep-1
var _spread = spread
var _steps = steps.slice(0)
_steps.push(p)
var v = r(_deep, -beta, -alpha, R.reverse(role), step+1, _steps, _spread)
v.score *= -1
board.remove(p)
// 省略剪枝代码
}
return best
}删除了很多跟本章节无关的代码,其实代码非常简单,就是一个递归实现的深度优先搜索。如果你觉得读起来有困难,可以先复习一下数据结构和算法。这里唯一需要注意的就是,v.score *= -1 这一行代码,这是负极大值实现的关键代码。
评估函数
上面的代码是无法运行的,因为有了搜索策略,我们还需要进行局势的评估。我们简单的用一个整数表示当前局势,分数越大,则自己优势越大,分数越小,则对方优势越大,分数为0是表示双方局势相当。
在源码中 board.js 中的 evaluate 就是评估函数,它接受一个角色,因为分数是相对角色而言的,返回一个整型数。比如如果对电脑是1000分,那么同样的局势对人类棋手就会返回 -1000 分。
我们对五子棋的评分是简单的把棋盘上的各种连子的分值加起来得到的,对各种连子的基本评分规则如下:
- 连五,100000
- 活四, 10000
- 活三 1000
- 活二 100
- 活一 10
如果一侧被封死但是另一侧没有,则评分降一个档次,也就是死四和活三是相同的分
- 死四, 1000
- 死三 100
- 死二 10
score.js 中是对各种情况估值的定义。
按照这个规则把棋盘上电脑的所有棋子打分,之和即为电脑的单方面得分 scoreComputer,然后对玩家的棋子同样打分 得到 scoreHuman。
scoreComputer - scoreHuman 即为当前局势的总分数。
那么如何找出所有的连子呢,目前我的方式是遍历数组,一个个的数。因为代码量比较大,在这里我不会贴出代码,请自行参阅源码中的 evaluate-point.js 文件,他就是对单个点进行评分的模块。
请注意,这里我们说的评估函数是对整个棋局的评估,后面讲启发式搜索的时候还会有一个启发式评估函数是对某一个位置的评估。这两个评估是不同的。
着法生成
generator顾名思义,就是在每一步生成所有可以落子的点。并不是所有的空位我们又要搜索,很多位置明显不合适的我们可以直接排除。
这个函数非常重要,可以看到源码中这个函数非常长,因为我们要尽可能删除无用点,尽可能做更好的排序,这样才能最大限度发挥Alpha-beta 剪枝的效果。
因为代码量较大,这里只贴出部分代码:
board.js
gen (role, onlyThrees, starSpread) {
//省略...
// 遍历棋盘
for(var i=0;i<board.length;i++) {
for(var j=0;j<board.length;j++) {
var p = [i, j]
if(board[i][j] == R.empty) {
var scoreHum = p.scoreHum = this.humScore[i][j]
var scoreCom = p.scoreCom = this.comScore[i][j]
var maxScore = Math.max(scoreCom, scoreHum)
p.score = maxScore
p.role = role
//省略部分代码,根据p的分数,把它放到对应的结果中
}
}
}
// 省略排序代码
return result
}另外一些简单的函数,没有列出,直接去看源码就行了。
下面我们将讲一个重点: Alpha Beta 剪枝算法。
return leaf 这前面if被删了
为什么代码库是404
@Dzzzy 多打了一个标点,现在好了
@Dzzzy 多打了一个标点,现在好了
谢谢!我给您发了一封邮件希望您能回复!
It would be nice if there were some comments in the code.
请问……star spread是什么啊,没搜到orz
请问极大极小搜索树的根节点是什么 如果考虑所有的可行落子点 那么 每一步都下一个节点都会有15*15-当前落子点个数 就算有剪枝函数 应该也会很慢吧
为什么评估整体棋盘的函数写的那么简略,感觉这一部分也有很多值得优化的问题啊,而且我没找到评估整体棋盘的函数
@jinchiniao 作者设计的评估函数是棋盘上所有空位的得分加起来,在board.js的evaluate(role)里面。
请问……star spread是什么啊,没搜到orz
自己写的一段逻辑,查不到是正常的。
请问极大极小搜索树的根节点是什么 如果考虑所有的可行落子点 那么 每一步都下一个节点都会有15*15-当前落子点个数 就算有剪枝函数 应该也会很慢吧
看下一篇剪枝算法,能解答你的疑惑
@lihongxun945 您好:
我在vcx.js的min函式裡看到board.win()這個函式被呼叫,但是我卻找不到win的程式碼。而win.js這個模組似乎也沒有被其他檔案import,請問這是為甚麼?
如果搜索的是6层,那第六层的的评估局面也是棋盘上所有空位的得分,那计算量应该是到^7了吧?还是说评估局面的函数不是这么算的?
negamax函数里,在put以后没有对棋盘的value进行更新,所以进一步搜索的时候每次对当前局面进行evaluate的时候都是使用了以前没有更新过的value,这正确性是不是不太对
只进攻,没有防守吗
代码错误都不带修复的吗