This repo contains my online evolving book Essentials of Mathematical Methods: Foundations, Principles, and Algorithms. This book surveys fundamental results in major branches of applied mathematics, with emphasized applications in stochastic system modeling, statistical learning, and optimal decision-making.
This book will be free of charge. You can support me by purchasing it from LeanPub. If you have any questions or suggestions, you can create a pull request or send me an email at yangyutu123@gmail.com
Linear Algebra and Matrix Analysis
Mathematical Optimization
Probability and Statistical Estimation
Stochastic Process
Markov Chain and Random Walk
Linear Regression Analysis
Statistical Learning
Neural Network and Deep Learning
(Deep) Reinforcement Learning
- Sets, Sequences and Series
- Metric Space
- Advanced Calculus
- Linear Algebra and Matrix Analysis
- Basic Functional Analysis
- Unconstrained Nonlinear Optimization
- Constrained Nonlinear Optimization
- Linear Optimization
- Convex Analysis and Convex Optimization
- Basic Game Theory
- Probability Theory
- Statistical Distributions
- Statistical Estimation Theory
- Multivariate Statistical Methods
- Linear Regression Analysis
- Monte Carlo Methods
- Models and estimation in linear systems
- Stochastic Process
- Stochastic Calculus
- Markov Chain and Random Walk
- Time Series Analysis
- Supervised Learning Principles and Methods
- Linear Models for Regression
- Linear Models for Classification
- Generative Models
- K Nearest Neighbors
- Tree Methods
- Ensemble and Boosting Methods
- Unsupervised Statistical Learning
- Neural Network and Deep Learning
You are free to redistribute the material in any medium or format under the following terms:
-Attribution: You must give appropriate credit, provide a link to the license, and indicate if changes were made. You may do so in any reasonable manner, but not in any way that suggests the licensor endorses you or your use.
-NonCommercial: You may not use the material for commercial purposes.
*The licensor cannot revoke these freedoms as long as you follow the license terms. This licence is created via creative commons (https://creativecommons.org). If you have any questions regarding the license, please contact the author.
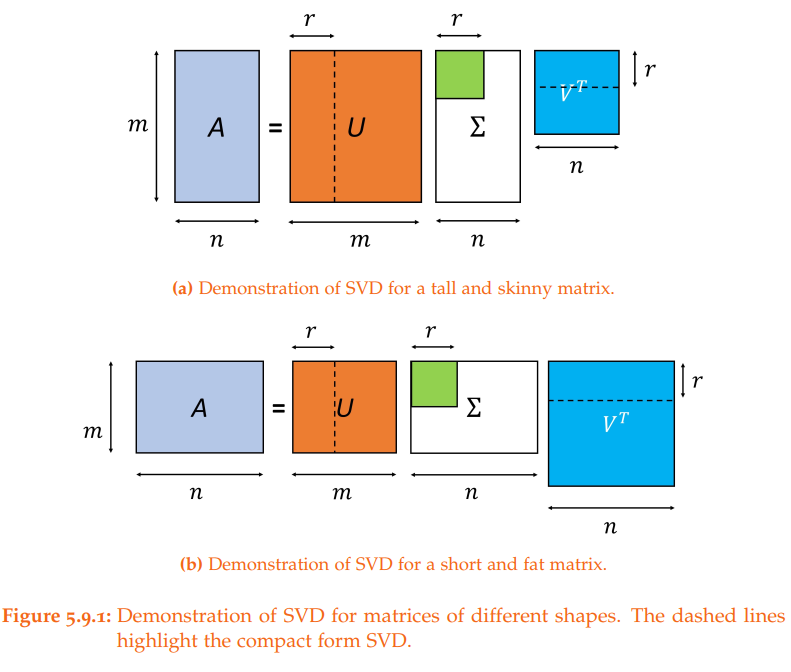
SVD (Singular Value Decomposition) is one of the most important results in linear algebra. It is the cornerstone of many important methods in applied math, statistics, and machine learning. This books summarizes the properties of SVD with the following theorem and diagram. The proof is concise with all the supporting theorems and lemma included in the book.
The following diagram shows the shape of resulting matrices and captures the relationship between complete SVD and compact SVD.
A common mistake on the relationship between U and V is discussed as wells.
In multivariate Gaussian statistics, the affine transformation theorem is used to prove a number of important properties of Gaussian random variables (such as addition, condition, etc.). This book first gives a proof of this theorem based on moment generating functions.
Then the book gives the application of this theorem to the sum of multivariate Gaussian random variables. It is worth mentioning that the author emphasizes in the footnote that these result only hold when the joint normality conditions holds.
SVM, logistic regression and Perceptron learning are commonly used linear classification model in machine learning. The three models can be unified under the same mathematical optimization framework, with each method corresponds to a different loss function. This book elaborates and shows how to transform these three models into this unified framework.
Value iteration is one of the cornerstone theorems in reinforcement learning. However, many textbooks and online resources simply skip the proof. This book puts together a concise proof through contraction mapping and fixed point theorem. The contraction mapping and fixed point theorem, which are important tools in applied math, are introduced in detail in Part I of this book.
Then the book gives an algorithm based on the value iteration theorem.