Comparison of mean cumulative count curves via the area under the curve (AUC)

Zachary R. McCaw
Updated: 2022-05-19

Description

This package provides functions for inference on the difference and ratio in AUCs comparing two mean cumulative count (MCC) curves. The MCC curves are estimated using an approach based on the method of Ghosh and Lin (2000), which accounts for the presence of terminal competing risks. Also see:

CICs for comparing cumulative incidence curves.

Installation

devtools::install_github(repo = 'zrmacc/MCC')

Methods

Estimation of the mean cumulative count curve

For each study arm, the MCC is estimated as follows. Define $N(\cdot)$ as the counting process for events of interest, both terminal and non-terminal, $Y(\cdot)$ as the number of subjects who remain at risk, and $S(\cdot)$ as the probability of not having experienced a terminal event. The MCC $\mu(t)$ at time $t$ is estimated by: $$ \mu(t) = \int_{0}^{t} \hat{S}(u) \frac{ dN(u) }{ Y(u) } $$

Here $\hat{S}(u)$ is the Kaplan-Meier estimate of the probability of being terminal event-free, estimated from all terminal events, both those of interest and those regarded as a competing risk; $dN(u)$ is the number of events of interest, both non-terminal and terminal, occurring at time $u$; and $Y(u)$ is the number of subjects who remain at risk, which are subjects who have neither been censored nor experienced a terminal event.

Data

The function GenData simulates example data in the format expected by this package. The recurrent event times are generated from a Poisson process that continues until censoring or death, whichever occurs first. Optionally, a gamma frailty_variance may be specified such that the patient-specific event and death rates are correlated. The example data includes 100 patients in each of the treatment and control arms. The maximum duration of follow-up is tau = 4 (e.g. years). The rate of recurrent events for patients in the treatment arm is 80% the rate for patients in the control arm.

library(MCC)
covariates <- data.frame(
  arm = c(rep(1, 100), rep(0, 100))
)
data <- MCC::GenData(
  beta_event = c(log(0.8)),
  covariates = covariates,
  frailty_variance = 0.2,
  tau = 4
)
head(data)

##   idx status       time arm cens_rate death_rate event_rate   frailty
## 1   1      1 0.08845737   1      0.25  0.1888051  0.6041762 0.7552202
## 2   1      2 0.23565323   1      0.25  0.1888051  0.6041762 0.7552202
## 3   2      1 0.16410134   1      0.25  0.1884027  0.6028886 0.7536108
## 4   2      1 0.66910083   1      0.25  0.1884027  0.6028886 0.7536108
## 5   2      2 0.87297407   1      0.25  0.1884027  0.6028886 0.7536108
## 6   3      2 0.02295830   1      0.25  0.3140817  1.0050614 1.2563267

The essential data are:

idx, the subject index.
time, the observation time.
status, coded 0 for censoring, 1 for an event, 2 for death (or any competing terminal event).
arm, coded as 1 for treatment, 0 for reference.

For analyzing other data sets, arm and status should have the same coding. Each subject should experience an observation-terminating event, i.e. either death or censoring.

The example data also include:

true_death_rate, the patient-specific terminal event rate, calculated as frailty x base_death_rate x exp(covariates %*% beta_death). If omitted, beta_death is set to zero.
true_event_rate, the patient-specific recurrent event rate, calculated as frailty x base_event_rate x exp(covariates %*% beta_event). If omitted, beta_event is set to zero.
frailty,the patient-specific frailty drawn from a gamma distribution with mean 1 and the specified variance.

Observation-terminating events

In contrast to the time to first event setting, in the multiple or recurrent events setting, a subject may remain at risk after experiencing an event of interest. An observation-terminating event, either censoring or the occurrence of a competing risk, is therefore necessary to remove a subject from the risk set. Conversely, a subject who lacks an observation-terminating event is implicitly assumed to remain at risk indefinitely. If a subject lacks an observation-terminating event, then by default CompareAUCs will add a censoring time immediately after their last event of interest. For example, if the data for subject 1 were:

##   idx time status
## 1   1    2      1
## 2   1    3      1
## 3   1    5      1

then, for analysis, the subject is assumed to have been censored after the last event, as in the following:

##   idx time status
## 1   1    2      1
## 2   1    3      1
## 3   1    5      1
## 4   1    5      0

If a subject who lacks an observation-terminating event should, in fact, remain at risk indefinitely, set cens_after_last = FALSE.

Terminal events of interest

Suppose the endpoint of interest includes a fatal event. One such endpoint is heart failure hospitalization (HFH) or cardiovascular (CV)-death. In this setting, it becomes necessary to distinguish non-fatal events of interest (e.g. HFH), after which the subject remains in the risk set, from fatal events of interest (e.g. CV-death), after which the subject is removed from the risk set. To achieve this, a fatal event of interest should be recorded using two records. The first, with status = 1, indicates that an event of interest has occurred. The second, with status = 2, indicates that the event was terminal. For example, the following data indicate that subject 1 had 3 events of interest, and that the 3rd event, occurring at time = 5, was terminal.

##   idx time status
## 1   1    2      1
## 2   1    3      1
## 3   1    5      1
## 4   1    5      2

By contrast, the following data indicate that subject 2 had 3 events of interest, none of which was terminal:

##   idx time status
## 1   2    2      1
## 2   2    3      1
## 3   2    5      1

Note that, by default, subject 2 is assumed to have been censored after their 3rd event of interest, as in the following:

##   idx time status
## 1   2    2      1
## 2   2    3      1
## 3   2    5      1
## 4   2    5      0

Although censoring (status = 0) and a terminal event (status = 2) both remove a subject from the risk set, there is an important distinction. Censoring leaves open the possibility that the subject experienced more events of interest in the future, whereas a terminal event precludes the possibility of any future events of interest.

Analyses

AUCs

To compare the areas under the mean cumulative count curves up to time $\tau = 4$:

aucs <- MCC::CompareAUCs(
  data,
  tau = 4,
  boot = TRUE,
  perm = TRUE,
  reps = 200,
  alpha = 0.05
)
show(aucs)

## Marginal Areas:
##   arm   n area    se tau
## 1   0 100 6.29 0.568   4
## 2   1 100 4.31 0.476   4
## 
## 
## CIs:
##       method contrast observed     se  lower  upper
## 1 asymptotic    A1-A0   -1.980 0.7410 -3.430 -0.530
## 3  bootstrap    A1-A0   -1.980 0.7480 -3.400 -0.616
## 2 asymptotic    A1/A0    0.685 0.0978  0.518  0.906
## 4  bootstrap    A1/A0    0.685 0.0994  0.508  0.890
## 
## 
## P-values:
##        method contrast observed       p
## 1  asymptotic    A1-A0   -1.980 0.00748
## 3   bootstrap    A1-A0   -1.980 0.00995
## 5 permutation    A1-A0   -1.980 0.00995
## 2  asymptotic    A1/A0    0.685 0.00801
## 4   bootstrap    A1/A0    0.685 0.00995
## 6 permutation    A1/A0    0.685 0.00995

Here:

tau is the truncation time, or the time up to which the AUC is calculated.
boot indicates to construct bootstrap confidence intervals.
perm indicates to perform permutation tests for the difference and ratio of AUCs.
reps is the number of simulation replicates.
- The bootstrap is grouped by idx, and stratified by strata, if applicable.
alpha is 1 minus the desired coverage for confidence intervals.

Stratified Analysis

CompareAUCs also allows for stratified analysis. Consider a data set, similar to that described previously, but with the additional of a binary stratification factor. The event rate for individuals in stratum 1 is increased by 20%.

# Generate data with strata.
covariates <- data.frame(
  arm = c(rep(1, 100), rep(0, 100)),
  strata = stats::rbinom(200, 1, 0.25)
)
data <- MCC::GenData(
  beta_event = c(log(0.8), log(1.2)),
  covariates = covariates,
  frailty_variance = 0.2,
  tau = 4
)

# Stratified AUC analysis.
aucs <- MCC::CompareAUCs(
  data,
  strata = data$strata,
  tau = 4,
  boot = TRUE,
  perm = TRUE,
  reps = 200,
  alpha = 0.05
)
show(aucs)

## Marginal Areas:
##   arm   n area    se tau
## 1   0 100 5.85 0.608   4
## 2   1 100 5.51 0.597   4
## 
## 
## CIs:
##       method contrast observed    se  lower upper
## 1 asymptotic    A1-A0   -0.338 0.852 -2.010  1.33
## 3  bootstrap    A1-A0   -0.338 0.867 -1.860  1.21
## 2 asymptotic    A1/A0    0.942 0.141  0.702  1.26
## 4  bootstrap    A1/A0    0.942 0.146  0.720  1.24
## 
## 
## P-values:
##        method contrast observed     p
## 1  asymptotic    A1-A0   -0.338 0.692
## 3   bootstrap    A1-A0   -0.338 0.697
## 5 permutation    A1-A0   -0.338 0.846
## 2  asymptotic    A1/A0    0.942 0.692
## 4   bootstrap    A1/A0    0.942 0.697
## 6 permutation    A1/A0    0.942 0.846

Outputs

The output of CompareAUCs is an object with these slots.

@StratumAreas containing the stratum-specific AUCs for each arm.

aucs@StratumAreas

##   arm strata  n tau     area var_area   se_area weight
## 1   0      0 76   4 5.045419 34.65885 0.6753055   0.74
## 2   0      1 24   4 8.145358 42.53490 1.3312729   0.26
## 3   1      0 72   4 5.029110 31.44486 0.6608587   0.74
## 4   1      1 28   4 6.892973 48.72342 1.3191369   0.26

@MargAreas containing the AUCs for each arm, marginalized over any strata.

aucs@MargAreas

##   arm   n     area        se tau
## 1   0 100 5.851403 0.6078921   4
## 2   1 100 5.513715 0.5973172   4

@CIs containing confindence intervals for the difference and ratio of AUCs.

aucs@CIs

##       method contrast   observed        se      lower    upper
## 1 asymptotic    A1-A0 -0.3376884 0.8522445 -2.0080569 1.332680
## 3  bootstrap    A1-A0 -0.3376884 0.8672591 -1.8618497 1.214607
## 2 asymptotic    A1/A0  0.9422893 0.1414339  0.7021378 1.264580
## 4  bootstrap    A1/A0  0.9422893 0.1456046  0.7199988 1.236457

@MCF containing the per arm mean cumulative count curve, averaged across strata.

head(aucs@MCF)

##          time         mcf     var_mcf     se_mcf arm
## 1 0.004363264 0.009285714 0.002328061 0.04824999   1
## 2 0.016617209 0.019563492 0.009827984 0.09913619   1
## 3 0.023142688 0.028849206 0.011983596 0.10946961   1
## 4 0.024007674 0.039126984 0.019272254 0.13882454   1
## 5 0.037141490 0.048412698 0.021255417 0.14579238   1
## 6 0.039660038 0.057698413 0.023066131 0.15187538   1

@Pvals containing the bootstrap and permutation p-values.

aucs@Pvals

##        method contrast   observed         p
## 1  asymptotic    A1-A0 -0.3376884 0.6919322
## 3   bootstrap    A1-A0 -0.3376884 0.6965174
## 5 permutation    A1-A0 -0.3376884 0.8457711
## 2  asymptotic    A1/A0  0.9422893 0.6920809
## 4   bootstrap    A1/A0  0.9422893 0.6965174
## 6 permutation    A1/A0  0.9422893 0.8457711

@Reps is a list containing the bootstrap and permutation test statistics.

Adjusted AUCs

The previous estimator allows for stratification, but a different approach is needed to accommodate continuous covariates. If covariates are provided, then CompareAUCs uses an augmentation estimator to adjust for differences between the treatment groups. Note that strata and covariates should not both be provided. If adjustment for both is needed, use model.matrix to generate a design matrix including both covariates and stratum indicators, e.g. model.matrix(~ 0 + covar + strata, data = data), then supply the design matrix covar argument.

# Generate data with a continuous covariate.
covariates <- data.frame(
  arm = c(rep(1, 100), rep(0, 100)),
  covar = stats::rnorm(200)
)
data <- MCC::GenData(
  beta_event = c(log(0.8), log(1.2)),
  covariates = covariates,
  frailty_variance = 0.2,
  tau = 4
)

aucs <- MCC::CompareAUCs(
  data,
  tau = 4,
  boot = TRUE,
  perm = TRUE,
  reps = 200,
  alpha = 0.05
)
show(aucs)

## Marginal Areas:
##   arm   n area    se tau
## 1   0 100 5.74 0.579   4
## 2   1 100 5.28 0.612   4
## 
## 
## CIs:
##       method contrast observed    se lower upper
## 1 asymptotic    A1-A0   -0.467 0.843 -2.12  1.18
## 3  bootstrap    A1-A0   -0.467 0.877 -2.11  1.35
## 2 asymptotic    A1/A0    0.919 0.141  0.68  1.24
## 4  bootstrap    A1/A0    0.919 0.147  0.68  1.25
## 
## 
## P-values:
##        method contrast observed     p
## 1  asymptotic    A1-A0   -0.467 0.579
## 3   bootstrap    A1-A0   -0.467 0.607
## 5 permutation    A1-A0   -0.467 0.577
## 2  asymptotic    A1/A0    0.919 0.581
## 4   bootstrap    A1/A0    0.919 0.607
## 6 permutation    A1/A0    0.919 0.577

Plotting

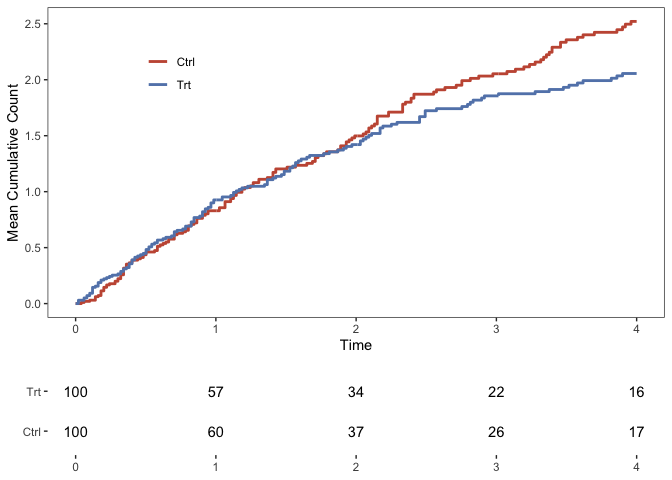
The function PlotMCFs plots the mean cumulative count curves, comparing two treatment arms. Note that data must contain the column arm.

q <- MCC::PlotMCFs(data)
q_nar <- MCC::PlotNARs(
  data = data,
  x_breaks = seq(from = 0, to = 4)
)
q_main <- cowplot::plot_grid(
  plotlist = list(q, q_nar),
  nrow = 2,
  align = "v",
  axis = "l",
  rel_heights = c(3, 1)
)
show(q_main)

liuminzhao/MCC