水平集图像分割
1. 水平集变分推导
能量函数: $$ \varepsilon_{g,\lambda,\nu} = \lambda\mathcal{L}(\phi)+\nu\mathcal{A}g(\phi) $$ 其中: $$ \mathcal{L}g=\int{\Omega}g\delta(\phi)|\nabla\phi|dxdy,\qquad \mathcal{A}g=\int{\Omega}gH(-\phi)dxdy,\qquad g=\frac{1}{1+|\nabla G{\sigma}I|} $$ 水平集的优化目标是求得使其能量函数$\varepsilon_{g, \lambda, \nu}$能量最小的曲面$\phi$,即 $$ \phi^=\arg \min(\varepsilon_{g,\lambda,\nu})=\arg \min (\lambda\mathcal{L}(\phi)+\nu\mathcal{A}_g(\phi)) $$ 使用变分法对其进行求解:
首先来看第一项: $$ \mathcal{L}g=\int{\Omega}g\delta(\phi)|\nabla\phi|dxdy $$ 令$F(\phi)=g\delta(\phi)|\nabla\phi|$, 取一个很小的$\varepsilon$和一个随机函数$h$,满足$h|_{\partial \Omega}=0$,则 $$ \begin{aligned} F(\phi+\varepsilon h)&=g\delta(\phi+\varepsilon h)|\nabla(\phi+\varepsilon h)| \ &=g\delta(\phi+\varepsilon h)\sqrt{(\phi + \varepsilon h)_x^2+(\phi+\varepsilon h)_y^2} \end{aligned} $$ 对偏移量$\varepsilon$进行求导: $$ \frac{\partial F(\phi+\epsilon h)}{\partial \varepsilon}=gh\delta '(\phi+\varepsilon h)|\nabla(\phi+\varepsilon h)| + g\delta (\phi+\varepsilon h)\frac{h_x(\phi+\varepsilon h)_x + h_y(\phi+\varepsilon h)_y}{\sqrt{(\phi+\varepsilon h)_x^2+(\phi+\varepsilon h)_y^2}} $$
所以
$$
\frac{\partial \mathcal{L_g}(\phi+\varepsilon h)}{\partial \varepsilon}\bigg |{\varepsilon\rightarrow0}=\int{\Omega}gh\delta'(\phi)|\nabla\phi|dxdy+\int_{\Omega}g\delta(\phi)\frac{h_x\phi_x+h_y\phi_y}{\phi^2_x+\phi^2_y}dxdy
$$
其中,$\delta(\phi)=1if\phi=0else0$,因此式(7)中的第一项为零,式(7)可以进行进一步简化
$$
\begin{aligned}
\frac{\partial \mathcal{L_g}(\phi+\varepsilon h)}{\partial \varepsilon}\bigg |{\varepsilon\rightarrow0}
&=\int{\Omega}g\delta(\phi)\frac{h_x\phi_x+h_y\phi_y}{\phi^2_x+\phi^2_y}dxdy\
&=\int_{\Omega}\left[ \frac{\partial}{\partial x}(\frac{\phi_xg\delta(\phi)h}{|\nabla \phi|})+\frac{\partial}{\partial y}(\frac{\phi_y g\delta(\phi)h}{|\nabla \phi|})\right]dxdy
-\int_{\Omega} \left[ \frac{\partial}{\partial x}(\frac{\phi_x g \delta(\phi)}{|\nabla \phi|})h+\frac{\partial}{\partial x}(\frac{\phi_y g \delta(\phi)}{|\nabla \phi|})h \right]dxdy\
&=\mathcal{L}{g1}+\mathcal{L}{g_2}
\end{aligned} \tag{7.1}
$$
由格林公式:
$$
\oint (Sdx+Rdy) = \iint_{\Omega}(\frac{dS}{dx}-\frac{dR}{dy})dxdy
$$
则式(7.1)中的第一项$\mathcal{L}{g1}$可以转化为:
$$
\begin{aligned}
\mathcal{L}{g1}&=\int_{\Omega}\left[ \frac{\partial}{\partial x}(\frac{\phi_xg\delta(\phi)h}{|\nabla h|})+\frac{\partial}{\partial y}(\frac{\phi_y g\delta(\phi)h}{|\nabla h|})\right]dxdy\
&=\oint h(g\delta(\phi)\phi_xdy-g\delta(\phi)\phi_ydx)\
&=0\quad (\because h|{\partial\Omega}=0)
\end{aligned}
$$
所以
$$
\begin{aligned}
\frac{\partial \mathcal{L_g}(\phi+\varepsilon h)}{\partial \varepsilon}\bigg |{\varepsilon\rightarrow0}
&=
-\int_{\Omega} \left[ \frac{\partial}{\partial x}(\frac{\phi_x g \delta(\phi)}{|\nabla \phi|})h+\frac{\partial}{\partial x}(\frac{\phi_y g \delta(\phi)}{|\nabla \phi|})h \right]dxdy\
&=-\int_{\Omega}h \text{div}(\frac{\nabla\phi g \delta(\phi)}{|\nabla \phi|})dxdy
\end{aligned} \tag{7.2}
$$
当给定x, y时,$\nabla \phi$是向量,$g, \delta$都是标量,因此:
$$
\begin{aligned}
h\text{div}(\frac{\nabla\phi g \delta(\phi)}{|\nabla \phi|})
&= h\left[ \frac{\nabla \phi}{|\nabla \phi|}\nabla(g\delta(\phi))+\text{div}(\frac{\nabla \phi}{|\nabla \phi|})g\delta(\phi) \right]\
&= h\left[ \frac{\nabla \phi}{|\nabla \phi|}(\nabla g \cdot\delta(\phi)+g\delta'(\phi)\nabla\phi)+div(\frac{\nabla \phi}{|\nabla \phi|})g\delta(\phi) \right]
\end{aligned}
$$
因为$h\frac{\nabla \phi}{|\nabla \phi|}g\delta'(\phi)\nabla\phi=0$,有
$$
h\text{div}(\frac{\nabla \phi g \delta(\phi)}{|\nabla \phi|})=h[\frac{\nabla \phi}{|\nabla \phi|}\nabla g\delta(\phi)+\text{div}(\frac{\nabla \phi}{|\nabla \phi|})g\delta(\phi)]=h\delta(\phi)\text{div}(\frac{\nabla \phi g}{|\nabla \phi|})
$$
当$\mathcal{L}g$取最小值时,$\frac{\partial \mathcal{L_g}(\phi+\varepsilon h)}{\partial \varepsilon}\bigg |{\varepsilon\rightarrow0}=0$,由于$h$取得是任意函数,所以得
$$
\delta(\phi)\text{div}(\frac{\nabla \phi g}{|\nabla \phi|})=0
$$
再看第二项:
$$
\mathcal{A}{g}=\int\Omega{gH(-\phi)dxdy},H是阶跃函数
$$
令$F(\phi)=gH(-\phi)$,同理进行一个小的偏移量$\varepsilon h$,其中$h$是任意得函数,且
因此: $$ \frac{\partial F(\phi + \varepsilon h)}{\partial \varepsilon}\bigg|_{\varepsilon\rightarrow0}=-gh\delta(\phi) $$
$$ \frac{\partial \mathcal{A}g(\phi + \varepsilon h)}{\partial \varepsilon}\bigg|{\varepsilon \rightarrow0}=-\int_{\Omega}gh\delta(\phi)dxdy $$
当$\mathcal{A}_g$取最小值时,有$\frac{\partial \mathcal{A}g(\phi + \varepsilon h)}{\partial \varepsilon}\bigg|{\varepsilon \rightarrow0}=0$,由于$h$为任意函数,故: $$ g\delta(\phi)=0 $$
综合式(10)和式(16),可以导出水平集的演化方程为: $$ \frac{\partial \phi}{\partial t}=\lambda\delta(\phi)\text{div}(g\frac{\nabla\phi}{|\nabla\phi|})+\nu g\delta(\phi) $$
2. 基于水平集的图像分割
任务:利用如下演化方程,用matlab代码实现图像分割: $$ \frac{\partial \phi}{\partial t}=\mu[\Delta\phi - \text{div}(\frac{\nabla\phi}{|\nabla \phi|})]+\lambda\delta(\phi)\text{div}(g\frac{\nabla\phi}{|\nabla \phi|})+\nu g\delta(\phi)\ g = \frac{1}{1+|\nabla G_\sigma * I|^2},\quad \delta_{\varepsilon}(x)= \left{ \begin{array}{lr} 0, & |x| \gt \varepsilon \ \frac{1}{2\varepsilon}[1+cos(\frac{\pi x}{\varepsilon})], & |x| \le \varepsilon \end{array} \right. $$
2.1 原理
一个曲面的能量可以由以下变分能量函数进行定义: $$ \varepsilon(\phi)=\mu \mathcal{P}(\phi)+\varepsilon_{g, \lambda, \nu}(\phi) $$ 其中 $$ \mathcal{P}(\phi) = \int_\Omega \frac{1}{2}(|\nabla \phi-1)^2dxdy\ \varepsilon_{g,\lambda,\nu}(\phi) = \lambda\mathcal{L}(\phi)+\nu\mathcal{A}g(\phi) $$ $\mathcal{P}$限制曲面尽可能光滑(类似于正则项),$\varepsilon{g, \lambda, \nu}$限制曲面尽可能向边缘处逼近,通过这两项的权衡,找到使得形成这个平面最小的能量函数对应的曲面。
2.2 各项物理含义
要在提供的水平集代码基础上修改,首先需要理清式(18)中各项的物理含义。
$\phi$
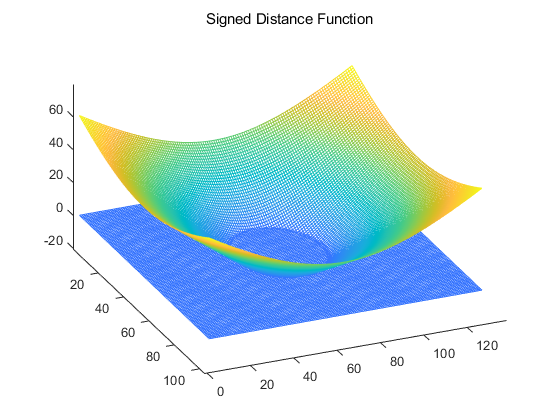
首先来看变量$\phi$,这是定义的符号距离函数。
$$
\phi(x, t)=
\left{
\begin{array}{lr}
< 0, & x \in \Omega \
= 0, & x \in \partial \Omega \
> 0, & x \notin \Omega
\end{array}
\right.
$$
其中,t表示时间, x是水平集设计变量,
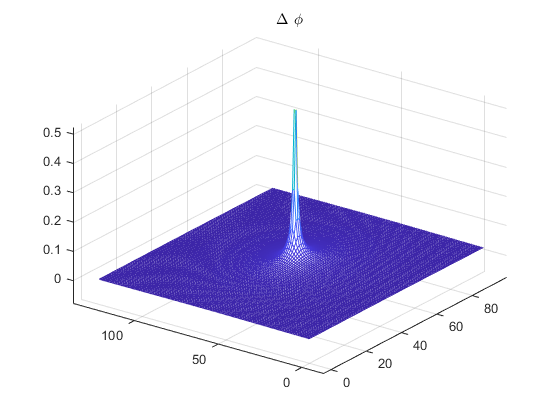
$\Delta \phi$
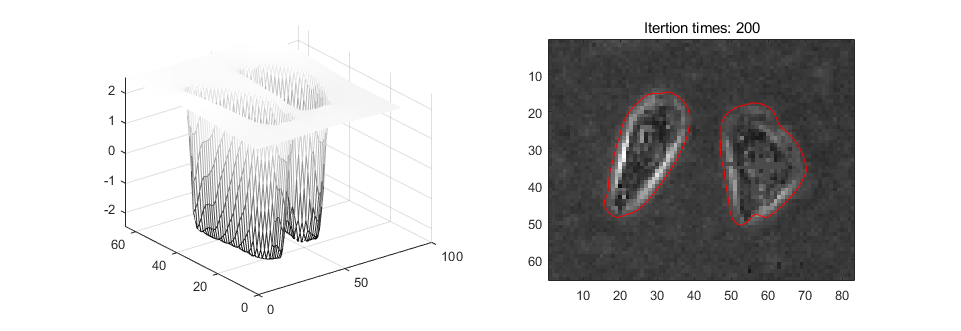
将$\phi$进行拉普拉斯操作,得到结果如下图所示:
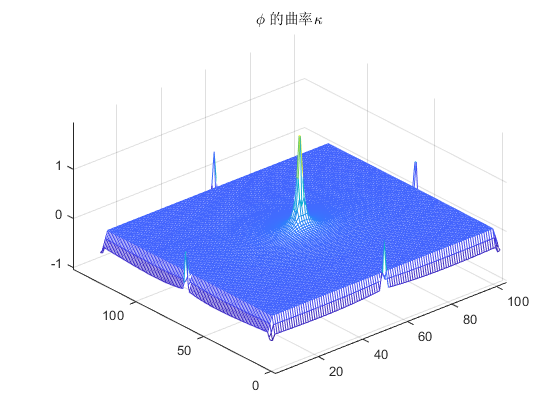
$\text{div}(\frac{\nabla\phi}{|\nabla \phi|})$
$\delta (\phi)$
狄拉克算子,在此演化算法中取近似: $$ \delta_{\varepsilon}(x)= \left{ \begin{array}{lr} 0, & |x| \gt \varepsilon \ \frac{1}{2\varepsilon}[1+cos(\frac{\pi x}{\varepsilon})], & |x| \le \varepsilon \end{array} \right. $$
$g$
2.3 代码实现
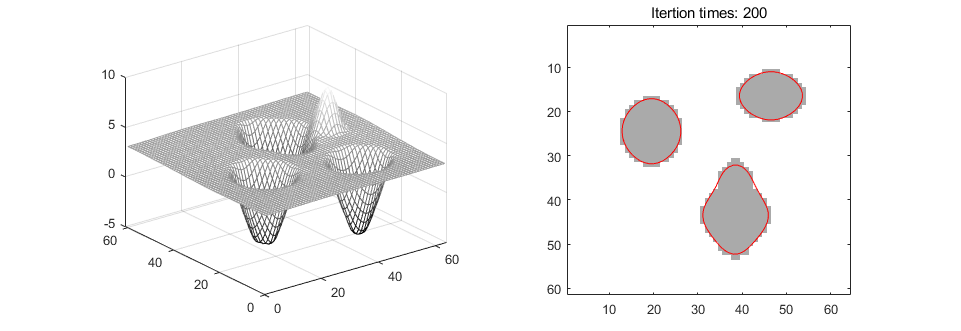
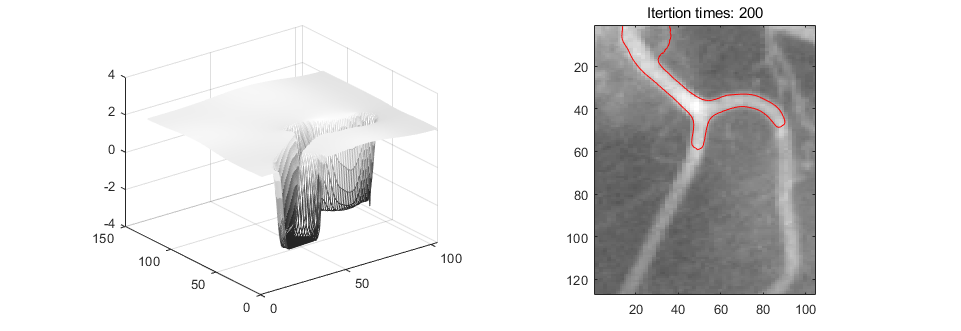
比较Active contours without edges模型与此模型演化函数的异同,仅修改主函数Test_demo和演化函数evolution_cv,就可以实现 Level Set Evolution Without Re-initialization的模型。
代码:
主函数入口为:main.m
需要变更的主要函数为演化方程,即实现: $$ \phi^{t+1} =\phi^{t}+ \frac{\partial \phi}{\partial t}=\phi + \mu[\Delta\phi - \text{div}(\frac{\nabla\phi}{|\nabla \phi|})]+\lambda\delta(\phi)\text{div}(g\frac{\nabla\phi}{|\nabla \phi|})+\nu g\delta(\phi) $$ 虽然实现这一部分不难,但是很难进行参数的调节使得曲面演化完美,因此不得不采用作者论文中的部分code,实现结果如下图所示。可以看出,其对前两图的分割效果较好,第三者可能是由于初始符号函数的选择问题以及参数设置问题,分割效果并不是很好。