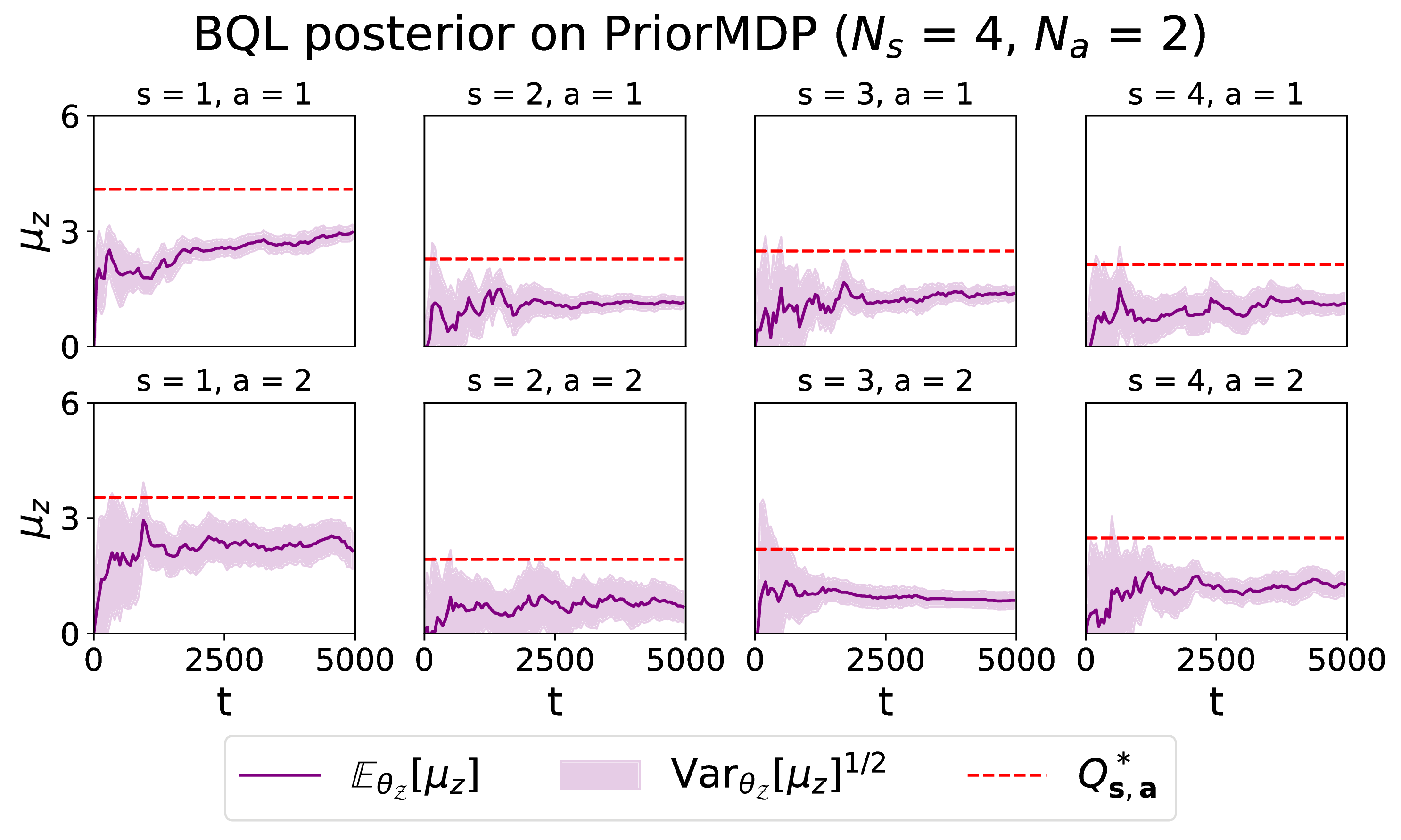
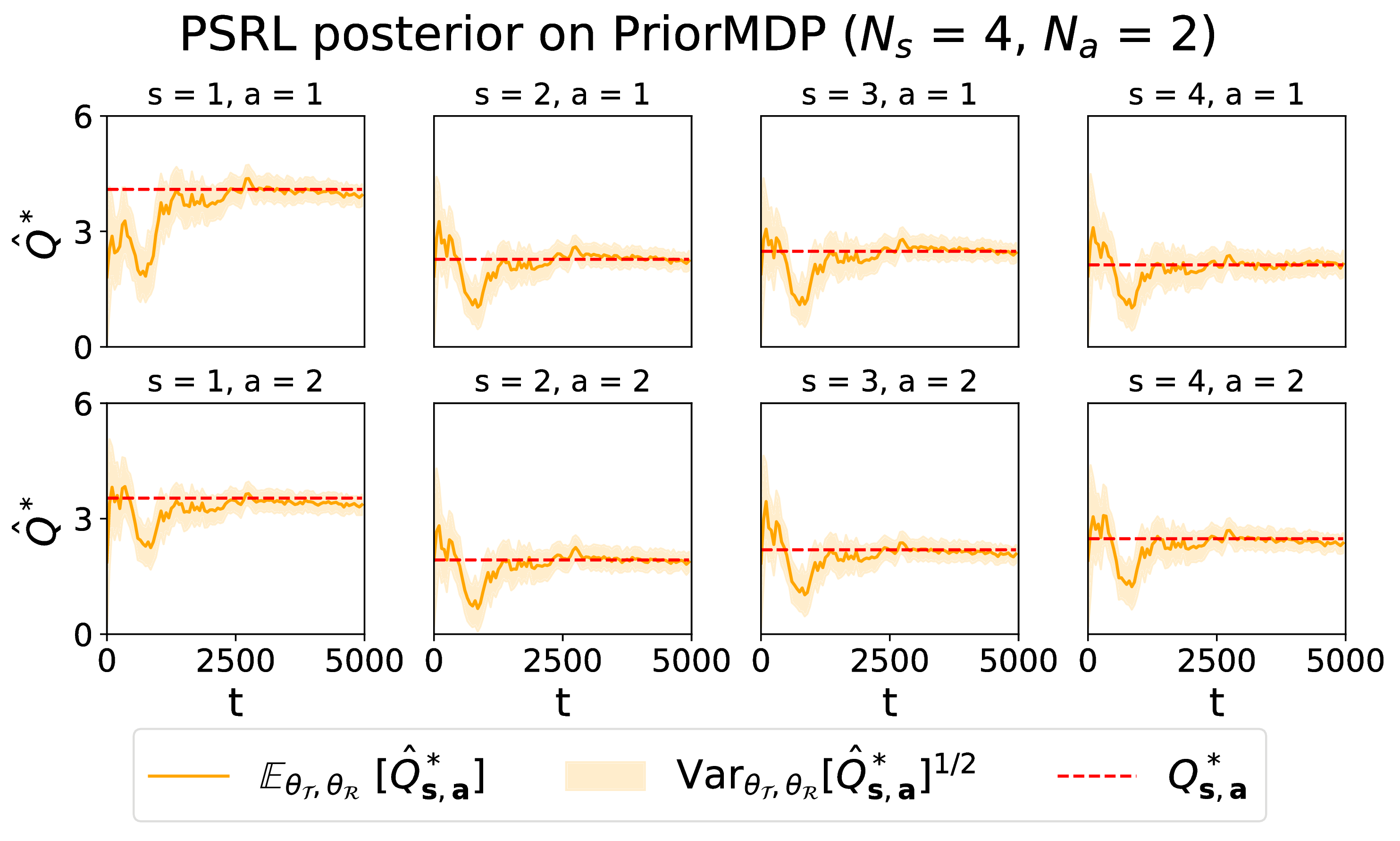
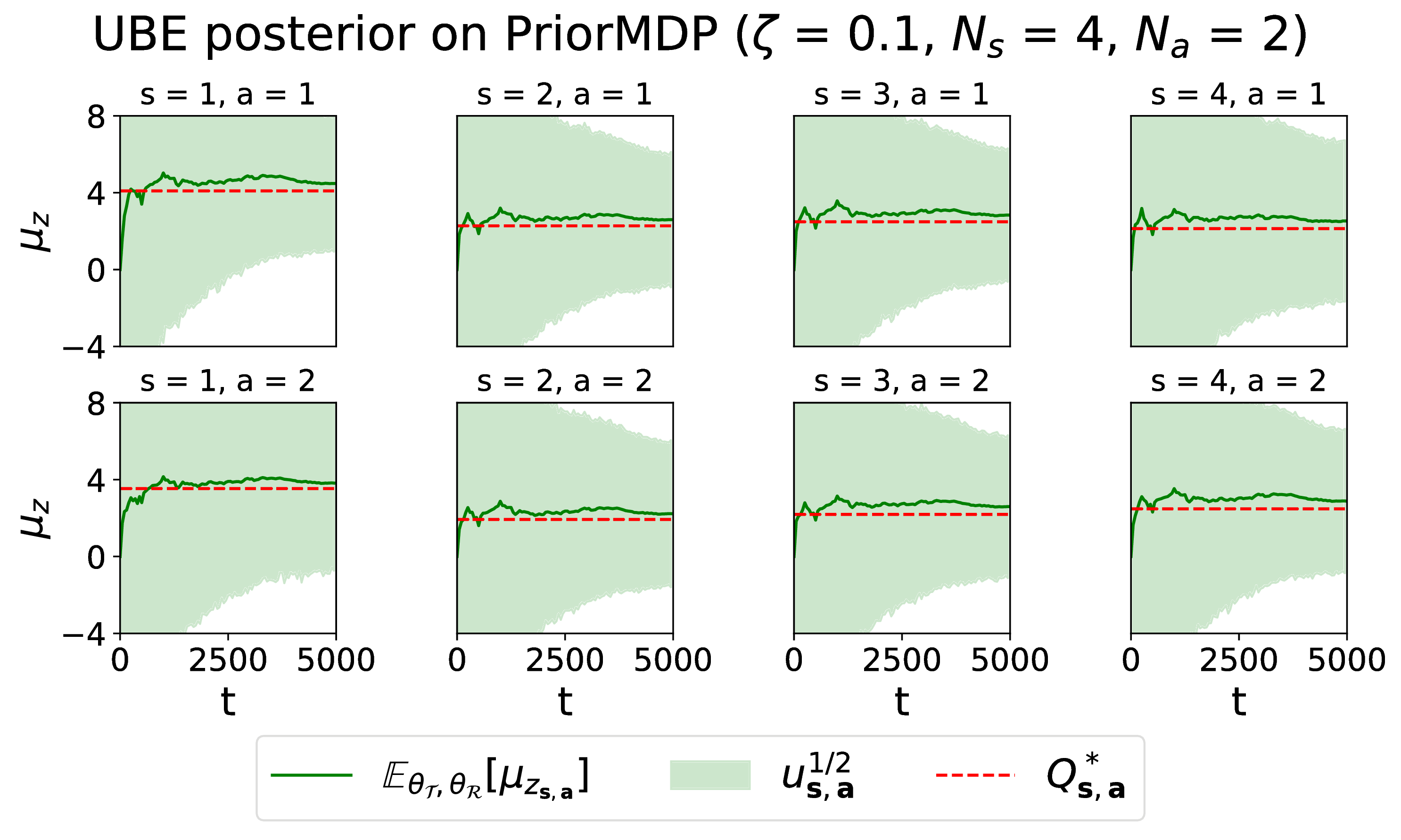
We compare different Bayesian methods for representing an RL agent's uncertainty about cumulative rewards, including our own approach based on moment matching across the Bellman equations.
| Method | Authors | Paper |
|---|---|---|
| Bayesian Q-Learning | Dearden et. al. | link |
| Uncertainty Bellman Equation | O'Donoghue et. al. | link |
| Posterior Sampling for Reinforcement Learning | Osband et. al. | link |
| Moment Matching | Ours | link |
This repository is structured as follows:
writeup/bayesian-methods-for-rl.pdfis the paper.code/contains implementations for agents and environments.code/experimentscontains Jupyter notebooks for reproducing all experiments and plots in the paper.
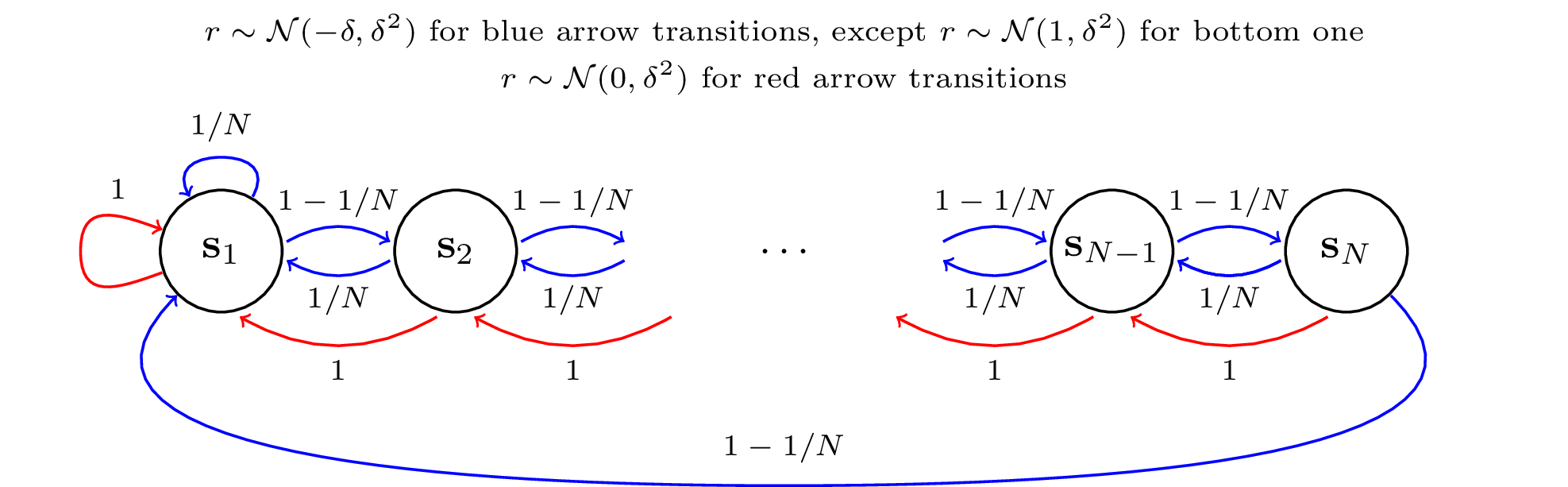
Our DeepSea MDP is a variant of the ones used in Osband et al.. The agent starts from the left-most state and can choose swim-left or swim-right from each of the N states in the environment. Swim-left always succeeds and moves the agent to the left, giving r = 0 (red transitions). Swim-right from s = 1, ..., (N - 1) succeeds with probability (1 - 1/N), moving the agent to the right and otherwise fails moving the agent to the left (blue arrows), giving r ~ N(-δ, δ^2) regardless of whether it succeeds. A successful swim-right from s = N moves the agent back to s = 1 and gives r = 1. We choose δ so that right is optimal for up to N = 40.
This environment is designed to test whether the agent continues exploring despite receiving negative rewards. Sustained exploration becomes increasingly important for large N. As argued in Ian Osband's thesis, in order to avoid exponentially poor performance, exploration in such chain-like environments must be guided by uncertainty rather than randomness.
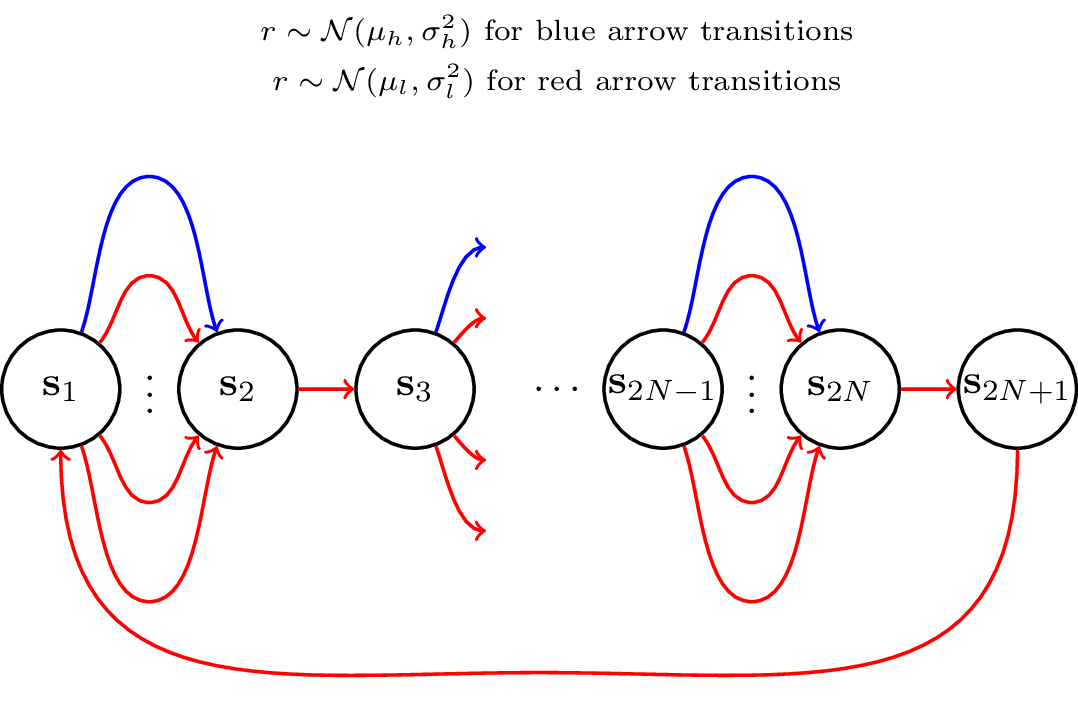
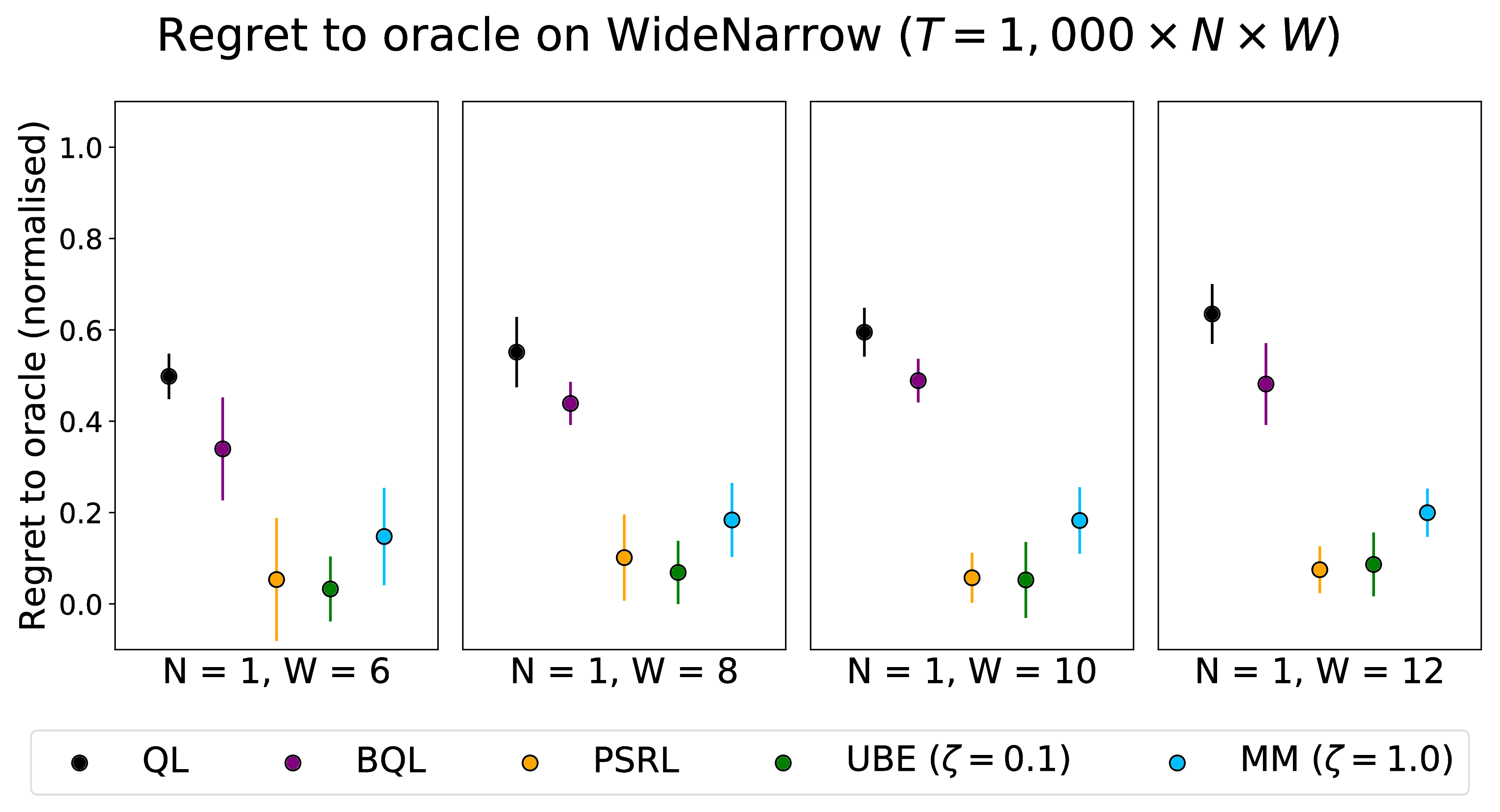
The WideNarrow MDP has 2N + 1 states and deterministic transitions. Odd-numbered states except s = (2N + 1) have W actions, out of which one gives r ~ N(μl, σl^2) whereas all others give r ~ N(μh, σh^2), with μl < μh. Even-numbered states have a single action also giving r ~ N(μh, σh^2). In our experiments we use μh = 0.5, μl = 0 and σl = σh = 1.
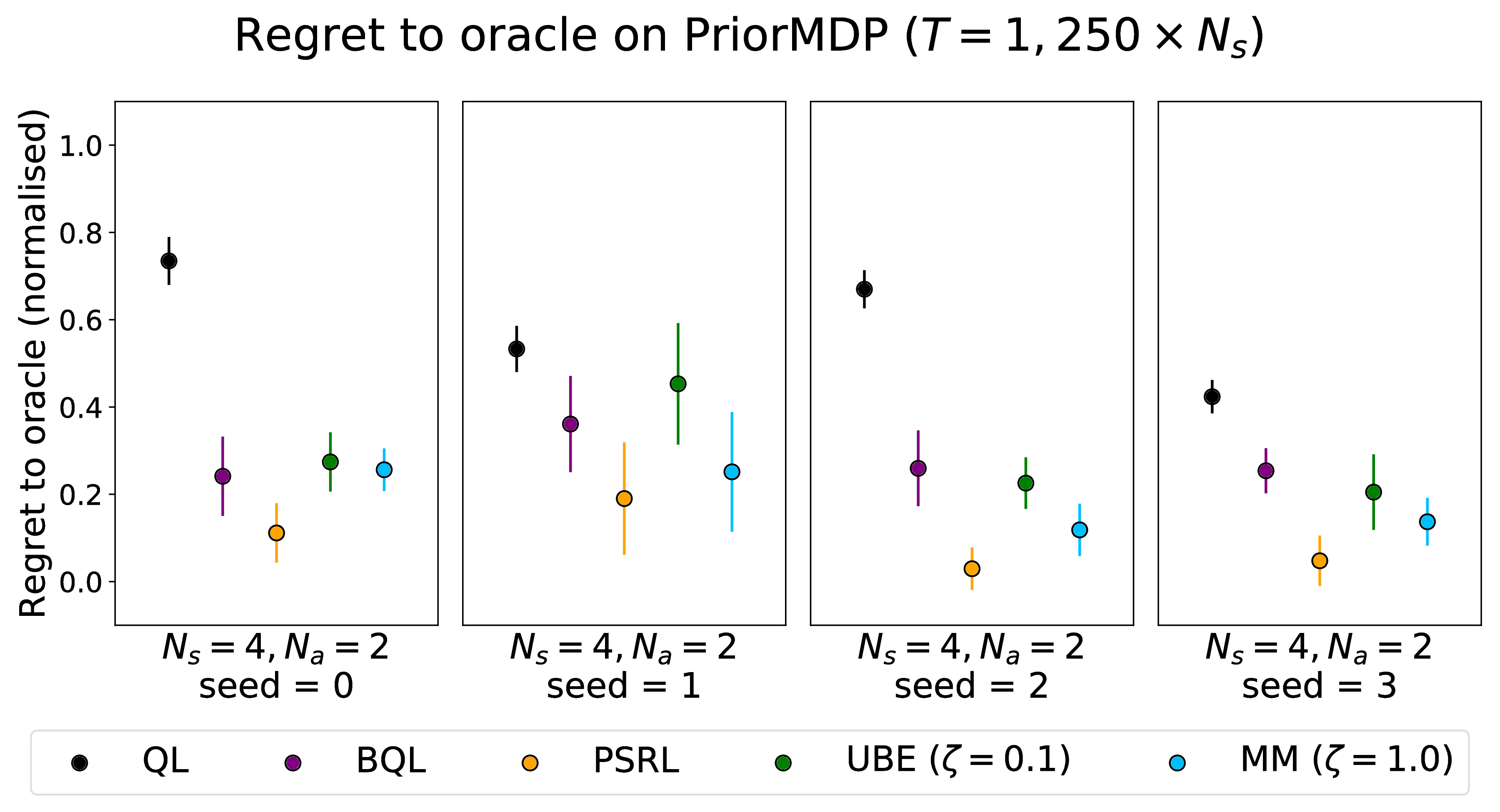
The aforementioned MDPs have very specific and handcrafted dynamics and rewards, so it is interesting to also compare the algorithms on environments which lack this sort of structure. For this we sample finite MDPs with Ns states and Na actions from a prior distribution, as in Osband. The dynamics process s, a -> s' is a separate Categorical for each (s, a), with category probabilities sampled from a Dirichlet prior with concentration κ = 1. The rewards process s, a, s' -> r is a separate Normal for each (s, a, s'), with mean and precision drawn from a Normal-Gamma prior with parameters (μ0, λ, α, β) = (0.00, 1.00, 4.00, 4.00). We chose these hyperparameters because they give Q*-values in a reasonable range.
PSRL performs best in terms of regret, occasionally tied with another method. All Bayesian methods perform better than Q-Learning with ε-greedy action-selection. We also observe:
- For BQL, the posterior may converge to miscalibrated values. If this occurs and the agent converges to a greedy policy that is not the optimal policy, the regret performance becomes very poor. This depends highly on the prior initialisation of BQL.
- For UBE, performance depends highly on tuning the Thompson noise ζ well. If ζ is too large, the agent over-explores and the regret plateaus too slowly, whereas if ζ is too small, the agent takes too many suboptimal actions.
- For MM, although performance is sometimes competitive with PSRL, the factored approximation hurts the regret in other cases, because Thompson sampling for the posterior results in frequent selection of suboptimal actions.
If you use this code or writeup material in your work please cite: E. Markou and C. E. Rasmussen, Bayesian methods for efficient Reinforcement Learning in tabular problems, 2019 NeurIPS Workshop on Biological and Artificial RL.