使用sklearn做特征工程
有这么一句话在业界广泛流传,数据和特征决定了机器学习的上限,而模型和算法只是逼近这个上限而已。那特征工程到底是什么呢?顾名思义,其本质是一项工程活动,目的是最大限度地从原始数据中提取特征以供算法和模型使用。
特征工程主要分为三部分:
- 数据预处理 对应的sklearn包:sklearn-Processing data
- 特征选择 对应的sklearn包: sklearn-Feature selection
- 降维 对应的sklearn包: sklearn-Dimensionality reduction
本文中使用sklearn中的IRIS(鸢尾花)数据集来对特征处理功能进行说明导入IRIS数据集的代码如下:
1 from sklearn.datasets import load_iris
2
3 #导入IRIS数据集
4 iris = load_iris()
5
6 #特征矩阵
7 iris.data
8
9 #目标向量
10 iris.target
通过特征提取,我们能得到未经处理的特征,这时的特征可能有以下问题:
- 不属于同一量纲:即特征的规格不一样,不能够放在一起比较。无量纲化可以解决这一问题。
- 信息冗余:对于某些定量特征,其包含的有效信息为区间划分,例如学习成绩,假若只关心“及格”或不“及格”,那么需要将定量的考分,转换成“1”和“0”表示及格和未及格。二值化可以解决这一问题。
- 定性特征不能直接使用:通常使用哑编码的方式将定性特征转换为定量特征,假设有N种定性值,则将这一个特征扩展为N种特征,当原始特征值为第i种定性值时,第i个扩展特征赋值为1,其他扩展特征赋值为0。哑编码的方式相比直接指定的方式,不用增加调参的工作,对于线性模型来说,使用哑编码后的特征可达到非线性的效果。
- 存在缺失值:填充缺失值。
- 信息利用率低:不同的机器学习算法和模型对数据中信息的利用是不同的,之前提到在线性模型中,使用对定性特征哑编码可以达到非线性的效果。类似地,对定量变量多项式化,或者进行其他的数据变换,都能达到非线性的效果。
我们使用sklearn中的preproccessing库来进行数据预处理。
无量纲化使不同规格的数据转换到同一规格
将服从正态分布的特征值转换成标准正态分布,标准化需要计算特征的均值和标准差,公式表达为:

使用preproccessing库的StandardScaler类对数据进行标准化的代码如下:
1 from sklearn.preprocessing import StandardScaler
2
3 #标准化,返回值为标准化后的数据
4 StandardScaler().fit_transform(iris.data)
区间缩放法的思路有多种,常见的一种为利用两个最值进行缩放,公式表达为:

使用preproccessing库的MinMaxScaler类对数据进行区间缩放的代码如下:
1 from sklearn.preprocessing import MinMaxScaler
2
3 #区间缩放,返回值为缩放到[0, 1]区间的数据
4 MinMaxScaler().fit_transform(iris.data)
1、在后续的分类、聚类算法中,需要使用距离来度量相似性的时候、或者使用PCA、LDA这些需要用到协方差分析进行降维的时候,同时数据分布可以近似为正太分布,标准化方法(Z-score standardization)表现更好。 2、在不涉及距离度量、协方差计算、数据不符合正太分布的时候,可以使用区间缩放法或其他归一化方法。比如图像处理中,将RGB图像转换为灰度图像后将其值限定在[0 255]的范围。
归一化目的在于样本向量在点乘运算或其他核函数计算相似性时,拥有统一的标准,也就是说都转化为“单位向量”。规则为l2的归一化公式如下:
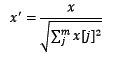
使用preproccessing库的Normalizer类对数据进行归一化的代码如下:
1 from sklearn.preprocessing import Normalizer
2
3 #归一化,返回值为归一化后的数据
4 Normalizer().fit_transform(iris.data)
定性与定量区别
定性:博主很胖,博主很瘦
定量:博主有80kg,博主有60kg
一般定性都会有相关的描述词,定量的描述都是可以用数字来量化处理
定量特征二值化的核心在于设定一个阈值,大于阈值的赋值为1,小于等于阈值的赋值为0,公式表达如下:

使用preproccessing库的Binarizer类对数据进行二值化的代码如下:
1 from sklearn.preprocessing import Binarizer
2
3 #二值化,阈值设置为3,返回值为二值化后的数据
4 Binarizer(threshold=3).fit_transform(iris.data)
因为有些特征是用文字分类表达的,或者说将这些类转化为数字,但是数字与数字之间是没有大小关系的,纯粹的分类标记,这时候就需要用哑编码对其进行编码。IRIS数据集的特征皆为定量特征,使用其目标值进行哑编码(实际上是不需要的)。使用preproccessing库的OneHotEncoder类对数据进行哑编码的代码如下:
1 from sklearn.preprocessing import OneHotEncoder
2
3 #哑编码,对IRIS数据集的目标值,返回值为哑编码后的数据
4 OneHotEncoder().fit_transform(iris.target.reshape((-1,1)))
由于IRIS数据集没有缺失值,故对数据集新增一个样本,4个特征均赋值为NaN,表示数据缺失。使用preproccessing库的Imputer类对数据进行缺失值计算的代码如下:
1 from numpy import vstack, array, nan
2 from sklearn.preprocessing import Imputer
3
4 #缺失值计算,返回值为计算缺失值后的数据
5 #参数missing_value为缺失值的表示形式,默认为NaN
6 #参数strategy为缺失值填充方式,默认为mean(均值)
7 Imputer().fit_transform(vstack((array([nan, nan, nan, nan]), iris.data)))
常见的数据变换有基于多项式的、基于指数函数的、基于对数函数的。4个特征,度为2的多项式转换公式如下:
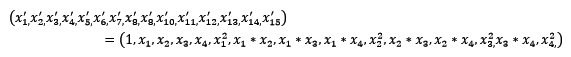
使用preproccessing库的PolynomialFeatures类对数据进行多项式转换的代码如下:
1 from sklearn.preprocessing import PolynomialFeatures
2
3 #多项式转换
4 #参数degree为度,默认值为2
5 PolynomialFeatures().fit_transform(iris.data)
基于单变元函数的数据变换可以使用一个统一的方式完成,使用preproccessing库的FunctionTransformer对数据进行对数函数转换的代码如下:
1 from numpy import log1p
2 from sklearn.preprocessing import FunctionTransformer
3
4 #自定义转换函数为对数函数的数据变换
5 #第一个参数是单变元函数
6 FunctionTransformer(log1p).fit_transform(iris.data)
| 类 | 功能 | 说明 |
|---|---|---|
| StandardScaler | 无量纲化 | 标准化,基于特征矩阵的列,将特征值转换至服从标准正态分布 |
| MinMaxScaler | 无量纲化 | 区间缩放,基于最大最小值,将特征值转换到[0, 1]区间上 |
| Normalizer | 归一化 | 基于特征矩阵的行,将样本向量转换为“单位向量” |
| Binarizer | 二值化 | 基于给定阈值,将定量特征按阈值划分 |
| OneHotEncoder | 哑编码 | 将定性数据编码为定量数据 |
| Imputer | 缺失值计算 | 计算缺失值,缺失值可填充为均值等 |
| PolynomialFeatures | 多项式数据转换 | 多项式数据转换 |
| FunctionTransformer | 自定义单元数据转换 | 使用单变元的函数来转换数据 |
当数据预处理完成后,我们需要选择有意义的特征输入机器学习的算法和模型进行训练。通常来说,从两个方面考虑来选择特征:
- 特征是否发散:如果一个特征不发散,例如方差接近于0,也就是说样本在这个特征上基本上没有差异,这个特征对于样本的区分并没有什么用。
- 特征与目标的相关性:这点比较显见,与目标相关性高的特征,应当优选选择。除方差法外,本文介绍的其他方法均从相关性考虑。
根据特征选择的形式又可以将特征选择方法分为3种:
- Filter:过滤法,不用考虑后续学习器,按照发散性或者相关性对各个特征进行评分,设定阈值或者待选择阈值的个数,选择特征。
- Wrapper:包装法,需考虑后续学习器,根据目标函数(通常是预测效果评分),每次选择若干特征,或者排除若干特征。
- Embedded:嵌入法,是Filter与Wrapper方法的结合。先使用某些机器学习的算法和模型进行训练,得到各个特征的权值系数,根据系数从大到小选择特征。
我们使用sklearn中的feature_selection库来进行特征选择。
使用方差选择法,先要计算各个特征的方差,然后根据阈值,选择方差大于阈值的特征。使用feature_selection库的VarianceThreshold类来选择特征的代码如下:
1 from sklearn.feature_selection import VarianceThreshold
2
3 #方差选择法,返回值为特征选择后的数据
4 #参数threshold为方差的阈值
5 VarianceThreshold(threshold=3).fit_transform(iris.data)
检验特征对标签的相关性,选择其中K个与标签最相关的特征。使用feature_selection库的SelectKBest类结合卡方检验来选择特征的代码如下:
1 from sklearn.feature_selection import SelectKBest
2 from sklearn.feature_selection import chi2
3
4 #选择K个最好的特征,返回选择特征后的数据
5 SelectKBest(chi2, k=2).fit_transform(iris.data, iris.target)
递归消除特征法使用一个基模型来进行多轮训练,每轮训练后,消除若干权值系数的特征,再基于新的特征集进行下一轮训练。使用feature_selection库的RFE类来选择特征的代码如下:
1 from sklearn.feature_selection import RFE
2 from sklearn.linear_model import LogisticRegression
3
4 #递归特征消除法,返回特征选择后的数据
5 #参数estimator为基模型
6 #参数n_features_to_select为选择的特征个数
7 RFE(estimator=LogisticRegression(), n_features_to_select=2).fit_transform(iris.data, iris.target)
使用带惩罚项的基模型,除了筛选出特征外,同时也进行了降维。使用feature_selection库的SelectFromModel类结合带L1惩罚项的逻辑回归模型,来选择特征的代码如下:
1 from sklearn.feature_selection import SelectFromModel
2 from sklearn.linear_model import LogisticRegression
3
4 #带L1惩罚项的逻辑回归作为基模型的特征选择
5 SelectFromModel(LogisticRegression(penalty="l1", C=0.1)).fit_transform(iris.data, iris.target)
树模型中GBDT可用来作为基模型进行特征选择,使用feature_selection库的SelectFromModel类结合GBDT模型,来选择特征的代码如下:
1 from sklearn.feature_selection import SelectFromModel
2 from sklearn.ensemble import GradientBoostingClassifier
3
4 #GBDT作为基模型的特征选择
5 SelectFromModel(GradientBoostingClassifier()).fit_transform(iris.data, iris.target)
| 类 | 所属方式 | 说明 |
|---|---|---|
| VarianceThreshold | Filter | 方差选择法 |
| SelectKBest | Filter | 可选关联系数、卡方校验、最大信息系数作为得分计算的方法 |
| RFE | Wrapper | 递归地训练基模型,将权值系数较小的特征从特征集合中消除 |
| SelectFromModel | Embedded | 训练基模型,选择权值系数较高的特征 |
当特征选择完成后,可以直接训练模型了,但是可能由于特征矩阵过大,导致计算量大,训练时间长的问题,因此降低特征矩阵维度也是必不可少的。常见的降维方法除了以上提到的基于L1惩罚项的模型以外,另外还有主成分分析法(PCA)和线性判别分析(LDA),线性判别分析本身也是一个分类模型。PCA和LDA有很多的相似点,其本质是要将原始的样本映射到维度更低的样本空间中,但是PCA和LDA的映射目标不一样:PCA是为了让映射后的样本具有最大的发散性;而LDA是为了让映射后的样本有最好的分类性能。所以说PCA是一种无监督的降维方法,而LDA是一种有监督的降维方法。
使用decomposition库的PCA类选择特征的代码如下:
1 from sklearn.decomposition import PCA
2
3 #主成分分析法,返回降维后的数据
4 #参数n_components为主成分数目
5 PCA(n_components=2).fit_transform(iris.data)
使用LDA进行降维的代码如下:
1 from sklearn.discriminant_analysis import LinearDiscriminantAnalysis as LDA
2
3 #线性判别分析法,返回降维后的数据
4 #参数n_components为降维后的维数
5 LDA(n_components=2).fit_transform(iris.data, iris.target)
| 库 | 类 | 说明 |
|---|---|---|
| decomposition | PCA | 主成分分析法 |
| lda | LDA | 线性判别分析法 |
注:以上代码均在feature_engineering.py中实现