[TOC]
我们使用以下符号:
-
$A \in \mathbb{R}^{m \times n}$ ,表示$A$ 为由实数组成具有$m$行和$n$列的矩阵。 -
$x \in \mathbb{R}^{ n}$ ,表示具有$n$个元素的向量。 通常,向量$x$将表示列向量: 即,具有$n$行和$1$列的矩阵。 如果我们想要明确地表示行向量: 具有$1$ 行和$n$列的矩阵 - 我们通常写$x^T$(这里$x^T$$x$的转置)。 -
$x_i$ 表示向量$x$的第$i$个元素
- 我们使用符号
$a_{ij}$ (或$A_{ij}$,$A_{i,j}$等)来表示第$i$ 行和第$j$列中的$A$ 的元素:
- 我们用$a^j$或者$A_{:,j}$表示矩阵$A$的第$j$列:
- 我们用$a^T_i$或者$A_{i,:}$表示矩阵$A$的第$i$行:
- 在许多情况下,将矩阵视为列向量或行向量的集合非常重要且方便。 通常,在向量而不是标量上操作在数学上(和概念上)更清晰。只要明确定义了符号,用于矩阵的列或行的表示方式并没有通用约定。
-
加法
-
减法
3. 乘法
-
矩阵乘法结合律:
$(AB)C = A(BC)$ -
矩阵乘法分配律:
$A(B + C) = AB + AC$ -
矩阵乘法通常不是可交换的; 也就是说,通常$AB \ne BA$。 (例如,假设$ A \in \mathbb{R}^ {m \times n},$
$B \in \mathbb{R}^ {n \times p} $ ,如果$m$和$q$不相等,矩阵乘积$BA$甚至不存在!)
4. 单位矩阵
单位矩阵,$I \in \mathbb{R}^{n \times n}
- 逆矩阵
6. 矩阵转置
矩阵的转置是指翻转矩阵的行和列。
给定一个矩阵:
转置的以下属性很容易验证:
$(A^T )^T = A$ - $ (AB)^T = B^T A^T$
$(A + B)^T = A^T + B^T$
-
回归问题
-
分类问题
-
聚类算法
-
异常检测
-
降维
相当于过滤器
cuda 历史版本 GPU驱动
tao-toolkit 训练SDK
快速搭建基于Python和NVIDIA TAO Toolkit的深度学习训练环境
快速搭建基于TensorRT和NVIDIA TAO Toolkit的深度学习训练
tensorrt 部署的时候优化推理
deepstream 部署SDK
- 例子
model = tf.keras.models.Sequential([tf.keras.layers.Flatten(),
tf.keras.layers.Dense(128, activation=tf.nn.relu),
tf.keras.layers.Dense(10, activation=tf.nn.softmax)])Sequential 定义了神经网络中的层序列。 Flatten 会接受一个正方形并将其转换为一维矢量。 Dense 会添加一层神经元。 Activation 函数会告知各层神经元要执行的操作。选项有很多,但目前只采用以下选项: Relu 实际上意味着,如果 X 大于 0,则返回 X,否则返回 0。它只会将 0 或更大的值传递到网络中的下一层。 Softmax 会接受一组值,并能有效地选择最大的值。例如,如果最后一层的输出是 [0.1, 0.1, 0.05, 0.1, 9.5, 0.1, 0.05, 0.05, 0.05],那么您无需通过排序来获取最大值,它会返回 [0,0,0,0,1,0,0,0,0]。
现在已定义了模型,接下来要做的是构建模型。我们来创建模型,先使用 optimizer 和 loss 函数编译模型,然后使用训练数据和标签训练模型。目标是让模型确定训练数据与其训练标签之间的关系。稍后,您希望模型看到与训练数据类似的数据,然后预测该数据应是什么样的。
请注意,我们使用了 metrics= 参数,这样的话,TensorFlow 可根据已知答案(标签)检查预测结果,从而报告训练准确率。
model.compile(optimizer = tf.keras.optimizers.Adam(),
loss = 'sparse_categorical_crossentropy',
metrics=['accuracy'])
model.fit(training_images, training_labels, epochs=5)
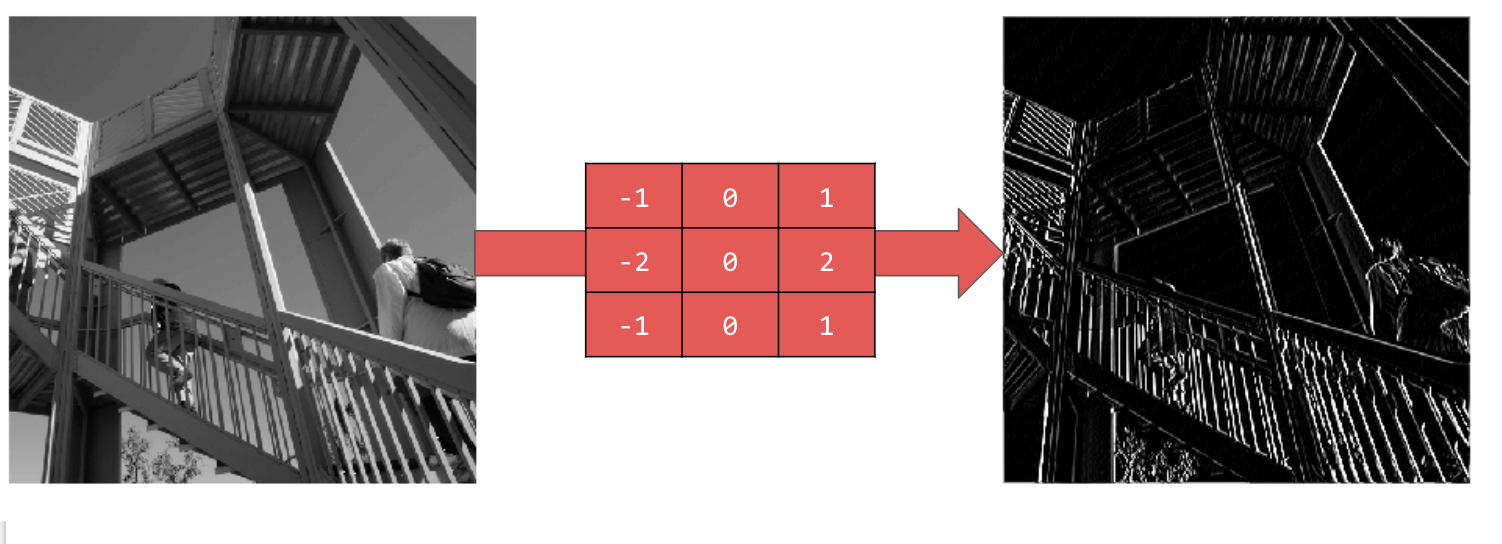
卷积是一种过滤条件,可遍历图片、对其进行处理,然后提取重要的特征。
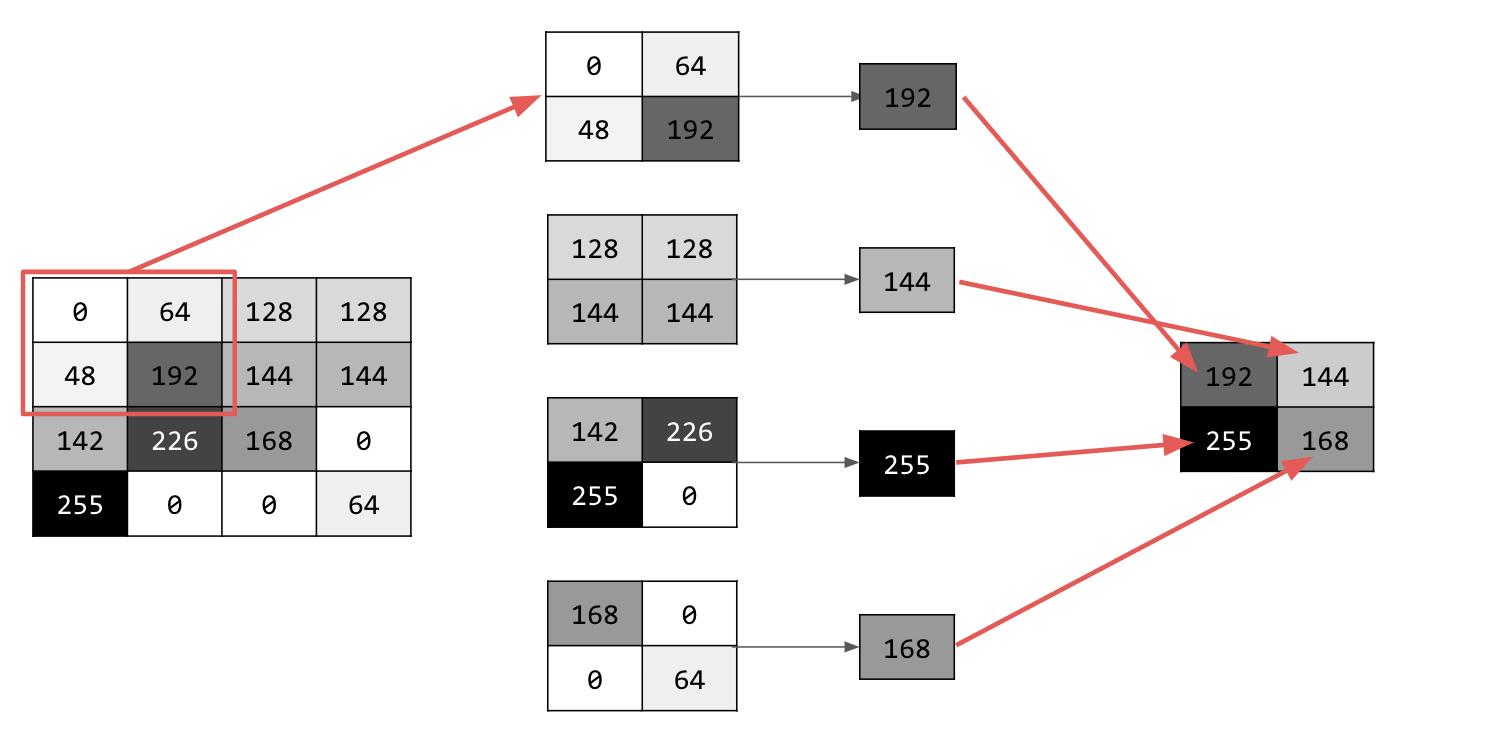
与卷积类似,池化对特征检测有很大帮助。池化层可减少图像中的所有信息量,同时维持检测到的特征。
池化类型有多种,但您可以使用名为“最大池化”的池化类型。
迭代图片,并在每个点上考虑像素及其右侧、下方和右下方直接邻近像素。取其中最大的(即最大池化),并将其加载到新图像中。因此,新图像的大小将是旧图像的四分之一。
import tensorflow as tf
print(tf.__version__)
mnist = tf.keras.datasets.fashion_mnist
(training_images, training_labels), (test_images, test_labels) = mnist.load_data()
# 这是因为第一个卷积需要一个包含所有内容的张量,因此,您只有一个 60000x28x28x1 的 4D 列表,
# 而不是在列表中包含 60000 个 28x28x1 项,测试图像也是如此。否则,您在训练时将收到错误消息,因为卷积无法识别其形状。
training_images=training_images.reshape(60000, 28, 28, 1)
# 归一化
training_images=training_images / 255.0
test_images = test_images.reshape(10000, 28, 28, 1)
# 归一化
test_images=test_images / 255.0
model = tf.keras.models.Sequential([
# 卷积神经 来提取图像特征
tf.keras.layers.Conv2D(64, (3, 3), activation='relu', input_shape=(28, 28, 1)),
# 进行池话 即最大池化
tf.keras.layers.MaxPooling2D(2, 2),
# 卷积神经 来提取图像特征
tf.keras.layers.Conv2D(64, (3, 3), activation='relu'),
# 进行池话 即最大池化
tf.keras.layers.MaxPooling2D(2,2),
# 2维图像 展开成一维图像
tf.keras.layers.Flatten(),
tf.keras.layers.Dense(128, activation='relu'),
tf.keras.layers.Dense(10, activation='softmax')
])
# 编译模型
model.compile(optimizer='adam', loss='sparse_categorical_crossentropy', metrics=['accuracy'])
# 查看网络的大小和形状
model.summary()
# 编译模型,调用拟合方法进行训练,然后评估测试集的损失和准确率。
# 训练模型 训练5次
model.fit(training_images, training_labels, epochs=5)
# 验证模型
test_loss, test_accuracy = model.evaluate(test_images, test_labels)
print ('Test loss: {}, Test accuracy: {}'.format(test_loss, test_accuracy*100))