Aglomera.NET

A hierarchical agglomerative clustering (HAC) library written in C#

Aglomera is a .NET open-source library written entirely in C# that implements hierarchical clustering (HC) algorithms. A cluster refers to a set of instances or data-points. HC can either be agglomerative (bottom-up approach) or divisive (top-down approach). The distance between each instance is calculated using some dissimilarity function. The distance between clusters is calculated using some linkage criterion. Each step of HC produces a new cluster-set, i.e., a set of clusters, from the cluster-set of the previous step.

Agglomerative HC starts with a cluster-set in which each instance belongs to its own cluster. At each step, it merges the two closest clusters, until all clusters have been merged into a single cluster containing all instances, i.e., it ends with a cluster-set containing a single cluster with all instances. Divisive HC works in reverse — it starts by having a cluster-set with one cluster containing all instances. At each step, it splits clusters recursively, using some splitting method, until reaching one cluster-set containing only singletons, i.e., where each instance is placed in its own cluster.

The clustering result is a list containing the cluster-set and the corresponding dissimilarity / distance at which it was created at each step of the algorithm. The result is organized in a hierarchical form, i.e., where each cluster references either the two parents that were merged for its creation (in the agglomerative approach), or the two children resulting from splitting the cluster (in the divisive approach). Due to their hierarchical nature, clustering results can be visualized via a dendrogram.

Currently, Aglomera.NET implements program AGNES (AGglomerative NESting) of [Kaufman & Rousseeuw, 1990], i.e., the bottom-up approach, the It supports different linkage criteria and also provides several metrics to perform internal and external evaluation of clustering results. The results of clustering can be exported to a Json file to be visualized as a dendrogram in Dendrogram Viewer, an interactive web-application using D3.js.

Table of contents

About
API Documentation
Packages and Dependencies
Installation
Features
Examples
See Also

About

Aglomera.NET is open-source under the MIT license and is free for commercial use.

Source repository: https://github.com/pedrodbs/Aglomera
Issue tracker: https://github.com/pedrodbs/Aglomera/issues

Supported platforms:

All runtimes supporting .NET Standard 1.3+ (.NET Core 1.0+, .NET Framework 4.6+) on Windows, Linux and Mac

API Documentation

Packages and Dependencies

The following packages with the corresponding dependencies are provided:

Aglomera: core package, including clustering algorithm, linkage criteria and evaluation metrics.
Aglomera.D3: package to export clustering results to Json files to be visualized with D3.js.
- Json.NET v11.0.2

Installation

You can git clone the Aglomera.NET source code and use an IDE like VisualStudio to build the corresponding binaries.

Getting started

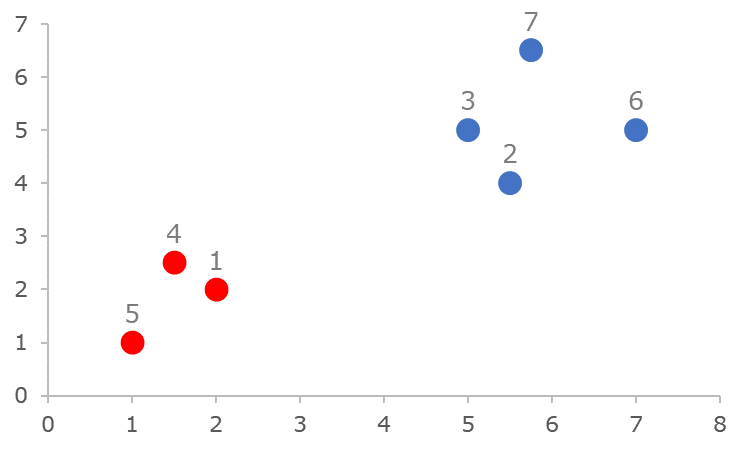
Consider the following data-set example taken from [Kaufman & Rousseeuw, 1990]:

where colors indicate the "real" instance class, i.e., either 'red' or 'blue'.

Start by defining a data-point class, for example one to represent points in a 2D Euclidean space, such as:

class DataPoint : IComparable<DataPoint>
{
    public DataPoint(string id, double x, double y) { ... }
    public int CompareTo(DataPoint other) { ... }
    ...
}

and then define a dissimilarity metric for this type:

class DissimilarityMetric : IDissimilarityMetric<DataPoint>
{
    public double Calculate(DataPoint instance1, DataPoint instance2) { ... }
}

We can then define the data-set by using:

var dataPoints = new HashSet<DataPoint>(
    new[]
    {
        new DataPoint("1", 2.00, 2.00),
        new DataPoint("2", 5.50, 4.00),
        new DataPoint("3", 5.00, 5.00),
        new DataPoint("4", 1.50, 2.50),
        new DataPoint("5", 1.00, 1.00),
        new DataPoint("6", 7.00, 5.00),
        new DataPoint("7", 5.75, 6.50)
    });

We now select a linkage criterion and create the clustering algorithm:

var metric = new DissimilarityMetric();
var linkage = new AverageLinkage<DataPoint>(metric);
var algorithm = new AgglomerativeClusteringAlgorithm<DataPoint>(linkage);

The clustering result is then obtained by simply executing:

var clusteringResult = algorithm.GetClustering(dataPoints);

Enumerating the result (a ClusteringResult<DataPoint> object) yields the following:

[0]	{0.000	{(1), (2), (3), (4), (5), (6), (7)}}
[1]	{0.707	{(2), (3), (5), (6), (7), (1;4)}}
[2]	{1.118	{(5), (6), (7), (1;4), (2;3)}}
[3]	{1.498	{(6), (7), (2;3), (1;4;5)}}
[4]	{1.901	{(7), (1;4;5), (2;3;6)}}
[5]	{2.047	{(1;4;5), (2;3;6;7)}}
[6]	{5.496	{(1;4;5;2;3;6;7)}}

from which we can select the appropriate data-set, e.g., according to the number of clusters, the distance, external criteria, etc.

Features

Supports the following linkage criteria, used to consider the dissimilarity between clusters:
- Complete (farthest neighbor), average (UPGMA), centroid, minimum energy, single (nearest neighbor), Ward’s minimum variance method.
Provides the following external clustering evaluation criteria, used to evaluate the quality of a given cluster-set when each data-point has associated a certain label / class:
- Purity, normalized mutual information, accuracy, precision, recall, F-measure.
- To externally-evaluate the clustering result, start by indicating the class of each data-point, e.g., a char, and an evaluation criterion:
```
var pointClasses = new Dictionary<DataPoint, char>{...};
var criterion = new NormalizedMutualInformation<DataPoint, char>();
```
  The evaluation score of the 5th cluster-set is given by executing:
```
var score = criterion.Evaluate(clusteringResult[5], pointClasses);
```
Provides the following internal clustering evaluation criteria, used to select the optimal number of clusters when no ground truth is available:
- Silhouette coefficient, Dunn index, Davies-Bouldin index, Calinski-Harabasz index, Modified Gamma statistic, Xie-Beni index, within-between ratio, I-index, Xu index, RMSSD, R-squared.
- To internally-evaluate the clustering result, we simply choose an evaluation criterion and calculate the score:
```
var criterion = new SilhouetteCoefficient<DataPoint>(metric);
var score = criterion.Evaluate(clusteringResult[5]);
```
CSV export
- To export the result of clustering to a comma-separated values (CSV) file, we simply do:
```
clusteringResult.SaveToCsv(FILE_PATH);
```
  which would produce a CSV file with the contents of each cluster in the cluster-set of each step of the algorithm, one instance per line.

D3.js export

Export the result of clustering to a Json file that contains the hierarchical structure of the clustering procedure that can be loaded into Dendrogram Viewer to produce a dendrogram, e.g.:

using Aglomera.D3;
...
clusteringResult.SaveD3DendrogramFile(fullPath, formatting: Formatting.Indented);

would produce Json text like the following:

{
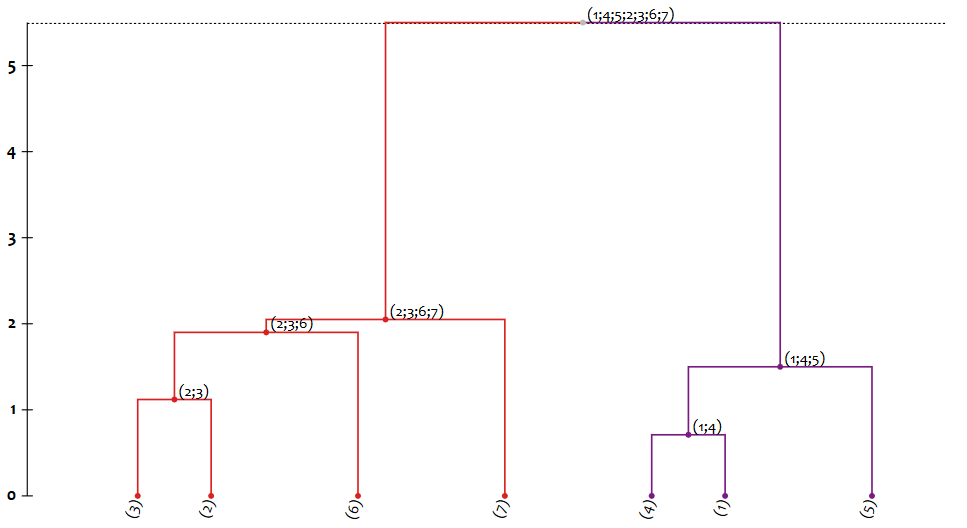
  "n": "(1;4;5;2;3;6;7)", "d": 5.5,
  "c": [
    { "n": "(2;3;6;7)", "d": 2.05,
      "c": [
        {
          "n": "(2;3;6)", "d": 1.9,
          "c": [
            {
              "n": "(2;3)", "d": 1.12,
              "c": [
                { "n": "(3)", "d": 0.0, "c": [] },
                { "n": "(2)", "d": 0.0, "c": [] } ] },
            { "n": "(6)", "d": 0.0, "c": [] } ] },
        { "n": "(7)", "d": 0.0, "c": [] } ]
    },
    { "n": "(1;4;5)", "d": 1.5,
      "c": [
        { "n": "(1;4)", "d": 0.71,
          "c": [
            { "n": "(4)", "d": 0.0, "c": [] },
            { "n": "(1)", "d": 0.0, "c": [] } ] },
        { "n": "(5)", "d": 0.0, "c": [] } ]
    } ]
}

where n holds the name or id of the cluster, d is the dissimilarity / distance at which it was found and created, and c contains the list containing the pair of parents or children of the cluster.

When loaded in Dendrogram Viewer, this would produce the following dendrogram:

Examples

Example code can be found in the src/Examples folder in the repository. Several open-source data-sets adapted to work with the example applications can be found in src/Examples/datasets.

NumericClustering: a simple example of using agglomerative HC to cluster a data-set loaded from an external CSV file. Several linkage criteria are used and clustering results are saved to CSV and D3 Json files.
InternalClusteringEvaluation: shows how to perform evaluation of clustering results using internal criteria. A data-set is loaded from an external CSV file and clustered using agglomerative HC. For each internal criterion, the optimal cluster-set in the clustering result is selected by maximizing the score.
ExternalClusteringEvaluation: shows how to perform evaluation of clustering results using external criteria. A labeled data-set is loaded from an external CSV file and clustered using agglomerative HC. The class of each instance is given by the first character of its id. The score of several external criteria for each cluster-set in the clustering result is then printed to the Console.
ClusteringVisualizer: a Windows.Forms application that allows the visualization of clustering of 2D data. It allows the visual comparison between different linkage criteria and the selection of different number of clusters. Each cluster is attributed a different color according to the selected palette. A screenshot of the application is show below:

lorenzofman/Aglomera