| title |
|---|
Eventual consistency and Alloy |
In Principles of Eventual Consistency (PoEC), Sebastian Burckhardt introduces an approach for reasoning about eventually consistent data types. When it comes to modeling concurrent or distributed algorithms, I've historically looked to TLA+, since it explicitly models time (the "T" is for temporal). Interestingly, Burckhardt's approach doesn't model time explicitly. Instead, the approach uses event graphs, which are defined using sets, relations, and first order logic.
This sounded like a good fit for the Alloy modeling language, which is designed for modeling using sets, relations, and first order logic. This doc is me just playing with some of the concepts in PoEC with Alloy.
Note that this file is written in Alloy Markdown format, so you can load it directly into Alloy 5.0.
Here's an example of how well suited Alloy is to Burckhardt's approach. On page 22 of PoEC, Burckhardt has a table properties of binaries relations, along with their algebraic definitions. Translating from the algebraic definitions to Alloy syntax is very straightforward.
We'll start by defining a macro to represent idA in Alloy:
let id[A] = A<:idenHere are the properties and their direct translation into alloy.
| Property | Algebraic definition | Alloy syntax |
|---|---|---|
| symmetric | rel=rel-1 | rel=~rel |
| reflexive | idA ⊆ rel | id[A] in rel |
| irreflexive | idA ∩ rel = ∅ | id[A] & rel = none |
| transitive | (rel;rel) ⊆ rel | rel.rel in rel |
| acyclic | idA ∩ rel+ = ∅ | id[A] & ^rel = none |
| total | rel ∪ rel-1 ∪ idA = A×A | rel + ~rel + id[A] = A->A |
As our motivating example, we're going to use Alloy to model the behavior of a register. A register is a very simple data structure that holds a single value.
A register supports two operations: read a value and write a value.
We introduce two models of a shared-memory register from the book Introduction to Reliable and Secure Distributed Programming (ItRaSDP) by Cachin, Guerraoui and Rodridgues.
- (1,N) regular register
- (1,N) atomic register
From ItRaSDP (Section 4.2.1, Module 4.1, p143), here's the validity property of a (1, N) regular register:
A read that is not concurrent with a write returns the last value written; a read that is concurrent with a write returns the last value written or the value currently written.
A (1,N) atomic register has the same properties as a (1,N) regular register, and an additional ordering property. From ItRaSDP (Section 4.3.1, Module 4.2, p149):
If a read returns a value v and a subsequent read returns a value w, then the write of w does not precede the write of v.
We'll use alloy to generate an abstract execution for a register. PoEC defines abstract executions in section 3.2 (p34).
An abstract execution is made up of:
- E - set of events
- op - relation that maps events to operations
- rval - relation that maps events to values returned by the operation
- rb - "returns before" relation that captures which operations returned before which other ones
- ss - "same session" relation that captures which operations are part of the same session (you can think of it as a thread or process)
- vis - visibility relation
- ar - arbitration relation
The convention we'll use for return values is:
- For writes, the return value is
OK - For reads, the return value is either a legitimate value, or
Undefif the register has never had a value written before: - If an operation does not complete, the return value is
NeverReturns.
In our alloy model, we'll define an E signature, and op,rval,rb,ss,vis,ar fields to model the relations.
I'd normally call this "Event" instead of "E", but I'll use "E" here to be consistent with Burckhardt's syntax.
sig E {
op: Operation,
rval: Value + NeverReturns,
rb: set E,
ss: set E,
vis: set E,
ar: set E
}Note how the op and rval relations map an event to an individual element of a set, and the other relations map an event to a set of events.
Next, we need to define Operation, Value, Undef, OK.
Value is just a set of values, it's the simplest possible definition of an Alloy signature:
sig Value {}We're going to define V as the values that can be written to the register.
sig V extends Value {}We'll also define Undef and OK, which we model as singleton sets:
one sig Undef extends Value {}
one sig OK extends Value {}Finally, we need to model with Burckhardt refers to as ∇, a special value that represents "NeverReturns".
one sig NeverReturns {}To model operations, we need to model reads and writes.
Writes have an argument, so we need a field on the Write signature that associates a write with a value.
abstract sig Operation {}
sig Read extends Operation {}
sig Write extends Operation {
value: V
}There are a number of constraints we need to enforce on some of the relations. In particular:
- rb (returns-before) is a partial order on E (Definition 3.1, p32).
- ss (same-session) is an equivalence relation on E (Definition 3.1, p32).
- vis (visibility) is an acyclic relation (Definition 3.3, p35).
- ar (arbitration) is a total order (Definition 3.3, p35).
fact ReturnsBeforeIsPartialOrder {
// Partial orders are irreflexive and transitive (Section 2.1.3, p21)
// irreflexive
no id[E] & rb
// transitive
rb.rb in rb
}
fact SameSessionIsAnEquivalenceRelation {
// Equivalence relations are reflexive, transitive, and symmetric (Section 2.1.3, p22)
// reflexive
id[E] in ss
// transitive
ss.ss in ss
// symmetric
ss=~ss
}
fact VisibilityIsAcyclic {
no id[E] & ^vis
}
fact ArbitrationIsTotalOrder {
// total order is partial order and total
// partial order is irreflexive and transitive
// order defintion is in section 2.1.3
// irreflexive
no id[E] & ar
// transitive
ar.ar in ar
// total
E->E in ar + ~ar + id[E]
}We need to constrain the return values so they match the operations.
- A write operation always returns OK
- A read operation returns either an ordinary value, or a special value, Undef, if it has not been intialized with a value.
fact WritesReturnOK {
all w : op.Write | w.rval = OK
}
fact ReadsReturnValuesOrUndef {
all r : op.Read | r.rval in (Value + Undef)
}We also add one last constraint, to capture the semantics of our register: a read always corresponds to the last visible write in arbitration order, or Undef if there is no visible write.
fact ReadLastVisibleWrite {
all r : op.Read |
some (op.Write & vis.r) => r.rval=lastVisibleWrite[r].op.value else r.rval=Undef
}
fun lastVisibleWrite(e: E): lone E {
{w : op.Write | w->e in vis and no ww : op.Write | ww->e in vis and w->ww in ar}
}We don't want Alloy to generate any orphaned Operation instances, so we specify that all operations have to be associated with an event.
fact AllOpsAreAssociatedWithEvents {
all o : Operation | some op.o
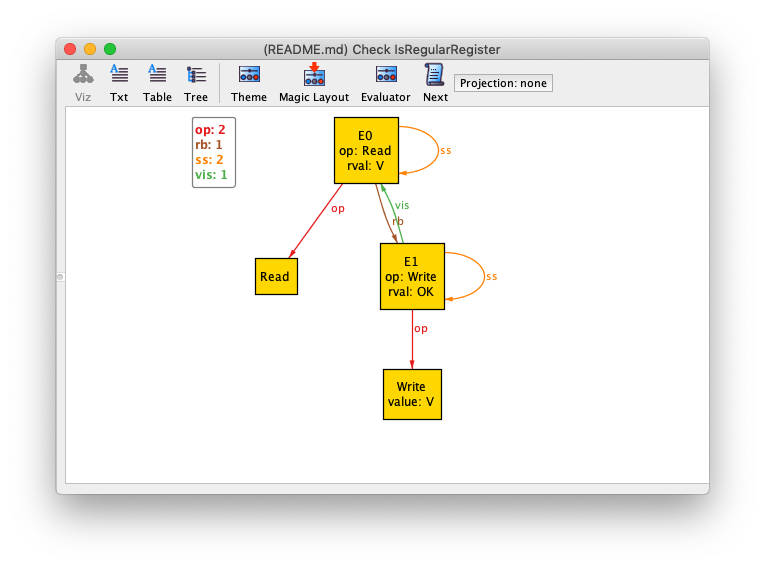
}We can use Alloy to generate an instance of an abstract execution that meets these constraints:
I ran it with these settings:
// Uncomment below to run it
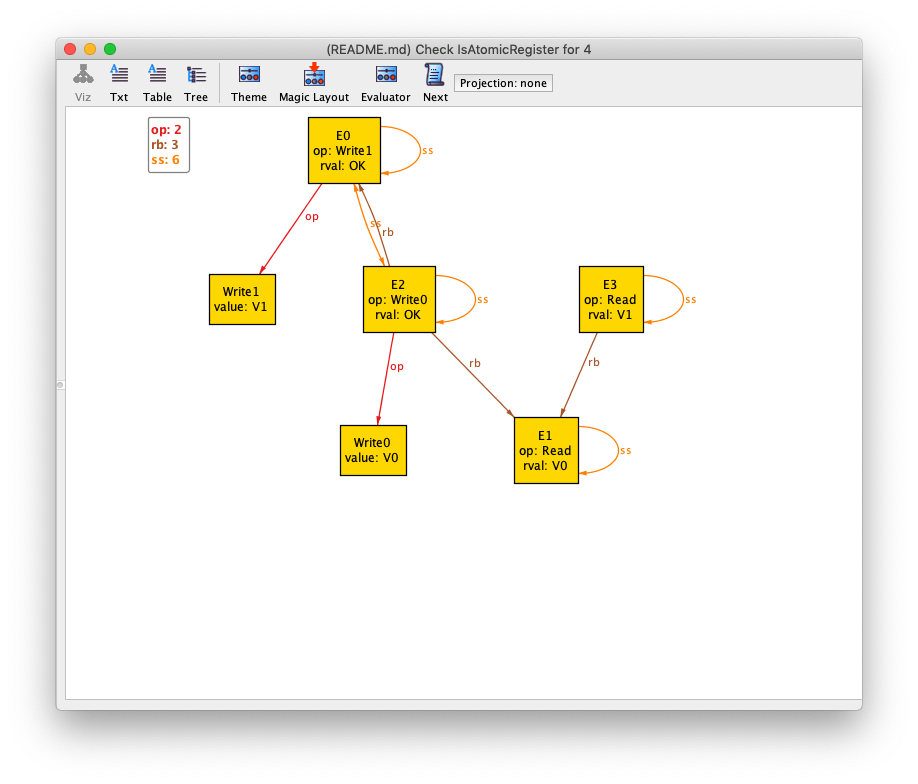
// run {#Read>1 and #Write>1 and some vis} for 4Here's what it generated:
I played with Alloy's theme settings so that the op, rval, and ss fields are shown as attributes.
Let's check if our model satisfies the validity property of a (1,N) regular register.
First, a (1,N) register has only one writer. In the PoEC model, that means all of the writers belong to the same session.
Our model doesn't enforce this, so we need to specify it as a fact:
fact OnlyOneWriter {
all w1,w2: op.Write | w1->w2 in ss
}Next, we assert that the register is regular.
pred RegularRegisterValidity[] {
// A read that is not concurrent with a write returns the last value written
all r : op.Read |
(no w : op.Write | areConcurrent[r,w]) => r.rval = lastValueWritten[r]
// a read that is concurrent with a write returns the last value written or the value currently written.
all r : op.Read |
(some w : op.Write | areConcurrent[r,w]) =>
r.rval in lastValueWritten[r] + {w:op.Write | areConcurrent[r,w]}.op.value
}
// helpers
fun lastValueWrittenWRONG[e : E] : Value { // This is actually wrong, we'll see later
{w : op.Write | (w->e in rb) and (no w2 : op.Write | w2->e in rb and w->w2 in rb)}.op.value
}
// concurrent
fun co[] : E->E {
E->E - (rb + ~rb + id[E])
}
pred areConcurrent[e1,e2 : E] {
e1->e2 in co[]
}
assert IsRegularRegister {
RegularRegisterValidity[]
}
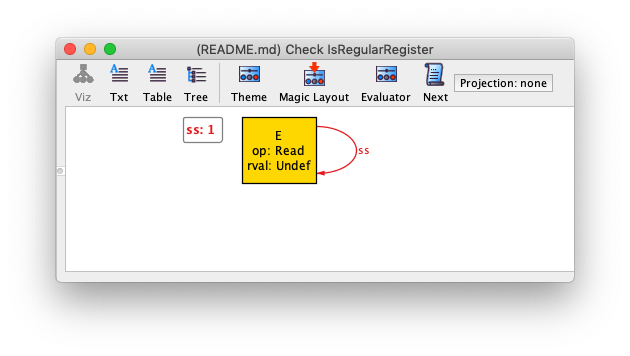
We can then check to see if the register is regular:
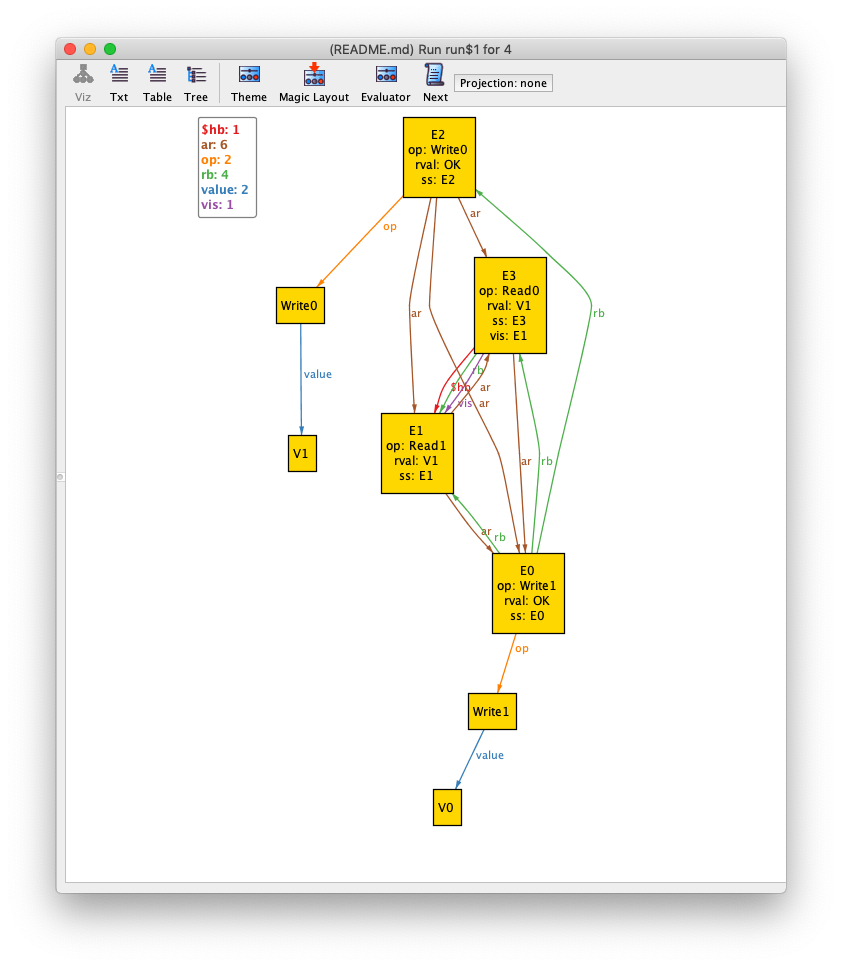
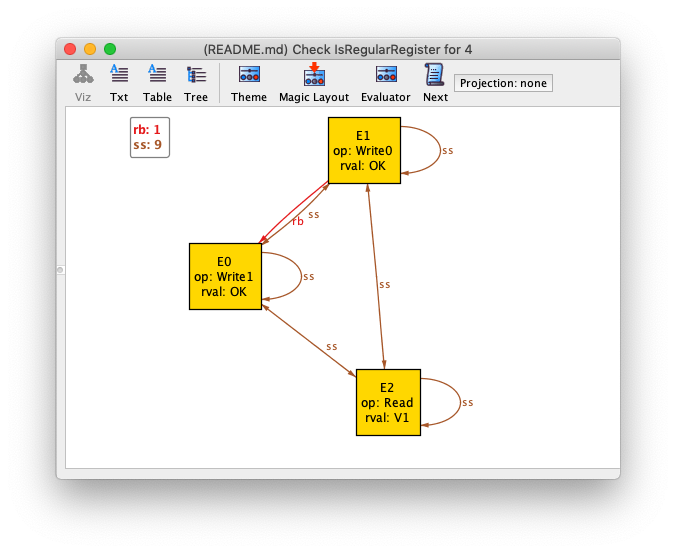
//check IsRegularRegister for 4It fails, with this counterexample:
The problem is that our IsRegularRegister assertion doesn't take into account the case where there hasn't been a write yet.
We need to fix the lastValueWritten function:
fun lastValueWritten[e : E] : Value { // Still wrong! We'll fix this later
let mostRecentWrite = {w : op.Write | (w->e in rb) and (no w2 : op.Write | w2->e in rb and w->w2 in rb)} |
some mostRecentWrite=>mostRecentWrite.op.value else Undef
}Once we do that, and run our check, we get another counterexample:
The problem is that E0 returned before E1, but somehow E0 read E1's write!
The problem is that the vis relationship, which determines write visibility in our model, isn't consistent with causality.
We need to add a restriction to our model. We'll restrict things so writes can't be visible from the future.
fact WritesFromTheFutureAreNeverVisible {
no r,w : E | r in op.Read and w in op.Write and r->w in rb and w->r in vis
}Running it again, we get another counterexample:
Now we have the opposite problem: E1 is a write, E1 returns before E0, and E0 doesn't read the write!
We need to add a restriction that if a write happens before a read, it's visible:
fact WritesThatReturnBeforeReadsAreVisible {
all r : op.Read | all w : op.Write | w->r in rb => w->r in vis
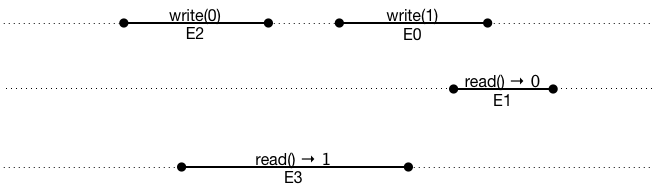
}If we run it again, we get another counterexample. Here's a visualization that shows some of the relationships:
To understand the problem better, here's a timeline graph I manually created with OmniGraffle based on this trace:
Note that E1 reads v0 even though E0 wrote v1.
The problem is that the ar relationship is inconsistent with the rb relationship: E2 is taking effect after E0, even though E0 returned before E2.
We need to specify that the register arbitrates writes consistently with the returns before relation:
fact ArbitrationConsistentWithReturnsBefore {
rb in ar
}If we check again, Alloy finds another counterexample:
Note that E0,E1,E2 are all the same session, but E0 is concurrrent with E2, and E0 is concurrent with E1 (by "concurrent", we mean there's no returns before relationship).
In a real system, in the same session, all events have to be order by the returns before relationship. We missed a constraint.
fact NoConcurrencyInSameSession {
// For any two events, if they are in the samee session, one must return before the other
ss-id[E] in rb + ~rb
}It's not exactly clear what "subsequent" means, so we'll assume it means "returns after"
assert IsAtomicRegister {
// (1,N) atomic registers satisfy (1,N) regular register validity
RegularRegisterValidity[]
// If a read returns a value *v* and a subsequent read returns a value *w*, then the write of *w* does not precede the write of *v*.
no disj w1,w2 : op.Write |
some disj r1,r2 : op.Read, disj v,w : Value | {r1.rval=v r2.rval=w r1->r2 in rb w1.op.value=v w2.op.value=w w2->w1 in rb}
}
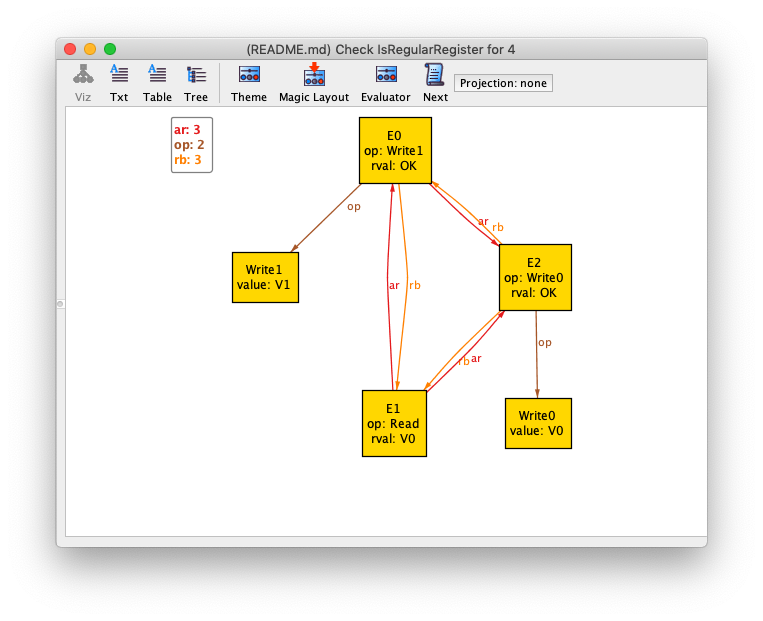
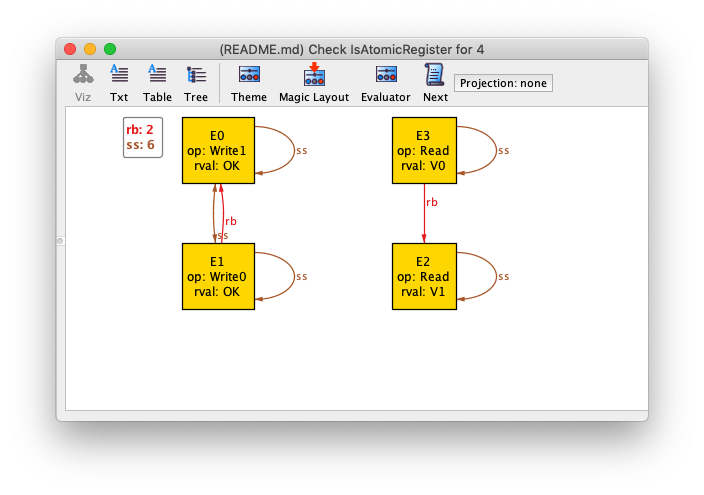
// check IsAtomicRegister for 4Here's the counterexample Alloy comes up with:
Here is what the rb relationship tells us:
- E0 returns before E1
- E3 returns before E2
- E0 is concurrent with E2
- E1 is concurrent with E2
- E0 is concurrent with E3
- E1 is concurrent with E3
If you try to draw this as a timeline, you will find that you can't. Try to make each read overlap both writes without having the writes overlap each other or having the reads overlap each other:
We need a constraint called interval order, from p32 of PoEC:
fact IntervalOrder {
// for all a,b,c,d∈E:(a−→b ∧ c−→d)⇒(a−→d ∨ c−→b).
all a,b,c,d : E | (a->b in rb and c->d in rb) => (a->d in rb or c->b in rb)
}If we run this, we get the following counterexample:
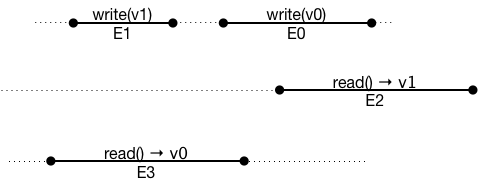
It's easier to understand if redrawn as a timeline:
Here there are three processes: one writer and two readers.
If you look at each read, you can find a write that's either concurrent or happened before, which is consistent with a regular registre.
However, it violates the nature of an atomic register. Note how the writes are ordered (0,1), and how the reads are ordered (1,0). This weirdness is what the atomic register is designed to avoid.
For ordering guarantees, we need to use the ar and vis relationships:
fact VisibilityIsConsistentWithArbitration {
vis in ar
}
fact VisibilityIsConsistentWithReturnsBefore {
rb in vis
}Chapter 5 of PoEC expresses ordering guarantees as predicates on abstract executions. Here's a few of them, with the notation from PoEC in the comments.
assert ReadMyWrites {
// (so ⊆ vis)
so[] in vis
}
assert MonotonicReads {
// (vis ; so) ⊆ vis
vis.so[] in vis
}
assert ConsistentPrefix {
// (ar ; (vis ∩ ¬ss)) ⊆ vis def
ar.(vis-ss) in vis
}
assert NoCircularCausality {
let so = rb & ss |
let hb = ^(so + vis) |
no (id[E] & ^hb)
}
assert CausalVisibility {
hb[] in vis
}
assert CausalArbitration {
hb[] in ar
}
assert RealTime {
rb in ar
}
assert SingleOrder {
// ∃E' ⊆rval (∇):vis=ar\(E'×E)
some E' : set rval.NeverReturns | vis = ar - (E'->E)
}
//
// convenience functions
//
// session order
fun so[]: E->E {
rb & ss
}
// happens before
fun hb[]: E->E {
^(so[] + vis)
}The single order guarantee is tricky because it's expressed in higher-order logic. In general, Alloy can't handle higher-order expressions. IF we try to check the expression above, we'll get the error:
Analysis cannot be performed since it requires higher-order
quantification that could not be skolemized.
What we can do instead is restrict our executions to ones where all operations complete
fact AllOperationsComplete {
no E.rval & NeverReturns
}
// the "C" is for "complete"
assert SingleOrderC {
vis = ar
}We can check the regular register to see which consistency models are violated.
To generate an interesting one, we'll ensure that there are some reads and writes:
To simplify visualization, create an arg function that will show write arguments as an attribute
fun arg[]: E->(V+Undef) {
{e : E, v:(V+Undef) | v=(e in op.Write => e.op.value else Undef)}
}// run {#Read>1 #Write>1 some r : Read | Undef not in (op.r).rval} for 6
fact multipleReadsAndWrites {
#Write>1
#Read>1
Undef not in E.rval
}
check SingleOrderC for 4