lpvcpp/optimal_binary_search_tree

optimal_binary_search_tree

###Dẫn nhập Cây nhị phân là một cấu trúc dữ liệu hết sức quen thuộc với chúng ta. Có rất nhiều nghiên cứu và các thuật toán xoay quanh cấu trúc dữ liệu này. Trong bài viết này, mình xin trình bày về bài toán tối ưu cây nhị phân tìm kiếm (Binary search tree).

Giả sử chúng ta có một cây BST, và đã thực hiện tìm kiếm 1 số lần nào đó trên cây. Sau đó chúng ta nhận ra rằng có một số node nằm ở vị trí khá xa với node root, nhưng lại được tìm kiếm khá thường xuyên. Vậy có cách nào để tái cấu trúc lại cây BST để đưa những node được tìm kiếm thường xuyên về gần với node root hơn, qua đó giảm thiểu chi phí khi tìm kiếm trên cây BST hay không?

Có một cách, đó là tái cấu trúc lại cây BST tùy theo dữ liệu thống kê về số lần tìm kiếm. Chúng ta gọi cây BST đã được tái cấu trúc này là Optimal Binary Search Tree (OBST), có nghĩa là cây nhị phân tìm kiếm tối ưu (NPTKTU).

Bài toán

Input: Cho một tập K = { k₁, k₂, ..., k_n } , là một tập hợp n key phân biệt đã sắp xếp với thứ tự k₁ < k₂ < ... < k_n . Với mỗi key k_i có một xác suất tìm kiếm tương ứng p_i cho key k_i. Tuy nhiên có cả các trường hợp tìm kiếm không thành công. Ví dụ tìm kiếm với một giá trị bất kỳ nhỏ hơn k₁.

Ta gọi tập các giá trị d₀, d₁, d₂, ..., d_n là các giá trị dummy mà thể hiện cho thao tác tìm kiếm các giá trị không nằm trong tập K cho trước. Có nghĩa là d₀ sẽ thể hiện cho các giá trị nhỏ hơn k₁, d₁ thể hiện cho các giá trị lớn hơn k₁ nhưng nhỏ hơn k₂. Với mỗi key dummy d_i, ta có một xác suất tìm kiếm q_i tương đương.

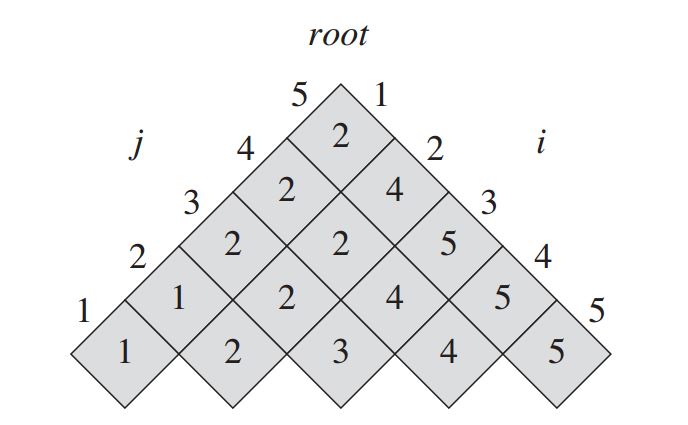
Để dễ hiểu hơn, các bạn có thể tham khảo hình sau:

Lưu ý: Trên thực tế, cây OBST ko hề có các node dummy d_i, tại các vị trí đó vẫn chỉ là các null pointer, tuy nhiên để minh họa dễ hiểu thì các bạn thấy như hình trên.

Trong hình hiển thị ra một tập K có 5 phần tử, và các giá trị key dummy từ d₀ đến d₅.

Ta giả sử số lần tìm kiếm với các key như sau:

• k₁: 15 lần
• k₂: 10 lần
• k₃: 5 lần
• k₄: 10 lần
• k₅: 20 lần
• d₀: 5 lần
• d₁: 10 lần
• d₂: 5 lần
• d₃: 5 lần
• d₄: 5 lần
• d₅: 10 lần

Tổng số lần tìm kiếm là 100, như vậy ta có bảng xác suất tìm kiếm tương ứng như sau:

Như vậy ta có (1):

Tính tổng chi phí tìm kiếm

Vấn đề tiếp theo cần khảo sát là làm sao tính toán được chi phí đối với một cây BST T nào đó khi đã có tập các xác suất tìm kiếm pi và qi đã cho. Để tính toán chi phí này, ta giả sử rằng chi phí tìm kiếm một key bằng với số node phải duyệt qua để tìm được key đó (hoặc là dummy key), tức là tương đương với độ sâu (depth) của node đó cộng thêm 1.

Xét ví dụ với key BST ở hình 1, để tìm kiếm giá trị key = k₁, ta phải đi qua 2 node là k₂ và k₁ cũng tương đương với độ sâu của key k₁ (depth k₁ = 1) cộng với 1.

Như vậy, tổng chi phí để tìm kiếm đối với một cây BST T sẽ là (2):

Rõ ràng, để tìm kiếm một cây OBST, thì việc vét cạn là điều không thể, vì tổng số cây BST có thể tạo ra từ n phần tử lên tới ~4^n/ n ^1.5

Chính vì vậy, việc áp dụng quy hoạch động là cần thiết. Trong phần tiếp theo, mình sẽ trình bày cách tìm cấu trúc cây OBST bằng phương pháp quy hoạch động.

Cấu trúc của cây OBST

Để tìm ra đặc trưng của cây OBST, chúng ta thử bắt đầu bằng việc quan sát những cây con của cây OBST trước. Vậy ta xét một cây con (subtree) của cây OBST mà chúng ta cần tìm.

Một subtree của OBST phải thỏa mãn điều kiện là chứa các key liên tục từ k_i đến k_j, với 1 <= i <= j <= n. Điều này cũng đồng nghĩa với việc cây OBST sẽ chứa các key dummy d_i-1 đến d_j.

Ta có một nhận xét rằng, nếu một cây OBST T, có một cây con T', thì cây con T' này phải là cây nhị phân tối ưu!

Để chứng minh điều này thì đơn giản nên mình ko giải thích thêm ở đây.

Vậy mục tiêu của chúng ta là cố gắng tìm ra cây tối ưu nhị phân, từ các cây con đã tối ưu.

Xét tiếp với cây con T' chứa các key từ k_i đến k_j. Đã là cây thì phải có root, ta gọi k_r là root của cây T' này, với i<= r <= j. Như vậy lúc này, nhánh trái của subtree T' sẽ chứa các key từ k_i đến k_r-1 (và đi kèm là các dummy key từ d_i-1 đến d_r-1). Tương tự, nhánh phải của subtree T' sẽ chứa các key từ k_r+1 đến k_j( và đi kèm là các dummy key từ d_r đến d_j).

Nhưng còn trường hợp các cây subtree empty thì sao? Giả sử ta chọn r = i, khi đó nhánh bên trái của k_r sẽ chứa các key từ k_i đến k_i-1! Thực tế là nhánh này không hề có một key bất kỳ nào cả, chỉ có chứa duy nhất một dummy key, chính là d_i-1 . Cho nên ta quy ước, một cây con chứa các key từ k_i đến k_i-1 thực tế không có bất kỳ key nào, mà chỉ chứa d_i-1 . Tương tự cho trường hợp ta chọn r = j, khi đó cây con k_j+1 đến k_j chỉ chứa dummy key d_j . Điều này rất quan trọng vì sẽ là một bước trong quá trình giải bằng QHĐ sau này.

Phương pháp đệ quy

Chúng ta tổng quát hóa bài toán là tìm kiếm cây con tối ưu cho một tập key từ k_i đến k_j, với i >= 1 và i-1 <= j <= n. Lưu ý rằng khi j = i -1 thì có nghĩa là cây con chỉ có duy nhất một dummy key d_i-1.

Ta định nghĩa e[i,j] là chi phí tìm kiếm đối với một cây OBST chứa các key từ k_i đến k_j. Tức là ta cần tìm e[1,n].

Trường hợp đơn giản khi j = i - 1, cây con chỉ có duy nhất dummy key d_i-1, như vậy rõ ràng chi phí tìm kiếm trên cây con này sẽ là e[i,i-1] = q_i-1.

Với trường hợp j >= i, ta cần chọn root k_r và tạo các cây OBST cho nhánh trái và nhánh phải.

Tạm ngưng ở đây một chút, giả sử bạn có một cây OBST, bây giờ bạn nối cây OBST này vào một node root nào đó, thì điều gì sẽ xảy ra với tổng chi phí tìm kiếm trên cây OBST đó?

Rõ ràng ta thấy, độ sâu (depth) của mỗi node trên cây OBST sẽ tăng lên một, áp vào công thức tính E[search of cost] (2) ở trên, thì rõ ràng tổng chi phí sẽ tăng lên 1 khoảng tương đương với (3):

Như vậy tổng chi phí của cây OBST với các key từ k_i đến k_j và có root là k_r , sẽ chính là chi phí của cây OBST bên trái + chi phí của cây OBST bên phải + chi phí tìm kiếm root k_r+ chi phí đội lên khi ghép cây con bên trái vào root k_r + chi phí đội lên khi ghép cây con bên phải vào root k_r

Hình dung một cách dễ hiểu tức là khi bạn ghép nhánh bên trái vào root kr, và nhánh bên phải vào root kr, thì bạn cần cộng thêm tổng chi phí đội lên (chính là Wij đó), và cộng với chính chi phí khi tìm kiếm k_r nữa (tức là pr).Vậy ta có công thức sau:

Mặt khác, ta lại có

(Chứng minh dễ dàng) thế nên ta có thể viết lại công thức trên thành ![alt text]

Đây chính là công thức đệ quy, với giả sử rằng ta biết được node root k_r.

Tổng quát hóa, ta có công thức tổng quát để tính e[i,j] như sau (4):

Sau khi có công thức tính cost thì bây giờ, bước tiếp theo sẽ là dùng QHĐ để đi tính các chi phí cho tập các cây con của cây OBST.

Bạn sẽ thắc mắc là tại sao chúng ta phải đi tính chi phí này?

Đó là vi khi tính được e[i,j] tối thiểu của cây con subtree chứa các key từ k_i tới k_j, thì đi kèm với đó chính là giá trị root k_r của cây con. Nếu chúng ta tìm được tất cả các root của các cây con trong trường hợp tối ưu, thì có thể dựa vào đó để xây dựng cây OBST.

Dùng Quy hoạch động để giải

Trong phần này, mình sẽ trình bày cách tính e[i,j] và root node. Nếu các bạn đã hiểu được cách tính tay thì việc cài đặt thuật toán bằng code là cực kỳ dễ dàng.

Tính W[i,j]

Đầu tiên, theo công thức tổng quát ở trên, để tính e[i,j], mình cần tính w[i,j] trước, cho nên mình sẽ tính bảng w[i,j] này đầu tiên.

Dễ dàng thấy được, w[i,i-1] = q_i-1 với 1<= i <= n+1 Với j >= i ta có w[i,j] = w[i,j-1] + p_j + q_j (chứng minh từ (3)) Lần lượt tính theo bảng sau, từ dưới lên trên ta có:

Tính cost e[i,j]

Tương tự tính W, ta dễ dàng tính được các giá trị e[i,i-1] với 1 <= i <= n+1 theo công thức (*): e[i,i-1] = q_i-1

Tiếp theo với các cặp i,j khác, ta cần loop từng giá trị r chạy từ i đến j. Với mỗi giá trị r, ta tính cost e[i,j], sau đó lấy ra giá trị cost nhỏ nhất, đồng thời lưu lại giá trị r tương ứng vào bản root tương ứng. Ở đây, bảng root là bảng lưu lại cá giá trị root của cây con subtree tối ưu.

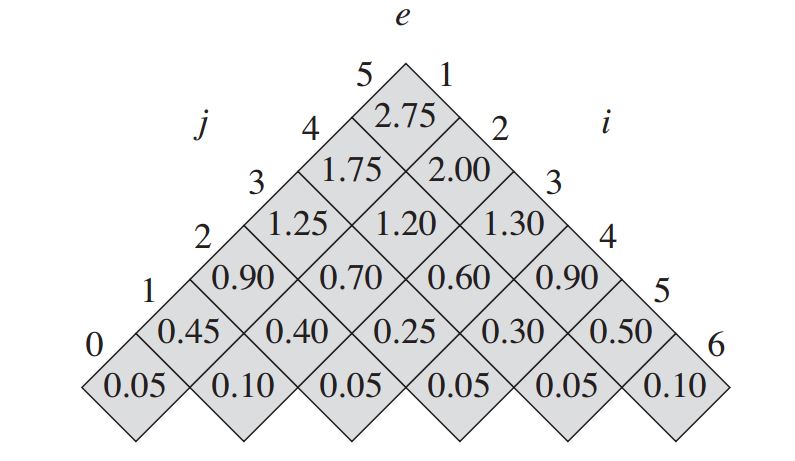
Mình sẽ bắt đầu tính thử để các bạn dễ theo dõi.

• Đầu tiên, ta tính e[1,0], e[2,1], e[3,2], ... , e[6,5]. Tính dễ dàng với công thức (*) ở trên.
• Tiếp theo ta tính e[1,1], tức là cây con chỉ có duy nhất key k₁, theo công thức (4). Trường hợp này, i = j = 1, nên r chỉ có thể có 1 giá trị duy nhất là 1. Ta có: e[1,1] = e[ 1, 0] + e[2,1] +w[1,1] = 0.05 + 0.1 + 0.3 = 0.45 Vì r chỉ có thể có 1 giá trị duy nhất là 1, nên ta lưu r[1,1] = 1 trong bảng root. Tương tự như vậy, ta dễ dàng tính được các giá trị khác là e[2,2], e[3,3]...
• Tiếp theo, ta tính e[1,2], tức là cây con có 2 key k₁ và k₂. Trong trường hợp này, i = 1, j = 2, nên r có thể có 2 trường hợp xảy ra, là r = 1 và r = 2. Đầu tiên, ta xét với r = 1, tính giá trị của e[1,2] theo công thức (4). Sau đó, ta xét r = 2, tính giá trị của e[1,2] theo công thức (4). Giá trị nào nhỏ hơn thì ta lưu lại, đồng thời cập nhật cho bảng root giá trị r[1,2] .

Như vậy tới đây, ta đã tính được bảng root, và từ bảng root, ta có thể xây dựng được cây OBST.

Nhìn vào bảng root ta thấy root [1,5] = 2. Như vậy node root trên cùng chính là k₂

Tiếp đó root[3,5] = 5, có nghĩa là cây con chứa các key k₃, k₄, k₅, sẽ có node root là k₅.

Cứ như vậy lần lượt để xây dựng cây OBST.

Mã giả của chương trình

Cách code khá đơn giản nên mình sẽ không đưa code vào đây. Nếu bạn nào yêu thích có thể tự tìm hiểu hoặc code lại.

Độ phức tạp thuật toán

Cách tính như trên khiến chương trình có độ phức tạo là O(n^3). Tuy nhiên trên thực tế, chúng ta có thể rút ngắn chi phí xuống còn O( n^2) theo cách của D. Knuth.

root[i, j - 1] <= root [i,j] <= root[i+1,j]

Ứng dụng của OBST

• Có thể áp dụng cho các ứng dụng từ điển, với bộ từ vựng là động. Những từ vựng hay được tra, có thể được cấu trúc để đưa lên gần với node root, khi đó chi phí tìm kiếm là rất nhanh, gần như const.
• Ngoài ra, cũng có thể áp dụng cho các bộ định tuyến router, tìm đường đi trên mạng.

Tài liệu tham khảo

1. Thomas H. Cormen. Introduction to algorithms - 3rd Edition
2. Donald E. Knuth. The Art of Computer Programming, Volume 3
3. Donald E. Knuth. Optimum binary search tree

Và cuối cùng, rất cảm ơn nếu các bạn đã đọc tới đây. Trong bài nếu có gì sai sót, rất mong được các bạn chỉ ra, mình xin tiếp thu và sửa chữa nếu cần thiết.

Xin cảm ơn

LePhongVu 11-04-2018