Breadth-first search and depth-first search pathfinder visualizer using regular JavaScript (some jQuery) and HTML canvas.
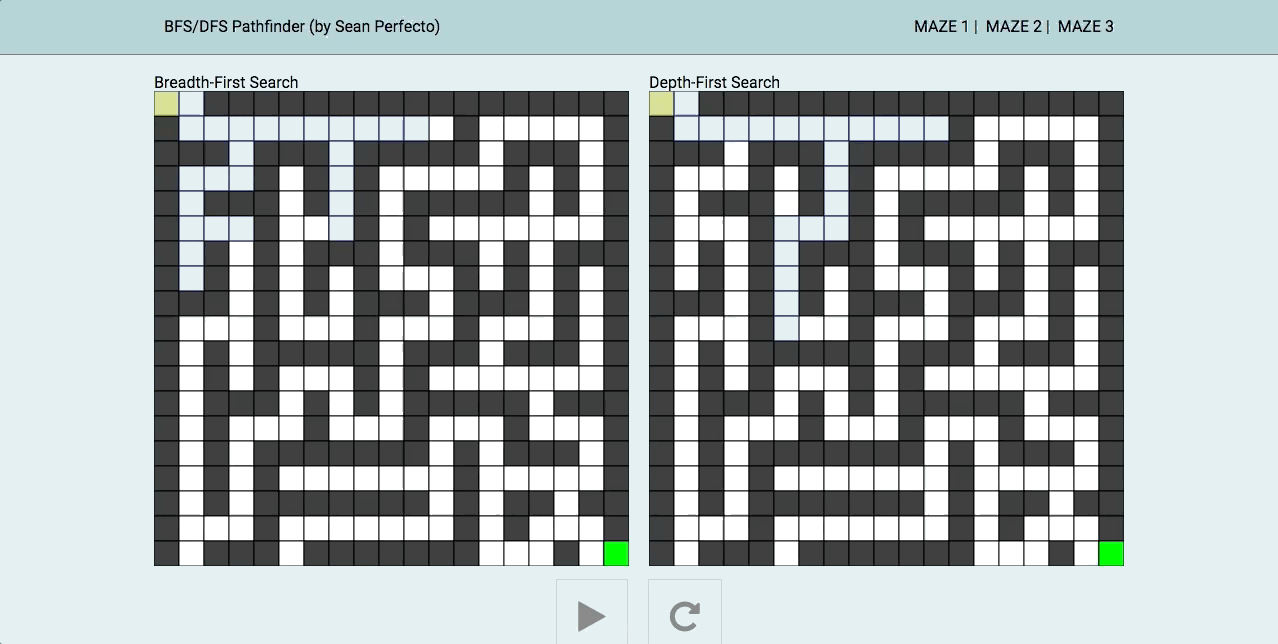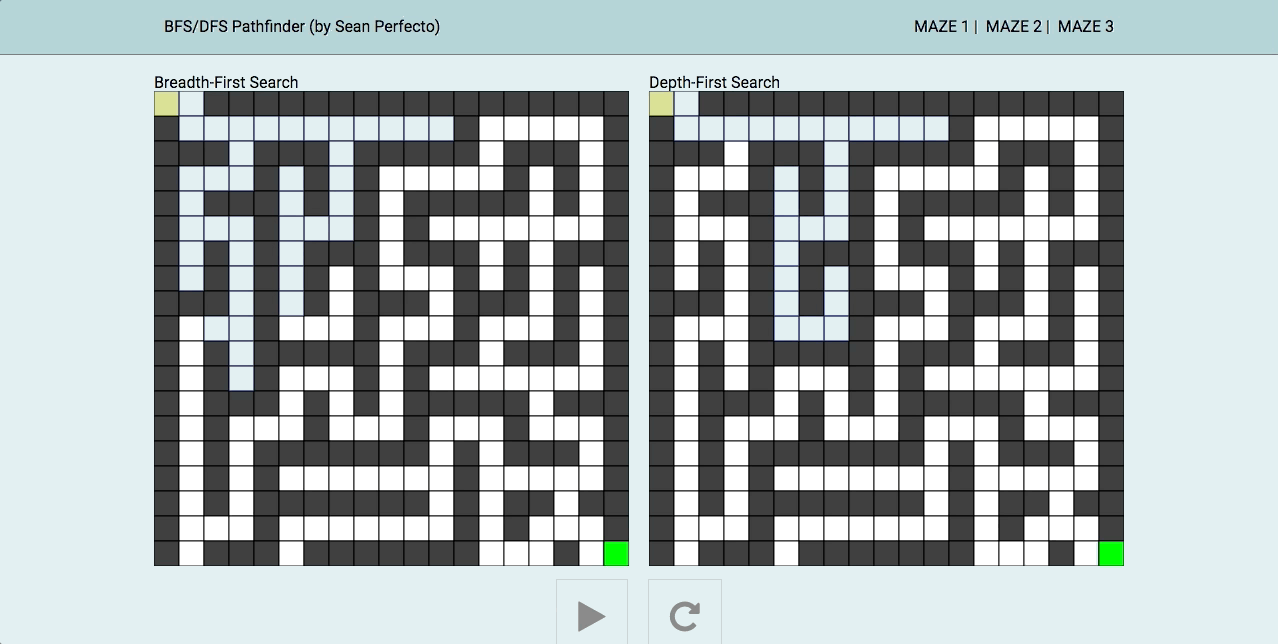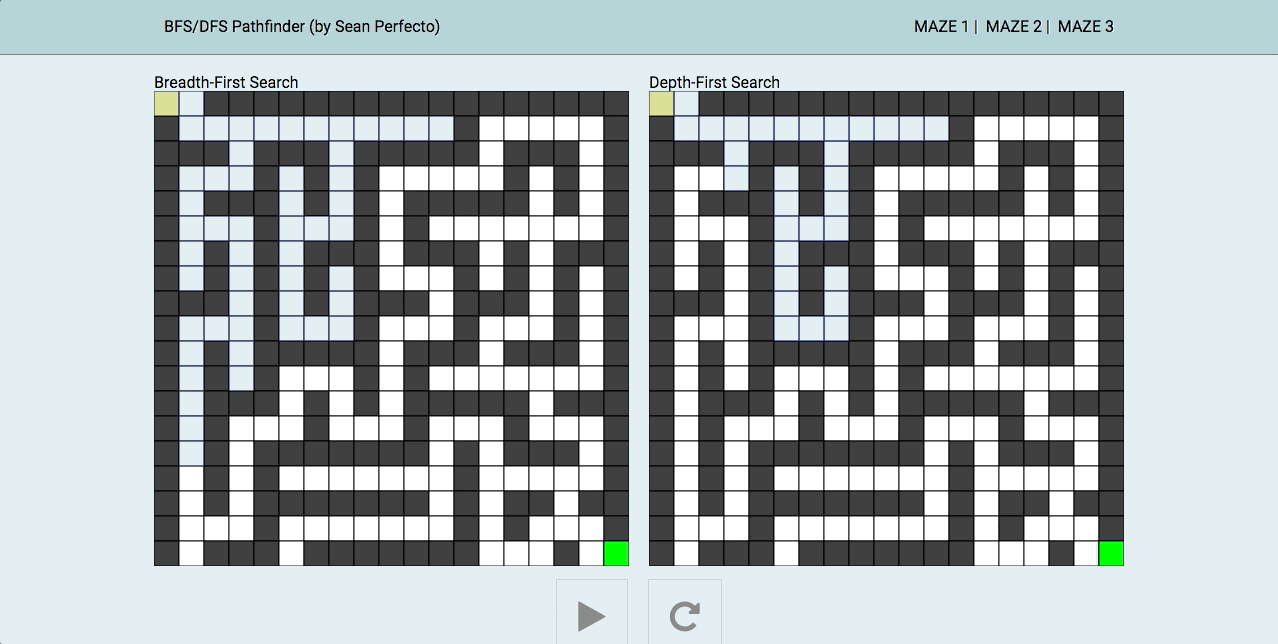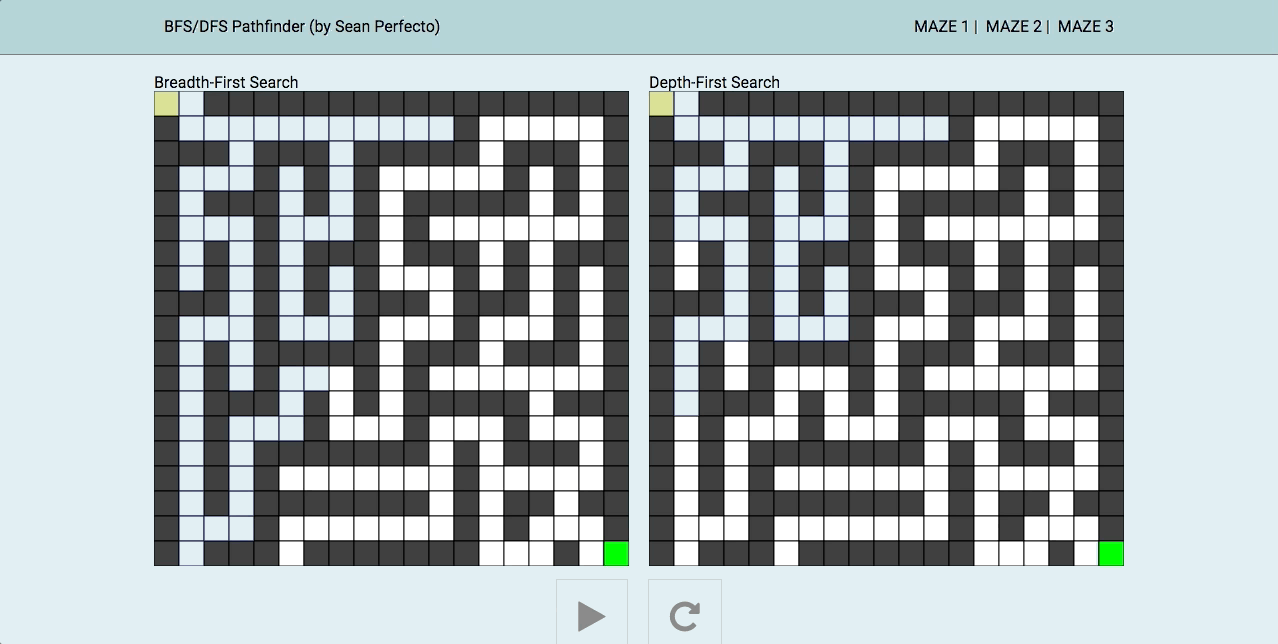
This is a fun project visualizing and comparing two common search algorithms, breadth-first search (BFS) and depth-first search (DFS). Using canvas and implementing the algorithms through JavaScript, the purpose of this project is to see the pathfinding qualities of both side-by-side.
Depending on the type of maze (for example, how far the end position is from the start, types of walls covering), either BFS/DFS has its advantage (as you can see from the three different mazes given).
BFS is an algorithm that start at the starting node and explores its neighbors first, before moving on to their neighbors. My implementation is non-recursive, as it uses a Queue and checks whether the node has been visited or not.
let queue = new Queue();
queue.enqueue(startNode);
cameFrom[startNode.id] = null;
while (true) {
current = queue.dequeue();
current.visited = true;
path.push(current.id);
if (current.id === targetNode.id) {
break;
}
current.adj.forEach((id) => {
if (cameFrom[id]) {
} else {
cameFrom[id] = current.id;
}
let node = getNodeById(graph, id);
if (!node.visited) {
node.visited = true;
queue.enqueue(node);
}
});DFS is different algorithm in that it first starts with the starting node then selects a path and travels that path as far as it can before backtracking. I implemented this non-recursively using a Stack, keeping track of its visited neighbors.
let stack = new Stack();
stack.push(startNode);
cameFrom[startNode.id] = null;
while (true) {
current = stack.top();
path.push(current.id);
current.visited = true;
if (current.id === targetNode.id) {
break;
}
let unvisited = 0;
current.adj.forEach((id) => {
let node = getNodeById(graph, id);
if (!node.visited) {
if (cameFrom[id]) {
} else {
cameFrom[id] = current.id;
}
stack.push(node);
unvisited += 1;
}
});
if (unvisited === 0) {
stack.pop();
}
}- Implement more mazes
- Have it more user interactive, meaning have the user select where to initialize the start and end as well as the walls
- Create mazes that don't have solutions