Fundamentos de Ingeniería Computacional

Laboratorio 1

Implementar un programa que realice lo siguiente:

Debe recibir como entrada un número primo p, de cualquier tamaño (por ejemplo los recomendados para aplicaciones criptográficas (1024,2048,.. bits)
Construir un Grupo multiplicativo $Zp^{\star}$ (usando el conjunto ${1,2,...p-1}$ y la operación ${* mod\ p}$
Usar como generador algún elemento aleatorio de $Zp^{\star}$
Ejecutar el protocolo Diffie Hellman. Se deberá verificar que tanto el valor calculado en A como en B son iguales
Ejecutar en al menos +10 casos de prueba, usando un valor de p diferente para cada caso de prueba
Reportar una tabla de tiempos de ejecución para cada caso de prueba. (Eje X: Nivel de seguridar; Eje Y: Tiempo de ejecución del protocolo Diffie-Hellman)

Inicio

El proyecto está escrito en lenguaje python3.8 (el cual no es muy recomendable para aplicaciones donde se espera un mejor "performance") con ayuda de la libreria pycryptodome

Prerequisitos

Tener la versión >= python3.

Instalar las dependencias marcadas derivadas de sus dependencias bajo los comandos

pip install nombre_paquete

Dependencias

* cryptography = "^38.0.1"
* pycryptodome = "^3.15.0"
* pycryptodomex = "^3.15.0"
* matplotlib = "^3.6.0"
* tabulate = "^0.8.10"

Versión replit

Se cuenta una versión funcional del laboratorio en la plataforma replit. (Se debe de contar con una cuenta) Debido a que es una cuenta gratuita los resultados son limitados, pero funcionales.

https://replit.com/join/syjxpnkjbo-luisballado

Funcionamiento

Se crean dos clases para la creación de una llave a partir del protocolo diffie hellman.

Para dos partes Usuario1 y Usuario2, que intentan establecer una clave secreta el protocolo se implementa como sigue:

Se establece un numero primo p (P) y un generador g (G) que pertenece a la estructura algebraica $Zp^{\star}$ Estos son públicos, conocidos no solo por las partes Usuario1 y Usuario2 sino también por el adversario el canal

Usuario1 escoge $a \in Zp^{\star} - 1$ al azar, y calcula $X = (g^{a}) * mod\ p$ y envia $X$ al Usuario2

Usuario2 escoge $b \in Zp^{\star} - 1$ al azar, y calcula $Y = (g^{b}) * mod\ p$ y envia $Y$ al Usuario1

Nótese que tanto $X$ como $Y$ pueden calcular el valor $K = g^{a*b} * mod\ p$

Como ambas partes pueden calcular $K$, entonces la podemos usar como clave compartida.

Código

Arreglo de bits usados

bits = [1024,1128,1232,1336,1440,1544,1648,1752,1856,1960,2048]

Encapsulamiento del protocolo diffie hellman para ser usado iterativamente para el arreglo de bits y las 31 muestras a tomar Al estar aquí el protocolo, aquí se encuentrá el Grupo Multiplicativo $Zp^{*}$, la obtención del Generador y el intercambio de los valores $x$ & $y$

def diffie_hellman(_bits_):
    P = Crypto.Util.number.getPrime(_bits_,
                                    randfunc=Crypto.Random.get_random_bytes)
    G = (Crypto.Util.number.getRandomRange(1, P - 1)) % P

    cliente1 = UsuarioUno(G, P)
    x = cliente1.__generator__()

    cliente2 = UsuarioDos(G, P)
    y = cliente2.__generator__()

    #print("El valor de X es: " + str(x))
    #print("El valor de Y es: " + str(y))

    key_cliente1 = cliente1.__make_key__(y)
    key_cliente2 = cliente2.__make_key__(x)
    print(comparar_llaves(key_cliente1,key_cliente2))

Clase usuario uno

"""
Clase Usuario Uno
"""
class UsuarioUno:

    def __init__(self, G, P):
        self.g = G
        self.p = P
        self.a = 17

    def __generator__(self):
        self.x = int(pow(self.g, self.a, self.p))

        return self.x

    def __make_key__(self, y):
        self.usuario_uno_key = int(pow(y, self.a, self.p))

        return self.usuario_uno_key

Clase usuario dos

"""
Clase Usuario Dos
"""
class UsuarioDos:

    def __init__(self, G, P):
        self.g = G
        self.p = P
        self.b = 15

    def __generator__(self):
        self.y = int(pow(self.g, self.b, self.p))
        return self.y

    def __make_key__(self, x):
        self.usuario_dos_key = int(pow(x, self.b, self.p))
        return self.usuario_dos_key

creación de gráfica con uso de la libreria matplotlib a partir de los datos generados

def graficar(x_datos,y_datos,result_arr):

  
  print(tabulate(result_arr))
  
  x1 = np.array(x_datos)
  y1 = np.array(y_datos)
  
  plt.plot(x1, y1, marker="o")
  
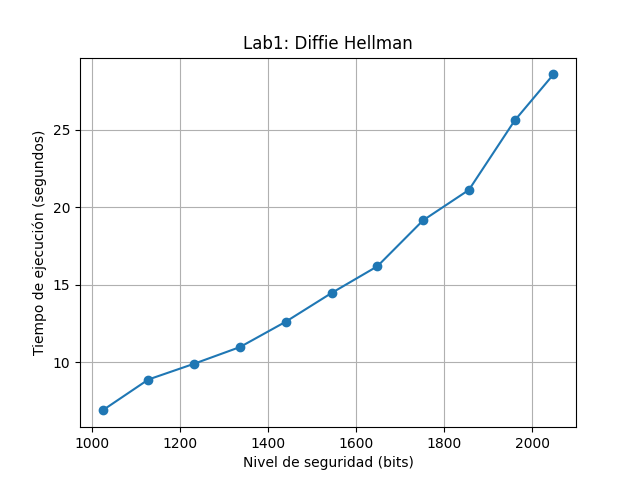
  plt.title("Lab1: Diffie Hellman")
  plt.xlabel("Nivel de seguridad (bits)")
  plt.ylabel("Tiempo de ejecución (segundos)")
  plt.grid()
  plt.show()

comparación de la generación de llaves identicas

def comparar_llaves(self,that):
  if ((self > that) - (self < that)) == 0:
    return ">>>Llaves IGUALES<<<"
  else:
    return ">>>Llaves DIFERENTES<<<"

Tabla de tiempos

Tomando en cuenta que la ejecución se realizó en replit con una máquina de baja caracteristicas, se puede observar que a medida que se incrementa la dificultad en la generación del número primo p en base a los bits, el tiempo de ejecución aumenta exponencialmente.

Bits	Segundos
1024	6.89503
1128	8.88642
1232	9.90423
1336	10.9786
1440	12.613
1544	14.4639
1648	16.1857
1752	19.1532
1856	21.1139
1960	25.5909
2048	28.5619

luisballado/fund_ing_comp_labs