1.375-Approximation Algorithm for Sorting by Transpositions

This project implements an algorithm for sorting by transpositions with an approximation ratio of 1.375 for all permutations in the Symmetric Group. The algorithm and its details are presented in the paper "A new 1.375-approximation algorithm for Sorting By Transpositions" by L. A. G. Silva, L. A. B. Kowada, N. R. Rocco, and M. E. M. T. Walter.

Requirements

Maven version 3.6.3+
Java JDK 11+

Compilation

Before running any commands, compile the project with:

mvn compile

Running the Algorithm

To execute the proposed algorithm, use the command:

mvn exec:java -Dexec.mainClass="br.unb.cic.tdp.Silvaetal" -Dexec.args="<first_arg>"

Replace <first_arg> with the permutation to be sorted, for example:

mvn exec:java -Dexec.mainClass="br.unb.cic.tdp.Silvaetal" -Dexec.args="20,10,14,1,7,9,5,3,17,6,15,19,13,16,12,4,11,8,2,18"

Note that a large dataset, generated from a comprehensive case analysis, must be loaded into memory before executing the algorithm. This requires about 2GB of memory and takes approximately 15 seconds to complete on a computer with an 11th Gen Intel Core i9-11950H processor, 32GB DDR4 RAM, and a NVMe SSD. Ensure your computer has sufficient memory available.

Running the Case Analysis

To generate the case analysis, which forms the basis of the algorithm's correctness proof, use:

mvn exec:java -Dexec.mainClass="br.unb.cic.tdp.proof.ProofGenerator" -Dexec.args="<output_directory>"

Replace <output_directory> with the desired directory for the proof output. This process will utilize all CPU cores and can take hours or even days, depending on the CPU power.

The generated case analysis is available here.

What is "Sorting by Transpositions"?

A transposition consists in cutting a block of symbols from a permutation and pasting it elsewhere within the same permutation, or equivalently, swapping two adjacent blocks of symbols. The challenge is to determine the minimum number of transpositions required to sort a given permutation. This problem is NP-hard, as proven here.

The presented algorithm sorts any permutation using at most 1.375 times the known lower bound for the minimum number of transpositions needed.

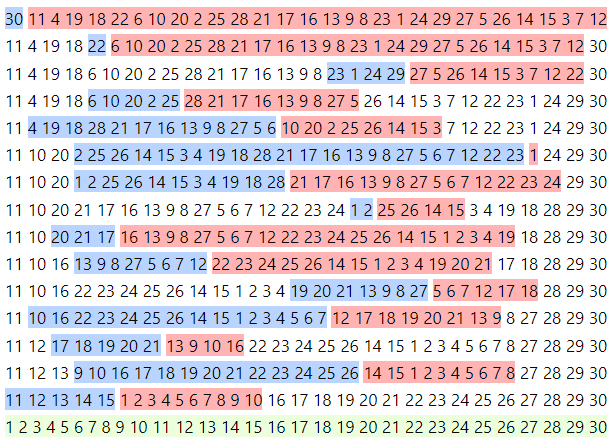
For example, the permutation 30,11,4,19,18,22,6,10,20,2,25,28,21,17,16,13,9,8,23,1,24,29,27,5,26,14,15,3,7,12 is sorted using 15 transpositions:

Additional Resources

Longer random permutations are available here (ignore the leading zeros).