TinySpline

TinySpline is a small, yet powerful library for interpolating, transforming, and querying arbitrary NURBS, B-Splines, and Bézier curves. The core of the library is written in ANSI C (C89) with a C++ wrapper for an object-oriented programming model. Based on the C++ wrapper, auto-generated bindings for C#, D, Go, Java, Javascript, Lua, Octave, PHP, Python, R, and Ruby are provided.

License

MIT License - see the LICENSE file in the source distribution.

Features

Object-oriented programming model
B-Splines of any degree and dimensionality
Spline interpolation
- Cubic natural
- Centripetal Catmull–Rom
Evaluation
- Knots
- Sampling (multiple knots at once)
- Components (find y for given x)
Knot insertion (refinement)
Bézier curve decomposition
Derivative
Degree elevation
Computation of rotation minimizing frames
Morphing
Serialization (JSON)
Vector math

Installation

Pre-built Binaries

Releases can be downloaded from the releases page. In addition, the following package manager are supported:

Conan (C/C++):
https://conan.io/center/tinyspline

NuGet (C#):

<PackageReference Include="tinyspline" version="0.4.0.1" />

Go:

go get github.com/tinyspline/go@v0.4.0

Luarocks (Lua):

luarocks install --server=https://tinyspline.github.io/lua tinyspline

Maven (Java):

<dependency>
   <groupId>org.tinyspline</groupId>
   <artifactId>tinyspline</artifactId>
   <version>0.4.0-1</version>
</dependency>

PyPI (Python):

python -m pip install tinyspline

On macOS, you may need to change the path to Python in _tinysplinepython.so via install_name_tool.

Compiling From Source

See BUILD.md.

Getting Started

A variety of examples (unit tests) can be found in the test subdirectory. The examples subdirectory contains at least one example for each interface (target language).

The following listing shows a python example:

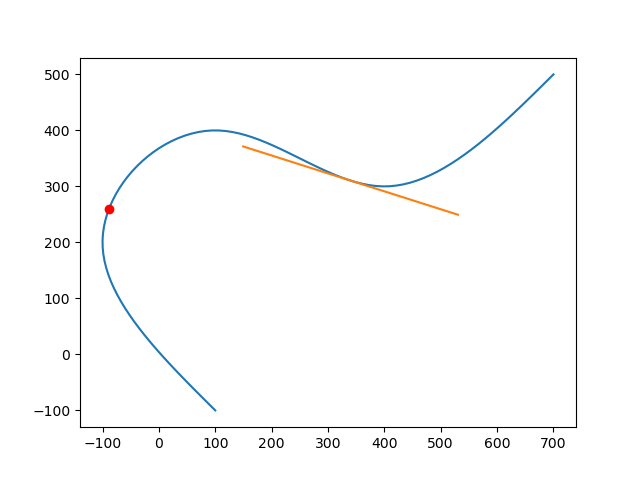
from tinyspline import *
import matplotlib.pyplot as plt

spline = BSpline.interpolate_cubic_natural(
  [
     100, -100, # P1
    -100,  200, # P2
     100,  400, # P3
     400,  300, # P4
     700,  500  # P5
  ], 2) # <- dimensionality of the points

# Draw spline as polyline.
points = spline.sample(100)
x = points[0::2]
y = points[1::2]
plt.plot(x, y)

# Draw point at knot 0.3.
vec2 = spline.eval(0.3).result_vec2()
plt.plot(vec2.x, vec2.y, 'ro')

# Draw tangent at knot 0.7.
pos = spline(0.7).result_vec2() # operator () -> eval
der = spline.derive()(0.7).result_vec2().norm() * 200
s = (pos - der)
t = (pos + der)
plt.plot([s.x, t.x], [s.y, t.y])

plt.show()

The resulting image:

Theoretical Backgrounds

[1] is a very good starting point for B-Splines.

[2] explains De Boor's Algorithm and gives some pseudo code.

[3] provides a good overview of NURBS with some mathematical background.

[4] is useful if you want to use NURBS in TinySpline.

lxyo/tinyspline