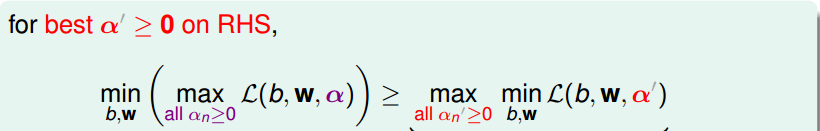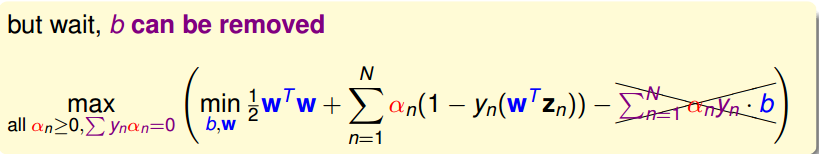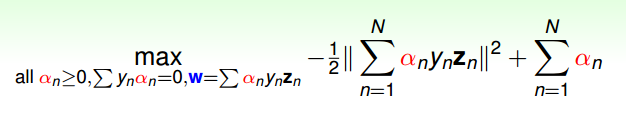对偶支持向量机
咦?怎么还有关于支持向量机的内容,我们不是在上一讲已经将支持向量机解决了么?怎么又引入了对偶这个概念?
1.动机
我们在上一讲已经讲过,可以使用二次规划来解决支持向量机的问题。如果现在想要解决非线性的支持向量机的问题,也很简单,如下图所示:
我们只需要将原来的有关于X的内容通过转换变为Z,剩下的事情就一样了。在Z空间里面,将Q,P,A,C等填充好,然后丢到一个二次规划的软件里去求得一个Z空间的最佳的w和b。所以我们需要解决的是Z空间的二次规划问题,我们想象一下,但是当我们Z空间的维度(d)很高时(甚至无限维),我们的二次规划解起来具有一定的挑战性。
所以说,如果我们想要做高维度特征的SVM,如何移除掉对于特征维度的依赖?使高维甚至无限维的特征的SVM称为可能?这就是我们考虑对偶支持向量机的动机。
2. 学习的对偶算法
因为我们的SVM的原始问题是一个受限制的最优化问题,回想之前做regularization时候,我们的regularization也是一个受限制的最优化问题,我们应用拉格朗日乘数法,来得到一个不受限制的正则项表达式。同理,我们也可以在此应用拉格朗日乘数法,将有条件的SVM问题变成没有条件的SVM问题,紧接着利用拉格朗日对偶性,得到对偶问题,对偶中可以有效地移除对特征维度的依赖性,所以我们可以用过求解对偶问题来得到原始问题的最优解。如果对拉格朗日乘数法不理解,可以点击如下链接:拉格朗日乘数法,这个视频讲得很不错的。
2.1 拉格朗日函数
首先构建拉格朗日函数:
我们的拉格朗日函数由两部分组成
- 第一部分:原始的目标函数
- 第二部分:对原始问题的每一个限制条件均乘上一个朗格朗日乘子,然后在求和
现在拉格朗日函数写出来了,那如何来求解拉格朗日函数来求得我们的最优解呢?(也就是说函数写出来了,你是通过最大值还是最小值来求最佳解?)
2.1.1 拉格朗日原始问题
通过拉格朗日函数,我们可以求解的SVM问题写为如下形式。解释一下下面这个形式所表达的意义
- 首先选定一个(w,b)
- 然后找到a使L()的值最大
- 然后通过w,b,a计算L()的值
- 选定另一个(w,b)做相同的步骤,得出相应的L()值
- 选定完所有的(w,b)之后,找出L()值最小的wb,即是最优解
为什么可以写成这个形式呢?这个问题的最优解和原始问题一致么?下面我们就来证明这件事情。
算法的第一步是选出一个(w,b)来,选出的这个(w, b)有两种可能:
- 如果选出来的(w, b)是坏的,也就是说我们的(w, b)会违反某些限制条件,也就是说某些1-Yn(W.Zn + b)的项本来是要小于等于0的,现在大于0了,那如果对an(1-Yn(W.Zn + b))求最大值,那最终L()就是无穷大了。
- 如果选出来的(w, b)是好的,也就是说(w, b)满足所有的限制条件,也就是所有的1-Yn(W.Zn + b)要小于等于0,那an(1-Yn(W.Zn + b))什么时候能够得到最大值呢?那就是an等于0才是最大值。当an等于0时,我们的问题就剩下min 1/2 w * w了(原始的最优化问题)。
根据之前所说表达式的意义,最后一步是选出L()值最小的(w, b),由于那些坏的(w, b)的L()值为无穷大,所以那些坏的(w, b)被自动排除了。剩下的就是从好的(w, b)(他们的an均为0)中,选出使L()=1/2 w * w的值最小的(w, b)。所以这不就是我们原始问题做的事情么?
所以朗格朗日函数的最优解也就是我们原始问题的最优解。
2.1.2 拉格朗日对偶问题
接下来我们继续对拉格朗日函数做变换,来实现我们‘动机’章节所说的消除对特征维度的依赖。
如下图所示,可以很容易得出下图的结论
图中大于号右侧的表达式表示仅仅根据b.w来求表达式的最小值,a为一个任意的固定值。大于号左侧的表达式表示先求表达式关于a的最大值,然后再求关于b.w的最小值,所以显而易见不等式成立。也就是说,对于右侧的任何一个固定的a值,都有以上结果。
进一步地,既然任意的a都有以上结果,那现在在右侧加一个max的动作的话,那不等式也依然成立咯。
上图中不等式右侧的式子又叫做拉格朗日原始问题(注意这里指的是拉格朗日原始问题,并不是SVM的原始问题,不要混淆)的对偶问题,可以看出对偶问题将原始问题的max/min对调了。
但是从图中我们可以看出,原始问题和对偶问题是大于等于的关系,那么拉格朗日对偶问题的最优解也是拉格朗日原始问题的最优解么?
在最佳化文献中,我们管 >= 叫做weak duality,弱的对偶关系。但是我们不想要这种关系,我们能不能够直接将上式从不等式变为等式呢?变为等式后,对偶问题的最佳解就是原始问题的最佳解了。
那么有没有什么理论来保证这个等式成立呢?做在最佳化理论中,如果我们的SVM原始问题(QP问题)满足以下条件:
- 目标函数是凸的
- 是有解的(也就是能找到一条线将资料正确分开)
- 线性的限制条件(QP本来就有)
那我们的强对偶关系就成立。所以就可以通过解对偶问题来得到原始问题的最优解。我们把对偶问题的推导过程叫做拉格朗日对偶性
2.2 求解拉格朗日对偶问题
现在的拉格朗日对偶问题的形式如下:
我们可以看到,在大括号内部,是一个关于wb的无条件的最优化问题。请记住我们的初衷,我们是想移除掉特征维度的依赖,所以我们接下来的事情就是通过某些关系来将w,b从我们的问题中移除。
2.2.1 KKT condition
对于我们的对偶问题,大括号内部是关于w和b的无条件最优化问题。无条件最优化问题我们会解啊,可以分别对w和b求偏微分等于0,就可以分别得到w和b的表达式。好,现在就来做
首先来对b做偏微分:
上式的结果不必多说吧,我们再把上式的结果带回函数中,会发现b被成功地消除掉了:
然后我们在对w做偏微分:
可以将w用另一个表达式表示出来,所以可以将该表达式带回原函数中,将w用anynzn来表示:
经过上面的步骤,w和b已经基本消失了,对偶问题中的min也不用做了,剩下的事情就是做关于a的最优化(有条件限制的最优化)。
上图中表示的就是我们导出来的简化版的拉格朗日对偶问题。
从我们的推导过程可知,我们的最佳的a,w,b会满足某些关系,我们把这些关系叫做KKT condition:
下面我们来一一解释KKT条件:
- 第一条是我们原始的SVM问题要满足的条件
- 第二条使我们拉格朗日原始/对偶问题的条件
- 第三条是我们对拉格朗日对偶问题的w,b参数做偏微分所得出的结论
- 第四条,我们在2.1.1节中,将SVM的原始问题(受限制)转换为拉格朗日原始问题(不受限)的过程中,证明该转换的有效性时,得出的一个结论。
这些条件有什么用呢?待会儿可以看到,当我们求出a后,可以用这些条件来求w和b。
2.2.2 求解对偶问题
上一小结中我们得到了简化版的拉格朗日对偶问题,现在我们来做一点儿小小的变动,使其变成我们习惯的形式。
w的表达式我们没有将其作为条件列出来,因为现在求解的是a的问题,和w的限制条件没有关系,所以没将其列出来。
我们的新的问题有N个变量和N+1个条件,而且新问题还是一个凸的二次规划问题(目标函数为二次,限制条件为一次),所以说我们大费周章地将一个QP问题转换为另一个QP问题,这是因为点啥呢?哈哈,就是为了消除掉对特征维度的依赖啊,还有一个目的是为了引出很好用的kernel方法(请看下一篇文章)。
好,既然是新的QP问题,那解法当然和就的QP问题差不多啦,将所有的系数算出来,然后丢给二次规划软件就搞定啦。所以解法就不啰嗦了,看下图:
这里有一点值得注意,我们的条件式里面有一个是等于符号的条件(虽然MATLAB里面有处理等于条件的,但是MATLAB要求等于的条件的系数是矩阵,而我们只有y向量,所以不适用),而我们的QPsolver软件一般要求的是不等式条件,所以我们就把等式条件∑ynan=0可以转变为两个条件不等式条件:
- ∑ynan >= 0
- ∑ynan <= 0
所以写成向量的形式就是:
- y.a >= 0向量
- -y.a >= -0向量
然后把上述两个不等式和问题中本来有的不等式结合,就得出了不等式的系数矩阵A
- [
- [y..]
- [-y..]
- [ I..]
- .
- .
- ]
这是一个(N+2)x(N)大小的矩阵,其中第一行第二行分别为y和-y向量,剩余的就是一个NxN的单位矩阵。对应地,C向量是一个N+2 x 1的向量
2.2.3 警告
在我们解决QP问题的过程中,会有一个二次系数矩阵Q,这个矩阵的大小是N x N的,从上一小节我们知道,Qmn = ym.yn.Zm.Zn, 当Zm与Zn垂直时,Qmn为0,但是Z向量垂直的情况毕竟是少数,也就是说我们的Q矩阵的元素大多数都不是0,我们管Q叫做密集的。
现在我们来看看,当N = 30000时(有30000个样本),就算Q是对称矩阵,只存一半,也需要花 > 3G 的内存来存储这些系数,所以这个Q矩阵很大。所看看起来没有原始的SVM的二次规划问题那么好解,原始SVM的QP问题的Q矩阵比较特殊,里面包含一个单位矩阵,只有对角线才有值,所以会占用比较少的内存。
所以我们通常在解决SVM问题的时候,不会使用一个通用的QP软件,而是会使用特殊的专为SVM设计的二次规划软件。也就是这种软件不会要求将Q矩阵先算出来,而是用到的时候再去算。
2.2.4 求解b,w
假设我们通过二次规划软件将a解出来了,那么现在怎么得出b,w呢?
我们之前说过,KKT condition可以帮我们求解w和b。
- 求解w : 求解w就很简单了,直接使用KKT条件的第三项
- 求解b : 求解b也不难,利用KKT条件的最后一项。我们知道,当an不等于0时,1-yn(wzn + b)肯定等于0。现在我们知道了所有的a,所以就找一个an不等于0的点,将其代入,求得b即可。
2.2.5 a的稀疏性
根据KKT条件,我们可以轻易得出,a的解具有稀疏性(向量内的大多元素为0)。当yn(wzn+b)不等于1时,也就是该点位于我们的边界外时,这是我们的这些数据点的大多数的分布,根据KKT条件中的complementary slackness条件,我们得知,an为0,也就是大多数数据点的an为0,这也就说明了an的稀疏性。
3. 对偶算法的总结
从解w和b的过程中,我们知道。当an > 0时,1-yn(wzn + b)肯定等于0(KKT条件最后一项),也就是说yn(wzn + b) = 1,也就是说该(zn,yn)点的函数间隔等于1,所以说,该点处于边界上。也就是说所有an>0的点均位于边界上,对我们的边界起到一个支撑作用。我们这些位于边界上的点叫做支撑向量。其他非支撑向量的点,也就是an = 0的点对我们的边界的构建没有贡献,从w和b的表达式可以看出,an等于0的点不会贡献任何力量。
(注意:an > 0的点一定位于边界上,但是位于边界上的点并不一定是an > 0的。所以我们仅仅把an > 0的点叫做支撑向量)
所以,我们计算w和b的时候仅仅需要支撑向量的点就行了
3.1 两种形式的hard-margin SVM
到现在我们已经学习两种形式的hard-margin SVM(hard-margin表示保证资料不违反边界),分别是原始的SVM问题和对偶的SVM问题:
我们从原始问题的d空间切换到了新问题的N空间,原始问题比较适合解决d较小的情况,对偶问题适合解决N较小的情况
两个问题解决完成之后,都可以得到一个最佳的w,b,通过这个w,b就能得到我们的hypothesis: