/NMFLibrary

MATLAB library for non-negative matrix factorization (NMF): Version 1.8.0

Primary LanguageMATLABMIT LicenseMIT

NMFLibrary

Matlab library for non-negative matrix factorization (NMF)

Authors: Hiroyuki Kasai

Last page update: May 21, 2019

Latest library version: 1.8.0 (see Release notes for more info)


Introduction

The NMFLibrary is a pure-Matlab library of a collection of algorithms of non-negative matrix factorization (NMF).


List of the algorithms available in NMFLibrary


Algorithm configurations

Category Name in example codes function options.alg other options
Base MU-EUC nmf_mu mu metric='EUC'
MU-KL nmf_mu mu metric='KL'
MU-ALPHA nmf_mu mu metric='ALPHA-D'
MU-BETA nmf_mu mu metric='BETA-D'
Modified MU nmf_mu mod_mu
Acceralated MU nmf_mu acc_mu
PGD nmf_pgd pgd
Direct PGD nmf_pgd direct_pgd
ALS nmf_als als
Hierarchical ALS nmf_als hals_mu
Acceralated hierarchical ALS nmf_als acc_hals_mu
ASGROUP nmf_anls anls_asgroup
ASGIVENS nmf_anls anls_asgivens
BPP nmf_anls anls_bpp
Variant Semi-NMF semi_nmf
NeNMF nenmf
GNMF GNMF
SDNMF SDNMF
Sparse sparseMU-EUC nmf_sparse_mu metric='EUC'
sparseMU-KL nmf_sparse_mu metric='KL'
sparseNMF sparse_nmf
NMFsc nmf_sc
nsNMF ns_nmf
fnsNMF ns_nmf metric='EUC', update_alg='apg'
Orthogonal DTPP nmf_dtpp
orthMU nmf_orth_mu
OrthNMF
NMF-HALS-SO
Symmetric SymmANLS symm_anls
SymmHALS symm_halsacc
SymmNewton symm_newton
Online INMF inmf
ONMF onmf
Acceralated ONMF omf_acc
SPG spg_nmf
RONMF ronmf
SAGA-MU-NMF asag_mu_nmf
SMU smu_nmf
SVRMU svrmu_nmf
Probabilistic PNMF-VB pnmf_vb
PNMF-GIBBS pnmf_gibbs

Folders and files

./                      - Top directory.
./README.md             - This readme file.
./run_me_first.m        - The scipt that you need to run first.
./demo.m                - Demonstration script to check and understand this package easily. 
./demo_face.m           - Demonstration script to check and understand this package easily. 
|plotter/               - Contains plotting tools to show convergence results and various plots.
|auxiliary/             - Some auxiliary tools for this project.
|solver/                - Contains various optimization algorithms.
    |--- base/          - Basic NMF solvers.
    |--- online/        - Online/stochstic NMF solvers.
    |--- sparse/        - Sparse NMF solvers.
    |--- robust/        - Robust NMF solvers.
    |--- orthogonal/    - Orthogonal NMF solvers.
    |--- symm/          - Symmetric NMF solvers.
    |--- nenmf/         - Nesterov's accelerated NMF solver.
    |--- probabilistic/ - Probabilistic NMF solvers.
    |--- 3rd_party/     - Solvers provided by 3rd_party.

First to do

Run run_me_first for path configurations.

%% First run the setup script
run_me_first;

Simplest usage example: 4 steps!

Just execute demo for the simplest demonstration of this package. .

%% Execute the demonstration script
demo;

The "demo.m" file contains below.

%% generate synthetic data non-negative matrix V size of (mxn)
m = 500;
n = 100;
V = rand(m,n);
    
%% Initialize rank to be factorized
rank = 5;

%% perform factroization
% MU
options.alg = 'mu';
[w_nmf_mu, infos_nmf_mu] = nmf_mu(V, rank, options);
% Hierarchical ALS
options.alg = 'hals';
[w_nmf_hals, infos_nmf_hals] = nmf_als(V, rank, options);        
    
%% plot
display_graph('epoch','cost', {'MU', 'HALS'}, {w_nmf_mu, w_nmf_hals}, {infos_nmf_mu, infos_nmf_hals});

Let's take a closer look at the code above bit by bit. The procedure has only 4 steps!

Step 1: Generate data

First, we generate synthetic data of V of size (mxn).

m = 500;
n = 100;
V = rand(m,n);

Step 2: Define rank

We set the rank value.

rank = 5;

Step 3: Perform solver

Now, you can perform optimization solvers, e.g., MU and Hierarchical ALS (HALS), calling solver functions, i.e., nmf_mu() function and nmf_als() function after setting some optimization options.

% MU
options.alg = 'mu';
[w_nmf_mu, infos_nmf_mu] = nmf_mu(V, rank, options);
% Hierarchical ALS
options.alg = 'hals';
[w_nmf_hals, infos_nmf_hals] = nmf_als(V, rank, options);

They return the final solutions of w and the statistics information that include the histories of epoch numbers, cost values, norms of gradient, the number of gradient evaluations and so on.

Step 4: Show result

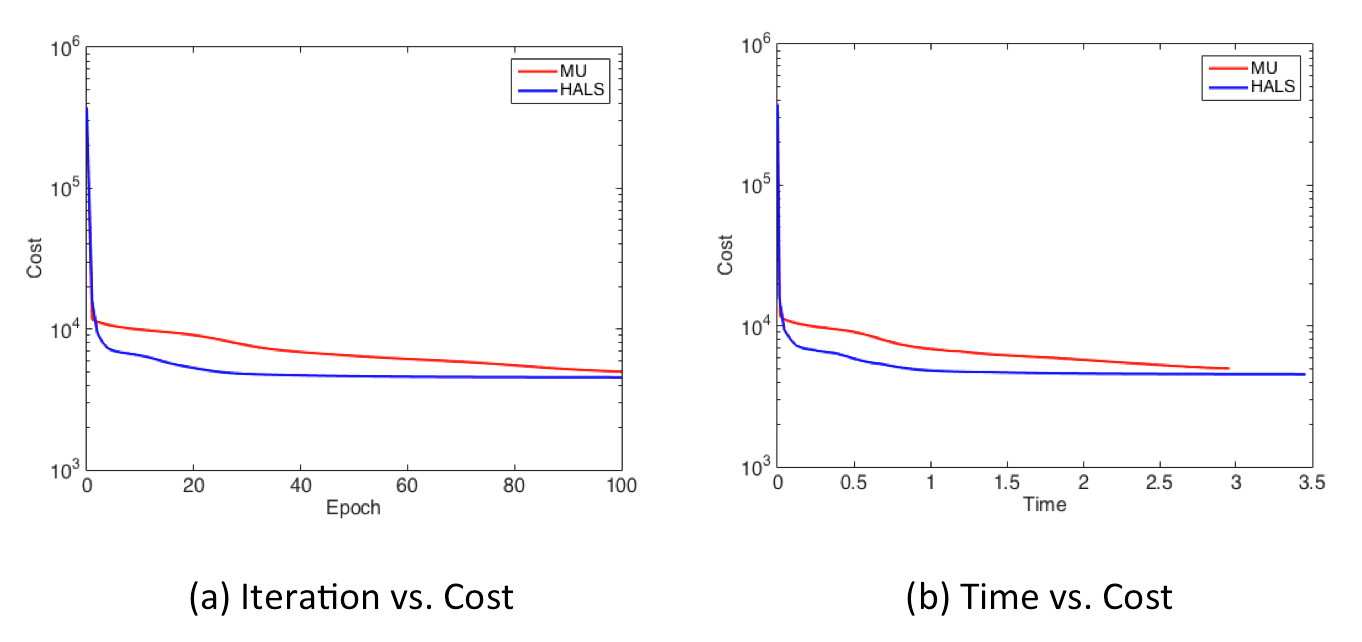
Finally, display_graph() provides output results of decreasing behavior of the cost values in terms of the number of iterrations (epochs) and time [sec].

display_graph('epoch','cost', {'MU', 'HALS'}, {w_nmf_mu, w_nmf_hals}, {infos_nmf_mu, infos_nmf_hals});
display_graph('time','cost', {'MU', 'HALS'}, {w_nmf_mu, w_nmf_hals}, {infos_nmf_mu, infos_nmf_hals});

That's it!


More plots

"demo_face.m" illustrates the learned basis (dictrionary) in case of CBCL face datasets.

The dataset is first loaded into V instead of generating synthetic data in Step 1.

V = importdata('./data/CBCL_face.mat');

Then, we can display basis elements (W: dictionary) obtained with different algorithms additionally in Step 4.

plot_dictionnary(w_nmf_mu.W, [], [7 7]); 
plot_dictionnary(w_nmf_hals.W, [], [7 7]);


License

  • The NMFLibrary is free, non-commercial and open source.
  • The code provided iin NMFLibrary should only be used for academic/research purposes.
  • Third party files are included.
    • For ANLS algorithms: nnlsm_activeset.m, nnls1_asgivens.m, nnlsm_blockpivot.m, and normalEqComb.m written by Jingu Kim.
    • For PGD algorithm: nlssubprob.m.
    • For GNMF algorithm: GNMF.m, GNMF_Multi.m, constructW.m and litekmeans.m writtnen by Deng Cai.
    • For SDNMF algorithm: SDNMF.m, and SDNMF_Multi.m writtnen by Wei Qian.
    • For symmetric algorithms writtnen by D.Kang et al. and Z. Zhu et al.
    • For acceleration sub-routines in nmf_mu.m and nmf_als.m for MU and HALS from Nicolas Gillis.
    • For dictionaly visualization: plot_dictionnary.m, rescale.m, and getoptions.m.

Problems or questions

If you have any problems or questions, please contact the author: Hiroyuki Kasai (email: kasai at is dot uec dot ac dot jp)


Release notes

  • Version 1.7.0 (June 27, 2019)
    • Symmetic solvers are added.
    • Clustering quality measurements are integrated into store_nmf_infos.m.
  • Version 1.7.0 (May 21, 2019)
    • PNMF-VB and NeNMF are added.
    • Fixed some bugs.
  • Version 1.6.0 (May 16, 2019)
    • DTPP is added.
  • Version 1.5.1 (Apr. 22, 2019)
    • Some solvers are modified to fix bugs.
  • Version 1.5.0 (Jul. 30, 2018)
    • fnsNMF and NMF-HALS-SO are added.
  • Version 1.4.0 (Jul. 24, 2018)
    • sparseMU and orthMU are added.
    • MU with Kullback-Leibler divergence (KL), Amari alpha divergence, and beta divergenceare added.
  • Version 1.3.0 (Jul. 23, 2018)
    • NMFsc, scNMF and csNMF are added.
  • Version 1.2.0 (Jul. 21, 2018)
    • GNMF, Semi-NMF and SDNMF are added.
  • Version 1.1.0 (Apr. 17, 2018)
    • Online/stochastic solvers are added.
  • Version 1.0.0 (Apr. 04, 2017)
    • Initial version.