Anticlustering partitions a pool of elements into clusters (or
anticlusters) with the goal of achieving high between-cluster
similarity and high within-cluster heterogeneity. This is accomplished
by maximizing instead of minimizing a clustering objective function,
such as the intra-cluster variance (used in k-means clustering) or the
sum of pairwise distances within clusters. The package anticlust
implements anticlustering methods as described in Papenberg and Klau
(2021;
https://doi.org/10.1037/met0000301),
Brusco et al. (2020;
https://doi.org/10.1111/bmsp.12186),
and Papenberg (2024;
https://doi.org/10.1111/bmsp.12315).
The stable release of anticlust is available from
CRAN and can be
installed via:
install.packages("anticlust")
A (potentially more recent) version of anticlust can also be installed
via R Universe:
install.packages('anticlust', repos = c('https://m-py.r-universe.dev', 'https://cloud.r-project.org'))
or directly via Github:
library("remotes") # if not available: install.packages("remotes")
install_github("m-Py/anticlust")
If you use anticlust in your research, it would be courteous if you
cite the following reference:
- Papenberg, M., & Klau, G. W. (2021). Using anticlustering to partition data sets into equivalent parts. Psychological Methods, 26(2), 161–174. https://doi.org/10.1037/met0000301
Depending on which anticlust functions you are using, including other
references may also be fair. Here you can find out in detail how to
cite anticlust.
Another great way of showing your appreciation of anticlust is to
leave a star on this Github repository.
This README contains some basic information on the R package
anticlust. More information is available via the following sources:
- A paper is available describing the theoretical background of
anticlustering and the
anticlustpackage in detail (https://doi.org/10.1037/met0000301). The freely available preprint can be retrieved from https://psyarxiv.com/3razc/. A more recent paper focusing on the k-plus anticlustering method can be retrieved from https://psyarxiv.com/7jw6v/. - The
Rdocumentation of the main functions is actually quite rich and up to date, so you should definitely check that out when using theanticlustpackage (primarily?anticlustering,?kplus_anticlustering,?balanced_clustering, and?matching). - A video is available in German
language where I illustrate the main functionalities of the
anticlustering()function. My plan is to make a similar video in English in the future. - The package website contains all documentation as a convenient website. At the current time, the website also lists four package vignettes, while additional vignettes are planned.
In this initial example, I use the main function anticlustering() to
create five similar sets of plants using the classical iris data set:
First, load the package via
library("anticlust")
Call the anticlustering() method:
anticlusters <- anticlustering(
iris[, -5],
K = 5,
objective = "kplus",
method = "local-maximum",
repetitions = 10
)
The output is a vector that assigns a group (i.e, a number between 1 and
K) to each input element:
anticlusters
#> [1] 1 2 4 5 3 4 2 3 2 2 1 5 1 2 4 1 2 3 2 5 1 5 4 5 1 1 3 4 5 5 5 4 5 2 1 1 3
#> [38] 4 3 3 4 2 3 5 2 5 3 4 3 1 2 2 5 1 2 3 3 4 4 1 5 1 2 3 3 1 2 4 4 4 4 1 3 4
#> [75] 2 4 5 2 5 2 3 3 1 5 4 1 5 3 2 1 2 5 3 4 1 4 1 2 4 5 2 2 3 1 4 1 3 4 4 5 3
#> [112] 2 3 1 5 2 5 3 1 5 4 1 2 5 1 2 3 1 3 3 5 1 2 5 5 4 3 5 4 3 5 5 1 4 4 1 3 4
#> [149] 2 2
By default, each group has the same number of elements (but the argument
K can be adjusted to request different group sizes):
table(anticlusters)
#> anticlusters
#> 1 2 3 4 5
#> 30 30 30 30 30
Last, let’s compare the features’ means and standard deviations across groups to find out if the five groups are similar to each other:
knitr::kable(mean_sd_tab(iris[, -5], anticlusters), row.names = TRUE)
| Sepal.Length | Sepal.Width | Petal.Length | Petal.Width | |
|---|---|---|---|---|
| 1 | 5.84 (0.84) | 3.06 (0.44) | 3.76 (1.79) | 1.20 (0.77) |
| 2 | 5.84 (0.84) | 3.06 (0.45) | 3.76 (1.79) | 1.20 (0.77) |
| 3 | 5.84 (0.84) | 3.06 (0.44) | 3.75 (1.79) | 1.20 (0.77) |
| 4 | 5.85 (0.84) | 3.05 (0.45) | 3.76 (1.79) | 1.21 (0.77) |
| 5 | 5.84 (0.84) | 3.06 (0.44) | 3.76 (1.79) | 1.19 (0.78) |
As illustrated in the example, we can use the function
anticlustering() to create similar groups of plants. In this case
“similar” primarily means that the means and standard deviations (in
parentheses) of the variables are pretty much the same across the five
groups. The function anticlustering() takes as input a data table
describing the elements that should be assigned to sets. In the data
table, each row represents an element (here a plant, but it can be
anything; for example a person, word, or a photo). Each column is a
numeric variable describing one of the elements’ features. The number of
groups is specified through the argument K. The argument objective
specifies how between-group similarity is quantified; the argument
method specifies the algorithm by which this measure is optimized. See
the documentation ?anticlustering for more details.
Five anticlustering objectives are natively supported in
anticlustering():
- the “diversity” objective, setting
objective = "diversity"(default) - the “average-diversity”, setting
objective = "average-diversity", which normalizes the diversity by cluster size - the k-means objective (i.e., the “variance”) setting
objective = "variance" - the “k-plus” objective, an extension of the k-means variance
criterion, setting
objective = "kplus" - the “dispersion” objective (the minimum distance between any two
elements within the same cluster), setting
objective = "dispersion"
The anticlustering objectives are described in detail in the
documentation (?anticlustering, ?diversity_objective,
?variance_objective, ?kplus_anticlustering, ?dispersion_objective)
and the references therein. It is also possible to optimize user-defined
objectives, which is also described in the documentation
(?anticlustering).
Sometimes, it is required that sets are not only similar with regard to
some numeric variables, but we also want to ensure that each set
contains an equal number of elements of a certain category. Coming back
to the initial iris data set, we may want to require that each set has a
balanced number of plants of the three iris species. To this end, we can
use the argument categories as follows:
anticlusters <- anticlustering(
iris[, -5],
K = 3,
categories = iris$Species
)
## The species are as balanced as possible across anticlusters:
table(anticlusters, iris$Species)
#>
#> anticlusters setosa versicolor virginica
#> 1 17 17 16
#> 2 17 16 17
#> 3 16 17 17
Anticlustering creates sets of dissimilar elements; the heterogenity
within anticlusters is maximized. This is the opposite of clustering
problems that strive for high within-cluster similarity and good
separation between clusters. The anticlust package also provides
functions for “classical” clustering applications:
balanced_clustering() creates sets of elements that are similar while
ensuring that clusters are of equal size. This is an example:
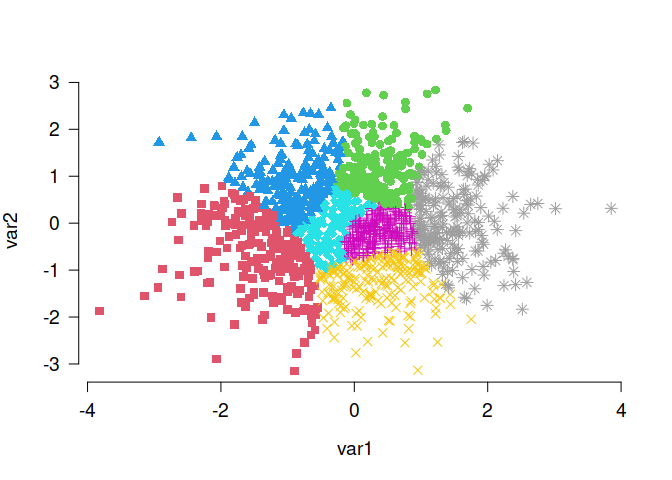
# Generate random data, cluster the data set and visualize results
N <- 1400
lds <- data.frame(var1 = rnorm(N), var2 = rnorm(N))
cl <- balanced_clustering(lds, K = 7)
plot_clusters(lds, clusters = cl, show_axes = TRUE)
The function matching() is very similar, but is usually used to find
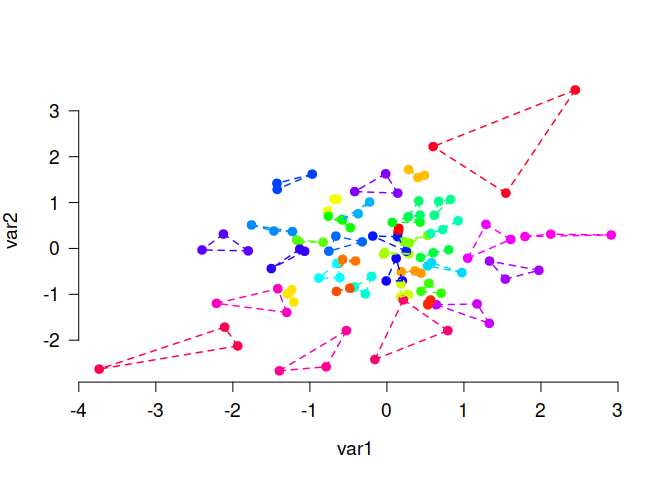
small groups of similar elements, e.g., triplets as in this example:
# Generate random data and find triplets of similar elements:
N <- 120
lds <- data.frame(var1 = rnorm(N), var2 = rnorm(N))
triplets <- matching(lds, p = 3)
plot_clusters(
lds,
clusters = triplets,
within_connection = TRUE,
show_axes = TRUE
)
If you have any question on the anticlust package or find some bugs, I
encourage you to open an issue on the Github
repository.