This tiny package determines a set of Pareto optimal vectors, also known as maximal vectors, from a larger set of vectors. In database area, this is also known as the "skyline operator".
Each vector is n dimensional and for each dimension we can choose
the optimality to be either min or max. This is governed by two
vectors min_idxs and max_idxs. For an indice in min_idxs the
optimal value is considered to be a min and analogously for max_idxs.
Note that there is no error checking on the arrays min_idxs and
max_idxs. So an index cannot be in both min_idxs and max_idxs
and all indices in both must be legal indices of the input vector.
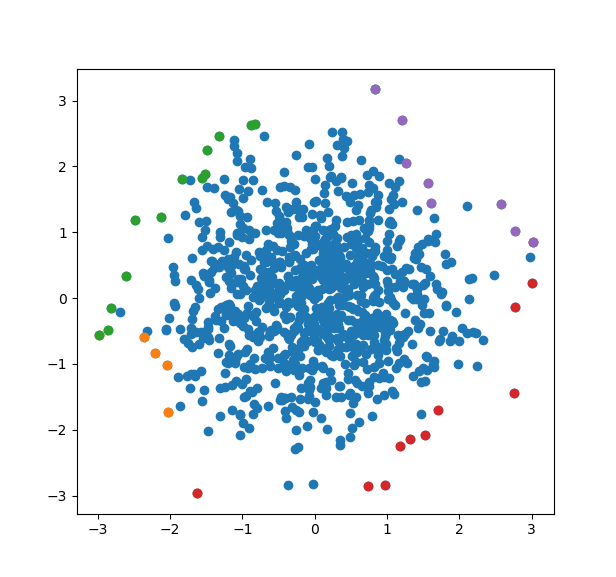
Here is an example of calculating all 4 different Pareto frontiers in two dimensions.
using ParetoFront
using PyPlot
pareto = [Set{Vector{Float64}}() for _ in 1:4]
mins = [[1,2], [1], [2], []]
maxs = [ [], [2], [1], [1,2]]
v = randn(1000, 2)
for x in eachrow(v)
for i in 1:4
update_pareto!(pareto[i], x, mins[i], maxs[i])
end
end
scatter(v[:,1], v[:,2])
for i in 1:4
front = Matrix(reduce(hcat, collect(pareto[i]))')
scatter(front[:,1], front[:,2])
end
And we can see the four different Pareto frontiers here
Finally we note that this is fairly simple and direct algorithm. The algorithm in [1], on the other hand, is fairly complex. It uses multipass, sorting, windowing, merging and multi-threading. On a test of 500,000 records in 7 dimensions, where all the values are between 1 and 10,000, it extracts the maximal vectors in about 15 seconds on a 733 MHz Pentium III machine. Using ParetoFront on a Intel® Core™ i9-9980HK CPU, single threaded, it can extract the maximal vectors in 33 seconds. Of course this is cheating in at least two ways, both due to Moore's law. The obvious one is that the processors are so much faster. The second is that with 64GB of memory, the entire data set fits in main memory and no IO is needed.