Most students are quite familiar with functional-level (FL) and register-transfer-level (RTL) modeling from ECE 4750, but students are often less familiar with cycle-level (CL) modeling. Here is a reminder of the differences between these modeling levels:
-
Functional-Level: FL models implement the functionality but not the timing of the hardware target. FL models are useful for exploring algorithms, performing fast emulation of hardware targets, and creating golden models for verification of CL and RTL models. FL models can also be used for building sophisticated test harnesses. FL models are usually the easiest to construct, but also the least accurate with respect to the target hardware.
-
Cycle-Level: CL models capture the cycle-approximate behavior of a hardware target. CL models will often augment the functional behavior with an additional timing model to track the performance of the hardware target in cycles. CL models are usually specifically designed to enable rapid design-space exploration of cycle-level performance across a range of microarchitectural design parameters. CL models attempt to strike a balance between accuracy, performance, and flexibility.
-
Register-Transfer-Level: RTL models are cycle-accurate, resource-accurate, and bit-accurate representations of hardware. RTL models are built for the purpose of verification and synthesis of specific hardware implementations. RTL models can be used to drive EDA toolflows for estimating area, energy, and timing. RTL models are usually the most tedious to construct, but also the most accurate with respect to the target hardware.
The tutorial on PyMTL introduced all three levels of modeling, but we will review the CL models for the sort unit and GCD unit here. We will also explore a new CL model for a simple cache, and we will discuss a sophisticated CL modeling framework used to model complex superscalar out-of-order processors. Please keep in mind that developing a CL model is required for lab 1 and may be required for lab 2. While CL modeling is not required for the project, students may find that CL modeling can facilitate a much broader initial design-space exploration, and thus enable students to focus on the most promising designs for RTL implementation.
The first step is to source the setup script, clone this repository from GitHub, and make a build directory to work in.
% source setup-ece5745.sh
% mkdir $HOME/ece5745
% cd $HOME/ece5745
% git clone git@github.com:cornell-ece5745/ece5745-sec-pymtl-cl
% mkdir -p ece5745-sec-pymtl-cl/pymtl/build
% cd ece5745-sec-pymtl-cl/pymtl/build
% BUILDDIR=$PWD
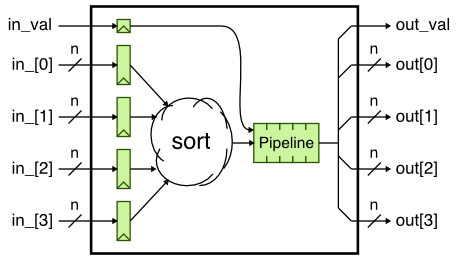
We will start by reviewing the sort unit CL model first introduced in the PyMTL tutorial and shown in the following figure. We immediately sort the input values in a single cycle, and then we delay sending the response by several cycles to model the pipeline latency. The key to CL modeling is to capture the cycle-level behavior (i.e., how long a transaction takes in cycles) without worrying about the bit-level details or the exact hardware structures required to implement the desired cycle-level behavior.
Here is the corresponding code for the sort unit CL model.
class SortUnitCL( Model ):
def __init__( s, nbits=8, nstages=3 ):
s.in_val = InPort (1)
s.in_ = [ InPort (nbits) for _ in range(4) ]
s.out_val = OutPort(1)
s.out = [ OutPort (nbits) for _ in range(4) ]
s.pipe = deque( [[0,0,0,0,0]]*(nstages-1) )
@s.tick_cl
def block():
s.pipe.append( deepcopy( [s.in_val] + sorted(s.in_) ) )
data = s.pipe.popleft()
s.out_val.next = data[0]
for i, v in enumerate( data[1:] ):
s.out[i].next = vWe can use any Python code we want to implement a CL model. Here we use
Python's built-in sorted function to do the actual sorting operation on
the input values. Notice how we use a deque to model the pipeline
behavior. Each entry in the deque has a valid bit and then the four
sorted values. Also notice how we need to use a deepcopy to ensure that
we really do have a copy of the sorted values in the deque and not just
a reference. This is very common CL modeling pattern: we do all of the
real work in the first cycle and then delay the response to model the
desired latency. Let's run the sort unit CL tests and then produce a line
trace:
% cd $BUILDDIR
% py.test ../tut3_pymtl/sort/SortUnitCL_test.py
% py.test ../tut3_pymtl/sort/SortUnitCL_test.py -k test[2stage_stream] -s
2: {04,03,02,01}|
3: {09,06,07,01}|
4: {04,08,00,09}|{01,02,03,04}
5: |{01,06,07,09}
6: |{00,04,08,09}
We can see that the first transaction goes into the sort unit on cycle 2 and then comes out of the sort unit on cycle 4. The sort unit CL model is modeling a two-stage pipeline. Since CL modeling is a higher level modeling abstraction compared to RTL modeling, it is much easier to experiment with different parameters. For example, we can easily experiment with longer latency sort units and analyze the impact the sort latency has on the full system cycle-level performance.
As another example, let's change our sort unit CL model to sort the four
input values in the reverse order. We can do this quite easily, by just
setting the reverse flag when calling Python's built-in sorted
function. Here is the updated concurrent block:
@s.tick_cl
def block():
s.pipe.append( deepcopy( [s.in_val] + sorted(s.in_, reverse=True ) ) )
data = s.pipe.popleft()
s.out_val.next = data[0]
for i, v in enumerate( data[1:] ):
s.out[i].next = vOf course we also need to update the test script to generate reference outputs where the values are in descending order. Once we make the changes to the test script, we can see the result as follows:
% cd $BUILDDIR
% py.test ../tut3_pymtl/sort/SortUnitCL_test.py -k test[2stage_stream] -s
2: {04,03,02,01}|
3: {09,06,07,01}|
4: {04,08,00,09}|{04,03,02,01}
5: |{09,07,06,01}
6: |{09,08,04,00}
As expected, the output values are now in descending order. The key idea is that experimenting with different sort orders in an RTL model would require significantly more work than the quick change shown above. CL modeling can enable more productive design-space exploration of cycle-level performance.
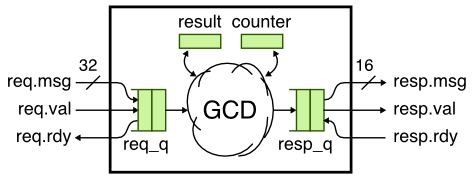
We now review the GCD unit CL model also introduced in the PyMTL tutorial and shown in the following figure. Unlike the sort unit CL model, here we want to model an iterative microarchitecture. In this case we can simply do the GCD immediately in a single cycle and then use a counter to wait a certain number of cycles. The number of cycles to wait should roughly approximate how long the real hardware will require to calculate the GCD.
Here is the code used to estimate the number of cycles:
def gcd( a, b ):
ncycles = 0
while True:
ncycles += 1
if a < b:
a,b = b,a
elif b != 0:
a = a - b
else:
return (a,ncycles)Take a look at how the CL model uses adapters to simplify interfacing
with the latency insensitive val/rdy interface. Instead of having to
directly read and write the val/rdy ports, a CL model can call deq
(dequeue) and enq (enqueue) methods on the adapters to receive or send
messages on val/rdy interfaces. Let's run the GCD unit CL tests and then
produce a line trace:
% cd $BUILDDIR
% py.test ../tut3_pymtl/gcd/GcdUnitCL_test.py
% py.test ../tut3_pymtl/gcd/GcdUnitCL_test.py -k test[basic_0x0] -s
2: > (). > .
3: 000f:0005 > 000f:0005() >
4: 0003:0009 > 0003:0009() >
5: # > # () >
6: # > # () >
7: # > # () >
8: # > # () >
9: # > # ()0005 > 0005
10: 0000:0000 > 0000:0000() >
11: # > # () >
12: # > # () >
13: # > # () >
14: # > # () >
15: # > # () >
16: # > # ()0003 > 0003
17: 001b:000f > 001b:000f() >
18: # > # ()0000 > 0000
19: 0015:0031 > 0015:0031() >
20: # > # () >
21: # > # () >
22: # > # () >
23: # > # () >
24: # > # () >
25: # > # () >
26: # > # () >
27: # > # () >
28: # > # () >
29: # > # ()0003 > 0003
Now let's assume we want to experiment with the impact of a hardware optimization that combines the swap and subtract operation into a single step. We simply need to change the code that estimates the number of cycles to something like this:
def gcd( a, b ):
ncycles = 0
while True:
ncycles += 1
if a < b:
a,b = b-a,a
elif b != 0:
a = a - b
else:
return (a,ncycles)Notice how we now also do a subtraction at the same time we swap a and
b. The resulting line trace is now:
2: > (). > .
3: 000f:0005 > 000f:0005() >
4: 0003:0009 > 0003:0009() >
5: # > # () >
6: # > # () >
7: # > # () >
8: # > # () >
9: # > # ()0005 > 0005
10: 0000:0000 > 0000:0000() >
11: # > # () >
12: # > # () >
13: # > # () >
14: # > # () >
15: # > # ()0003 > 0003
16: 001b:000f > 001b:000f() >
17: # > # ()0000 > 0000
18: 0015:0031 > 0015:0031() >
19: # > # () >
20: # > # () >
21: # > # () >
22: # > # () >
23: # > # () >
24: # > # () >
25: # > # () >
26: # > # ()0003 > 0003
Our model now suggests the GCD unit will finish four transactions on cycle 26 instead of finishing on cycle 29. Conducting a similar experiment in an RTL model would require significant changes to the datapath and control unit, while experimenting with such cycle-level behavior in a CL model is much easier.
We now examine a more involved CL model for a specific target cache
design. The target cache includes cachereq/cacheresp interfaces for
the unit that wants to use the cache, and memreq/memresp interfaces
for connecting the cache to main memory. We will be modeling a relatively
simple cache that is direct-mapped, write-through, and no-write-allocate.
The cache will have eight single-word cache lines and will only support
full-word cache requests. You can run all of the tests for the cache CL
model like this:
% cd $BUILDDIR
% py.test ../cache_cl
The sequential concurrent block for modeling the cycle-level behavior of the cache is shown below.
@s.tick_cl
def tick():
# Tick adapters
s.cachereq_q.xtick()
s.cacheresp_q.xtick()
s.memreq_q.xtick()
s.memresp_q.xtick()
# Some constants to simplify the code
s.READ = s.cache_ifc_dtypes.req.TYPE_READ
s.WRITE = s.cache_ifc_dtypes.req.TYPE_WRITE
# If we are not waiting for a memory response ...
if not s.wait_bit and not s.cachereq_q.empty() \
and not s.memreq_q.full() \
and not s.cacheresp_q.full():
cachereq = s.cachereq_q.deq()
if cachereq.type_ == s.WRITE : s.process_cachereq_write( cachereq )
elif cachereq.type_ == s.READ : s.process_cachereq_read ( cachereq )
else : assert False
# If we are waiting for a memory response ...
if s.wait_bit and not s.memresp_q.empty() \
and not s.cacheresp_q.full():
memresp = s.memresp_q.deq()
if memresp.type_ == s.WRITE : s.process_memresp_write( memresp )
elif memresp.type_ == s.READ : s.process_memresp_read ( memresp )
else : assert FalseAs with the GCD unit CL model, we use adapters on all four interfaces to
simplify interacting with the latency insensitive val/rdy microprotocol.
There are two primary parts to this concurrent block, and which part we
execute depends on the wait_bit. The wait_bit is true when we are
waiting for a memory response, and the wait_bit is false otherwise. If
we are not waiting for a memory response, then we check to see if there
is a new cache request (i.e., is the adapter for the cachereq interface
not empty?) but we also make sure that the memory request and cache
response interfaces are available. Note that this is somewhat
conservative; not all transactions need both the memory request and the
cache response (e.g., cache read hits do not need to send a memory
request), but we simplify our logic ensuring that all potentially
required resources are available before starting to process a cache
request. Based on the type of the cache request we dispatch to one of two
member functions. If we are waiting for a memory response, we again make
sure that all potentially required resources (i.e., the cache response
interface) are available before starting to process the memory response.
Based on the type of the memory response we dispatch to one of two member
functions. Take a closer look at how these four member functions are
implemented. Note how CL modeling is more of a software engineering
effort to model hardware as compared to RTL modeling which is more of a
hardware engineering effort to implement hardware. We can run a test and
view a line trace for the cache CL model like this:
% cd $BUILDDIR
% py.test ../cache_cl -k test_1port[basic] -s
# cachereq set 0 set 7 memreq memresp cacheresp
2: ( | ... | ) () .
3: wr:00:00001000:deadbeef ( | ... | ) ()
4: rd:01:00001000: ( | ... | ) wr:00:00001000:deadbeef()
5: . ( | ... | ) ()wr:00:0:
6: . ( | ... | ) () wr:00:0:
7: ( | ... | ) rd:01:00001000: ()
8: ( | ... | ) ()rd:01:0:deadbeef
9: (0000080| ... | ) () rd:01:0:deadbeef
We have replaced some of the line trace with ... to simplify the line
trace for this document. We have also added some extra annotation to
label the various columns. The line trace shows cache request/response,
memory request/response, as well as the tags for all eight cache lines.
The first write cache request is passed through to main memory because
this is a write-through cache. Since the cache is no-write-allocate, the
write cache request does not update the cache state, and the read cache
request misses. The read cache request eventually will update the cache
state with the data returned from main memory (notice how the tag 000080
is in set 0 at the beginning of cycle 9.
The basic_hit test includes a series of reads to the same cache line
and thus illustrates cache hits:
% cd $BUILDDIR
% py.test ../cache_cl -k test_1port[basic_hit] -s
# cachereq set 0 memreq memresp cacheresp
2: ( | ... ) ( ) .
3: wr:00:00001000:deadbeef ( | ... ) ( )
4: rd:01:00001000: ( | ... ) wr:00:00001000:deadbeef( )
5: # ( | ... ) (* )
6: # ( | ... ) ( * )
7: # ( | ... ) ( * )
8: # ( | ... ) ( * )
9: # ( | ... ) ( *)
10: # ( | ... ) ( )wr:00:0:
11: # ( | ... ) ( ) wr:00:0:
12: wr:02:00001000:deadbeef ( | ... ) rd:01:00001000: ( )
13: # ( | ... ) (* )
14: # ( | ... ) ( * )
15: # ( | ... ) ( * )
16: # ( | ... ) ( * )
17: # ( | ... ) ( *)
18: # ( | ... ) ( )rd:01:0:deadbeef
19: # (0000080| ... ) ( ) rd:01:0:deadbeef
20: rd:03:00001000: (0000080| ... ) wr:02:00001000:deadbeef( )
21: # (0000080| ... ) (* )
22: # (0000080| ... ) ( * )
23: # (0000080| ... ) ( * )
24: # (0000080| ... ) ( * )
25: # (0000080| ... ) ( *)
26: # (0000080| ... ) ( )wr:02:0:
27: # (0000080| ... ) ( ) wr:02:0:
28: rd:04:00001000: (0000080| ... ) ( ) rd:03:0:deadbeef
29: rd:05:00001000: (0000080| ... ) ( ) rd:04:0:deadbeef
30: rd:06:00001000: (0000080| ... ) ( ) rd:05:0:deadbeef
31: (0000080| ... ) ( ) rd:06:0:deadbeef
Notice how this test uses a test memory with a latency of five cycles. The later reads hit in the cache. They do not require memory requests and are returned with a single-cycle hit latency. After looking at the code, it should hopefully be clear how it would be possible to modify the cache CL model to flexibly model a variety of caches with different cache line sizes, cache capacities, write policies, and replacement policies. Creating these kind of highly parameterized models is much easier when working with CL modeling as as compared to RTL modeling.
Let's modify our cache CL model to use a write-allocate policy. We simply
need to change the process_cachereq_write member function to update the
cache state on a write miss. The required changes are shown below:
def process_cachereq_write( s, cachereq ):
# Check to see if we hit or miss in cache
tag = cachereq.addr[5:32]
idx = cachereq.addr[2:5]
hit = s.cache[idx].valid and (s.cache[idx].tag == tag)
# On a cache hit, update the corresponding data
if hit:
s.cache[idx].data = cachereq.data
# On a cache miss, update the valid bit, tag, and data
if not hit:
cache_line = CacheLine()
cache_line.valid = True
cache_line.tag = tag
cache_line.data = cachereq.data
s.cache[idx] = cache_line
# Always send write request to main memory
s.memreq_q.enq( cachereq )
# Set wait bit so cache knows to wait for response message
s.wait_bit = TrueIf we rerun the basic_hit test we should see the data being allocated
in the cache on the very first write cache request.
% cd $BUILDDIR
% py.test ../cache_cl -k test_1port[basic_hit] -s
# cachereq set 0 memreq memresp cacheresp
2: ( | ... ) ( ) .
3: wr:00:00001000:deadbeef ( | ... ) ( )
4: rd:01:00001000: (0000080| ... ) wr:00:00001000:deadbeef( )
5: # (0000080| ... ) (* )
6: # (0000080| ... ) ( * )
7: # (0000080| ... ) ( * )
8: # (0000080| ... ) ( * )
9: # (0000080| ... ) ( *)
10: # (0000080| ... ) ( )wr:00:0:
11: # (0000080| ... ) ( ) wr:00:0:
12: wr:02:00001000:deadbeef (0000080| ... ) ( ) rd:01:0:deadbeef
13: rd:03:00001000: (0000080| ... ) wr:02:00001000:deadbeef( )
14: # (0000080| ... ) (* )
15: # (0000080| ... ) ( * )
16: # (0000080| ... ) ( * )
17: # (0000080| ... ) ( * )
18: # (0000080| ... ) ( *)
19: # (0000080| ... ) ( )wr:02:0:
20: # (0000080| ... ) ( ) wr:02:0:
21: rd:04:00001000: (0000080| ... ) ( ) rd:03:0:deadbeef
22: rd:05:00001000: (0000080| ... ) ( ) rd:04:0:deadbeef
23: rd:06:00001000: (0000080| ... ) ( ) rd:05:0:deadbeef
24: (0000080| ... ) ( ) rd:06:0:deadbeef
Compare this line trace to the previous line trace and notice how the first read cache request now hits in the cache. Experimenting with changing the write policy in an RTL model would likely require significant changes to the datapath and the control unit, while this experiment is relatively simple to implement in a CL model. If we were evaluating a full system where this cache was just one component, we could use our CL model to help understand the system-level performance impact of no-write-allocate vs. write-allocate, and this would guide us to a promising design before we even write one line of RTL code.
As another example, let's assume we wish to model a cache with a two cycle instead of single cycle hit latency. All we need to do is buffer the cache response for one extra cycle. First, we add this buffer in the constructor of our cache CL model:
# Extra buffering to model two-cycle hit latency
s.pipebuf = NoneNow we need to modify the process_cachereq_read member function as
follows to place the cache response in this new buffer instead of
immediately sending the cache response out the cacheresp interface.
def process_cachereq_read( s, cachereq ):
# Check to see if we hit or miss in cache
tag = cachereq.addr[5:32]
idx = cachereq.addr[2:5]
hit = s.cache[idx].valid and (s.cache[idx].tag == tag)
# On a cache hit, return data from cache
if hit:
cacheresp = s.cache_ifc_dtypes.resp
cacheresp.type_ = s.cache_ifc_dtypes.resp.TYPE_READ
cacheresp.opaque = cachereq.opaque
cacheresp.len = cachereq.len
cacheresp.data = s.cache[idx].data
s.pipebuf = cacheresp
# On a cache miss, send out refill request to main memory
if not hit:
s.memreq_q.enq( cachereq )
# Set wait bit so cache knows to wait for response message.
s.wait_bit = True
s.wait_addr = cachereq.addrFinally, in the tick_cl function we need to copy the cache response
from the pipebuf and send it out the cacheresp interface. Try adding
this code at the end of the tick_cl function:
if s.pipebuf:
s.cacheresp_q.enq( s.pipebuf )
s.pipebuf = NoneEvery cycle we check to see if there is anything in the s.pipebuf
(i.e., is the s.pipebuf not None) and if there is indeed something
waiting in the s.pipebuf we send it out the cacheresp interface. We
clear the s.pipebuf so we know that we are done with this response. If
you rerun the basic_hit test, the end of the line trace should look
like this:
% cd $BUILDDIR
% py.test ../cache_cl -k test_1port[basic_hit] -s
# cachereq set 0 memreq memresp cacheresp
21: rd:04:00001000: (0000080| ... ) ( ) rd:03:0:deadbeef
22: rd:05:00001000: (0000080| ... ) ( ) rd:04:0:deadbeef
23: rd:06:00001000: (0000080| ... ) ( ) rd:05:0:deadbeef
24: (0000080| ... ) ( ) rd:06:0:deadbeef
Nothing has changed! Read hits still take a single cycle. The problem is
that the process_cachereq_read member function is called first in the
s.tick_cl, we write the s.pipebuf, and then at the end of the
s.tick_cl we send the cache response out the cacheresp interface. We
need to place the code that sends the cache response out the cacheresp
interface at the beginning of the s.tick_cl (well after the calls to
xtick but before we process any cache requests or memory responses).
With this change you should see the following line trace:
% cd $BUILDDIR
% py.test ../cache_cl -k test_1port[basic_hit] -s
# cachereq set 0 memreq memresp cacheresp
22: rd:04:00001000: (0000080| ... ) ( )
23: # (0000080| ... ) ( ) rd:03:0:deadbeef
24: rd:05:00001000: (0000080| ... ) ( )
25: # (0000080| ... ) ( ) rd:04:0:deadbeef
26: rd:06:00001000: (0000080| ... ) ( )
27: . (0000080| ... ) ( ) rd:05:0:deadbeef
28: (0000080| ... ) ( )
29: (0000080| ... ) ( ) rd:06:0:deadbeef
This is still not correct. Now a cache read hit is taking three cycles
and it looks like there is some extra occupancy instead of the
full-throughput pipeline behavior we were hoping for. The problem now is
that our s.tick_cl function is still checking to see if the cacheresp
interface is ready; we should really be checking to see if the
s.pipebuf is empty or not. The final correct s.tick_cl implementation
should look like this:
@s.tick_cl
def tick():
# Tick adapters
s.cachereq_q.xtick()
s.cacheresp_q.xtick()
s.memreq_q.xtick()
s.memresp_q.xtick()
# Some constants to simplify the code
s.READ = s.cache_ifc_dtypes.req.TYPE_READ
s.WRITE = s.cache_ifc_dtypes.req.TYPE_WRITE
# Model an extra cycle of latency for read hits
if s.pipebuf:
s.cacheresp_q.enq( s.pipebuf )
s.pipebuf = None
# If we are not waiting for a memory response ...
# Notice that we check s.pipebuf not s.cacheresp_q.full()
if not s.wait_bit and not s.cachereq_q.empty() \
and not s.memreq_q.full() \
and not s.pipebuf:
cachereq = s.cachereq_q.deq()
if cachereq.type_ == s.WRITE : s.process_cachereq_write( cachereq )
elif cachereq.type_ == s.READ : s.process_cachereq_read ( cachereq )
else : assert False
# If we are waiting for a memory response ...
if s.wait_bit and not s.memresp_q.empty() \
and not s.cacheresp_q.full():
memresp = s.memresp_q.deq()
if memresp.type_ == s.WRITE : s.process_memresp_write( memresp )
elif memresp.type_ == s.READ : s.process_memresp_read ( memresp )
else : assert FalseAnd the resulting line trace should look like this:
% cd $BUILDDIR
% py.test ../cache_cl -k test_1port[basic_hit] -s
# cachereq set 0 memreq memresp cacheresp
21: rd:04:00001000: (0000080| ... ) ( )
22: rd:05:00001000: (0000080| ... ) ( ) rd:03:0:deadbeef
23: rd:06:00001000: (0000080| ... ) ( ) rd:04:0:deadbeef
24: (0000080| ... ) ( ) rd:05:0:deadbeef
25: (0000080| ... ) ( ) rd:06:0:deadbeef
This is our desired cycle-level behavior. Cache read hits have a two cycle latency, yet we can still sustain full throughput. One of the key take-aways is that developing a CL model which does a reasonable job of modeling the cycle-level behavior can be challenging and often requires iteratively experimenting with small performance-focused test cases.
Most computer architects in industry and academia spend far more time developing CL models instead of RTL models. Computer architects will often start with a previously developed CL model and then experiment with new computer architecture ideas by modifying this CL model. A great example is the gem5 CL simulator. This simulator is written in C++ and includes detailed CL models for processors, memories, and networks. It includes complex processor CL models which model superscalar execution, out-of-order execution, register renaming, memory disambiguation, branch prediction, and speculative execution.
Here is an example of an assembly version of the vector-vector add microbenchmark running on the gem5 quad-issue out-of-order processor. The output from the simulator is post-processed to create a kind of pipeline view.
[fdn.ic...............r....................] 0x00808020.0 lw r6, 0(r2)
[fdn.pic..............r....................] 0x00808024.0 lw r7, 0(r3)
[fdn.p..............ic.r...................] 0x00808028.0 addu r8, r6, r7
[fdn.p...............ic.r..................] 0x0080802c.0 sw r8, 0(r4)
[.fdn.ic................r..................] 0x00808030.0 addiu r2, r2, 4
[.fdn.ic................r..................] 0x00808034.0 addiu r3, r3, 4
[.fdn.ic................r..................] 0x00808038.0 addiu r4, r4, 4
[.fdn..ic................r.................] 0x0080803c.0 addiu r5, r5, 1
[..fdn..ic...............r.................] 0x00808040.0 bne r5, r1, 0x808020
[...f..dn.ic.............r.................] 0x00808020.0 lw r6, 0(r2)
[...f..dn.pic............r.................] 0x00808024.0 lw r7, 0(r3)
[...f..dn.p.........ic....r................] 0x00808028.0 addu r8, r6, r7
[...f..dn.p...........ic..r................] 0x0080802c.0 sw r8, 0(r4)
[.......fdn.ic............r................] 0x00808030.0 addiu r2, r2, 4
[.......fdn.ic............r................] 0x00808034.0 addiu r3, r3, 4
[.......fdn.ic.............r...............] 0x00808038.0 addiu r4, r4, 4
[.......fdn.ic.............r...............] 0x0080803c.0 addiu r5, r5, 1
[........fdn.pic...........r...............] 0x00808040.0 bne r5, r1, 0x808020
Here is the legend:
f= fetch stage,d= decode stage,n= rename stage.after n is always an extra "ROB allocation" stagep= "dispatch", we think this is similar to how we show an i when an instruction goes into the IQc= complete stage, this seems to be the same as an X stagei= issue stage, for long latency operations the "latency" happens while the instruction is in the issue queue and then you see theiat the end right before the instruction is complete. so you will not see more than oneiorcfor a long latency instruction.after c stage, we think this is similar to our W stager= retire stage, this is similar to our C stage
Here is the above pipeline view carefully transformed into a pipeline diagram similar in spirit to what we learned in ECE 4750.
0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6
----------------------------------------------------------------------
lw r6, 0(r2) F D N R I X q . . . . . . . . . . M W r . C lw -> LSQ, D$ miss, resp on cyc 17 in M
lw r7, 0(r3) F D N R i I X q . . . . . . . . . . M W r C lw -> LSQ, D$ miss, resp on cyc 17 in M
addu r8, r6, r7 F D N R i . . . . . . . . . . . . . . I X W C RAW hazard, addu waits in IQ for lw insts
sw r8, 0(r4) F D N R i . . . . . . . . . . . . . . . I X W C RAW hazard, sw waits in IQ for addu
addiu r2, r2, 4 F D N R I X W r . . . . . . . . . . . . . . C
addiu r3, r3, 4 F D N R I X W r . . . . . . . . . . . . . . C
addiu r4, r4, 4 F D N R I X W r . . . . . . . . . . . . . . C
addiu r5, r5, 1 F D N R i I X W r . . . . . . . . . . . . . . C struct hazard, only 4 issue ports
bne r5, r1, loop F D N R i I X W r . . . . . . . . . . . . . C RAW hazard, bne waits in IQ for addiu r5
----------------------------------------------------------------------
lw r6, 0(r2) F D D D N R I X q . . . . . M W r . . . . C struct hazard, lw waits since LSQ is full
lw r7, 0(r3) F D D D N R i I X q . . . . . M W r . . . C struct hazard, lw waits since LSQ is full
addu r8, r6, r7 F D D D N R i . . . . . . . . . I X W r . . C above struct hazard -> whole bundle stalls
sw r8, 0(r4) F D D D N R i . . . . . . . . . . . I X W r C above struct hazard -> whole bundle stalls
addiu r2, r2, 4 F F F F D N R I X W r . . . . . . . . . . C stalls because prev bundle stallling in D
addiu r3, r3, 4 F F F F D N R I X W r . . . . . . . . . . C stalls because prev bundle stallling in D
addiu r4, r4, 4 F F F F D N R I X W r . . . . . . . . . . . C stalls because prev bundle stallling in D
addiu r5, r5, 1 F F F F D N R I X W r . . . . . . . . . . . C stalls because prev bundle stallling in D
bne r5, r1, loop F D N R i I X W r . . . . . . . . . C why does bne wait in IQ one cycle?
And here is the legend:
F: fetchD: decodeN: renameR: ROB allocationI: issueX: execute for arithmetic operationsM: memory access completion for ld/st operationsW: writebackC: commiti: waiting in issue queuer: waiting in ROBq: waiting in LSQ for memory response to come back
From the pipeline diagram we can see how the CL model is capturing many of the complex features we learned in ECE 4750. It is faithfully tracking RAW hazards and structural hazards, and it is modeling cache effects, aggressive branch prediction, and fully out-of-order load/store issue. Implementing this kind of processor in RTL would require a tremendous design team and would never be as flexible and extensible as the gem5 CL simulator, which is why architects usually prefer CL models when doing early design-space exploration. Of course, the challenge with a CL model is it is possible to model completely unrealistic hardware, and it is very challenging to estimate the area, energy, and timing of a specific design. So in this course, we argue for a balanced approach that uses a mix of FL, CL, and RTL modeling.