In-memory immutable 2D R-tree implementation in java using RxJava Observables for reactive processing of search results.
Status: released to Maven Central, ensure you use at least 0.4 to get fix for #7
An R-tree is a commonly used spatial index.
This was fun to make, has an elegant concise algorithm, is thread-safe and fast.
The algorithm to achieve immutability is cute. For insertion/deletion it involves recursion down to the required leaf node then recursion back up to replace the parent nodes up to the root. The guts of it is in Leaf.java and NonLeaf.java.
Backpressure support required some complexity because effectively a bookmark needed to be kept for a position in the tree and returned to later to continue traversal. An immutable stack containing the node and child index of the path nodes came to the rescue here and recursion was abandoned in favour of looping to prevent stack overflow (unfortunately java doesn't support tail recursion!).
Maven site reports are here including javadoc.
- immutable R-tree suitable for concurrency
- Guttman's heuristics (Quadratic splitter) (paper)
- R*-tree heuristics (paper)
- Customizable splitter and selector
- search returns
Observable - search is cancelled by unsubscription
- search is
O(log(n))on average - insert, delete are
O(n)worst case - all search methods return lazy-evaluated streams offering efficiency and flexibility of functional style including functional composition and concurrency
- balanced delete
- uses structural sharing
- supports backpressure
- JMH benchmarks
- visualizer included
- 100% unit test code coverage
- R*-tree performs 530,000 searches/second returning 22 entries from a tree of 38,377 Greek earthquake locations on i7-920@2.67Ghz (maxChildren=4, minChildren=4). Insert at 135,000 entries per second.
- requires java 1.6 or later
Number of points = 1000, max children per node 8:
| Quadratic split | R*-tree split |
|---|---|
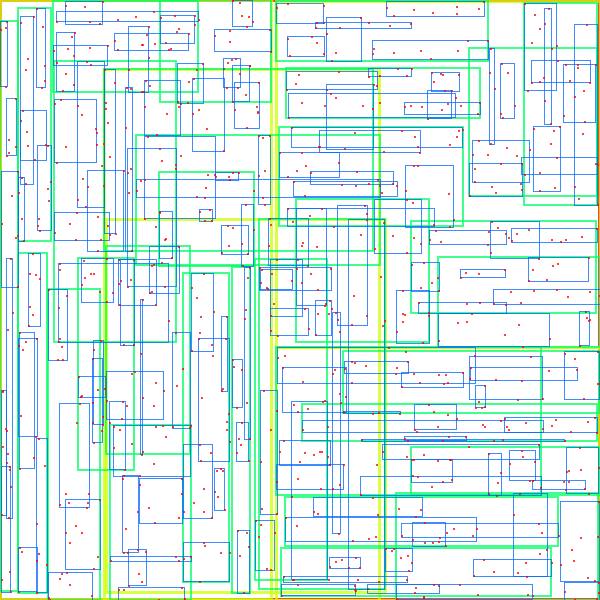 |
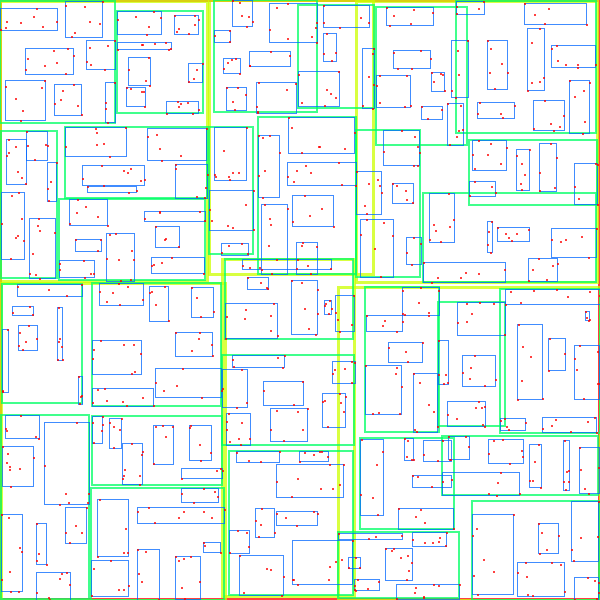 |
Notice that there is little overlap in the R*-tree split compared to the Quadratic split. This should provide better search performance (and in general benchmarks show this).
Add this maven dependency to your pom.xml:
<dependency>
<groupId>com.github.davidmoten</groupId>
<artifactId>rtree</artifactId>
<version>0.6.1</version>
</dependency>###Instantiate an R-Tree
Use the static builder methods on the RTree class:
// create an R-tree using Quadratic split with max
// children per node 4, min children 2 (the threshold
// at which members are redistributed)
RTree<String, Geometry> tree = RTree.create();You can specify a few parameters to the builder, including minChildren, maxChildren, splitter, selector:
RTree<String, Geometry> tree = RTree.�minChildren(3).maxChildren(6).create();###Generic typing
If for instance you know that the entry geometry is always Point then create an RTree specifying that generic type to gain more type safety:
RTree<String, Point> tree = RTree.create();###R*-tree If you'd like an R*-tree (which uses a topological splitter on minimal margin, overlap area and area and a selector combination of minimal area increase, minimal overlap, and area):
RTree<String, Geometry> tree = RTree.star().maxChildren(6).create();
See benchmarks below for some of the performance differences.
###Add items to the R-tree
When you add an item to the R-tree you need to provide a geometry that represents the 2D physical location or
extension of the item. The Geometries builder provides these factory methods:
Geometries.rectangleGeometries.circleGeometries.point
To add an item to an R-tree:
RTree<T,Geometry> tree = RTree.create();
tree = tree.add(item, Geometries.point(10,20));or
tree = tree.add(Entry.entry(item, Geometries.point(10,20));Important note: being an immutable data structure, calling tree.add(item, geometry) does nothing to tree,
it returns a new RTree containing the addition. Make sure you use the result of the add!
###Remove an item in the R-tree To remove an item from an R-tree, you need to match the item and its geometry:
tree = tree.delete(item, Geometries.point(10,20));or
tree = tree.delete(entry);Important note: being an immutable data structure, calling tree.delete(item, geometry) does nothing to tree,
it returns a new RTree without the deleted item. Make sure you use the result of the delete!
###Custom geometries
You can also write your own implementation of Geometry. An implementation of Geometry needs to specify methods to:
- check intersection with a rectangle (you can reuse the distance method here if you want but it might affect performance)
- provide a minimum bounding rectangle
- implement
equalsandhashCodefor consistent equality checking - measure distance to a rectangle (0 means they intersect). Note that this method is only used for search within a distance so implementing this method is optional. If you don't want to implement this method just throw a
RuntimeException.
For the R-tree to be well-behaved, the distance function if implemented needs to satisfy these properties:
distance(r) >= 0 for all rectangles rif rectangle r1 contains r2 then distance(r1)<=distance(r2)distance(r) = 0 if and only if the geometry intersects the rectangle r
###Searching
The advantage of an R-tree is the ability to search for items in a region reasonably quickly.
On average search is O(log(n)) but worst case is O(n).
Search methods return Observable sequences:
Observable<Entry<T, Geometry>> results =
tree.search(Geometries.rectangle(0,0,2,2));or search for items within a distance from the given geometry:
Observable<Entry<T, Geometry>> results =
tree.search(Geometries.rectangle(0,0,2,2),5.0);To return all entries from an R-tree:
Observable<Entry<T, Geometry>> results = tree.entries();Suppose you make a custom geometry like Polygon and you want to search an RTree<String,Point> for points inside the polygon. This is how you do it:
RTree<String, Point> tree = RTree.create();
Func2<Point, Polygon, Boolean> pointInPolygon = ...
Polygon polygon = ...
...
entries = tree.search(polygon, pointInPolygon);The key is that you need to supply the intersects function (pointInPolygon) to the search. It is on you to implement that for all types of geometry present in the RTree. This is one reason that the generic Geometry type was added in rtree 0.5 (so the type system could tell you what geometry types you needed to calculate intersection for) .
As per the example above to do a proximity search you need to specify how to calculate distance between the geometry you are searching and the entry geometries:
RTree<String, Point> tree = RTree.create();
Func2<Point, Polygon, Boolean> distancePointToPolygon = ...
Polygon polygon = ...
...
entries = tree.search(polygon, 10, distancePointToPolygon);import com.github.davidmoten.rtree.RTree;
import static com.github.davidmoten.rtree.geometry.Geometries.*;
RTree<String, Point> tree = RTree.maxChildren(5).create();
tree = tree.add("DAVE", point(10, 20))
.add("FRED", point(12, 25))
.add("MARY", point(97, 125));
Observable<Entry<String, Point>> entries =
tree.search(Rectangle.create(8, 15, 30, 35));See LatLongExampleTest.java for an example. The example depends on grumpy-core artifact which is also on Maven Central.
See LatLongExampleTest.testSearchLatLongCircles() for an example of searching circles around geographic points (using great circle distance).
Very useful, see RxJava.
As an example, suppose you want to filter the search results then apply a function on each and reduce to some best answer:
import rx.Observable;
import rx.functions.*;
import rx.schedulers.Schedulers;
Func1<Entry<String, Geometry>, Character> firstCharacter =
entry -> entry.value().charAt(0);
Func2<Character,Character,Character> firstAlphabetically
= (x,y) -> x <=y ? x : y;
Character result =
tree.search(Geometries.rectangle(8, 15, 30, 35))
// filter for names alphabetically less than M
.filter(entry -> entry.value() < "M")
// get the first character of the name
.map(entry -> firstCharacter(entry.value()))
// reduce to the first character alphabetically
.reduce((x,y) -> firstAlphabetically(x,y))
// subscribe to the stream and block for the result
.toBlocking().single();
System.out.println(list);output:
D
Check out the benchmarks below, but I recommend you do your own benchmarks because every data set will behave differently. If you don't want to benchmark then use the defaults. General rules based on the benchmarks:
- for data sets of <10,000 entries use the default R-tree (quadratic splitter with maxChildren=4)
- for data sets of >=10,000 entries use the star R-tree (R*-tree heuristics with maxChildren=4 by default)
Watch out though, the benchmark data sets had quite specific characteristics. The 1000 entry dataset was randomly generated (so is more or less uniformly distributed) and the Greek dataset was earthquake data with its own clustering characteristics.
If you are not familiar with the Observable API and want to skip the reactive stuff then here's how to get an Iterable from a search:
Iterable<T> it = tree.search(Geometries.point(4,5))
.toBlocking().toIterable();The backpressure slow path may be enabled by some RxJava operators. This may slow search performance by a factor of 3 but avoids possible out of memory errors and thread starvation due to asynchronous buffering. Backpressure is benchmarked below.
To visualize the R-tree in a PNG file of size 600 by 600 pixels just call:
tree.visualize(600,600)
.save("target/mytree.png");The result is like the images in the Features section above.
The RTree.asString() method returns output like this:
mbr=Rectangle [x1=10.0, y1=4.0, x2=62.0, y2=85.0]
mbr=Rectangle [x1=28.0, y1=4.0, x2=34.0, y2=85.0]
entry=Entry [value=2, geometry=Point [x=29.0, y=4.0]]
entry=Entry [value=1, geometry=Point [x=28.0, y=19.0]]
entry=Entry [value=4, geometry=Point [x=34.0, y=85.0]]
mbr=Rectangle [x1=10.0, y1=45.0, x2=62.0, y2=63.0]
entry=Entry [value=5, geometry=Point [x=62.0, y=45.0]]
entry=Entry [value=3, geometry=Point [x=10.0, y=63.0]]
This library has a dependency on guava 18.0 which is about 2.2M. If you are coding for Android you may want to use ProGuard to trim
the final application size. The dependency is driven by extensive use of Optional,Preconditions,Objects, and the use of
MinMaxPriorityQueue for the nearest-k search. I'm open to the possibility of internalizing these dependencies if people care
about the dependency size a lot. Let me know.
git clone https://github.com/davidmoten/rtree.git
cd rtree
mvn clean install
Benchmarks are provided by
mvn clean install -Pbenchmark
This codebase is scanned by Coverity scan whenever the branch coverity_scan is updated.
For the project committers if a coverity scan is desired just do this:
git checkout coverity_scan
git pull origin master
git push origin coverity_scanThe Greek data referred to in the benchmarks is a collection of some 38,377 entries corresponding to the epicentres of earthquakes in Greece between 1964 and 2000. This data set is used by multiple studies on R-trees as a test case.
These were run on i7-920@2.67GHz with rtree version 0.6.1:
Benchmark Mode Samples Score Error Units
c.g.d.r.BenchmarksRTree.defaultRTreeInsertOneEntryInto1000EntriesMaxChildren004 thrpt 10 170629.988 ± 1992.468 ops/s
c.g.d.r.BenchmarksRTree.defaultRTreeInsertOneEntryInto1000EntriesMaxChildren010 thrpt 10 199225.527 ± 3687.661 ops/s
c.g.d.r.BenchmarksRTree.defaultRTreeInsertOneEntryInto1000EntriesMaxChildren032 thrpt 10 92269.915 ± 1777.963 ops/s
c.g.d.r.BenchmarksRTree.defaultRTreeInsertOneEntryInto1000EntriesMaxChildren128 thrpt 10 282006.364 ± 4718.936 ops/s
c.g.d.r.BenchmarksRTree.defaultRTreeInsertOneEntryIntoGreekDataEntriesMaxChildren004 thrpt 10 178533.217 ± 1397.901 ops/s
c.g.d.r.BenchmarksRTree.defaultRTreeInsertOneEntryIntoGreekDataEntriesMaxChildren010 thrpt 10 211693.060 ± 2160.555 ops/s
c.g.d.r.BenchmarksRTree.defaultRTreeInsertOneEntryIntoGreekDataEntriesMaxChildren032 thrpt 10 147575.589 ± 1309.416 ops/s
c.g.d.r.BenchmarksRTree.defaultRTreeInsertOneEntryIntoGreekDataEntriesMaxChildren128 thrpt 10 81962.980 ± 1114.323 ops/s
c.g.d.r.BenchmarksRTree.defaultRTreeSearchOf1000PointsMaxChildren004 thrpt 10 841284.193 ± 12172.013 ops/s
c.g.d.r.BenchmarksRTree.defaultRTreeSearchOf1000PointsMaxChildren010 thrpt 10 331521.896 ± 15179.039 ops/s
c.g.d.r.BenchmarksRTree.defaultRTreeSearchOf1000PointsMaxChildren032 thrpt 10 339449.893 ± 1768.640 ops/s
c.g.d.r.BenchmarksRTree.defaultRTreeSearchOf1000PointsMaxChildren128 thrpt 10 430664.624 ± 7939.214 ops/s
c.g.d.r.BenchmarksRTree.defaultRTreeSearchOfGreekDataPointsMaxChildren004 thrpt 10 332686.163 ± 7647.466 ops/s
c.g.d.r.BenchmarksRTree.defaultRTreeSearchOfGreekDataPointsMaxChildren010 thrpt 10 213191.627 ± 2998.905 ops/s
c.g.d.r.BenchmarksRTree.defaultRTreeSearchOfGreekDataPointsMaxChildren032 thrpt 10 122136.799 ± 3024.498 ops/s
c.g.d.r.BenchmarksRTree.defaultRTreeSearchOfGreekDataPointsMaxChildren128 thrpt 10 49765.765 ± 391.503 ops/s
c.g.d.r.BenchmarksRTree.rStarTreeDeleteOneEveryOccurrenceFromGreekDataChildren010 thrpt 10 195698.148 ± 1650.701 ops/s
c.g.d.r.BenchmarksRTree.rStarTreeInsertOneEntryInto1000EntriesMaxChildren004 thrpt 10 155788.206 ± 1976.180 ops/s
c.g.d.r.BenchmarksRTree.rStarTreeInsertOneEntryInto1000EntriesMaxChildren010 thrpt 10 143670.205 ± 1525.071 ops/s
c.g.d.r.BenchmarksRTree.rStarTreeInsertOneEntryInto1000EntriesMaxChildren032 thrpt 10 37517.491 ± 634.409 ops/s
c.g.d.r.BenchmarksRTree.rStarTreeInsertOneEntryInto1000EntriesMaxChildren128 thrpt 10 116450.918 ± 1461.198 ops/s
c.g.d.r.BenchmarksRTree.rStarTreeInsertOneEntryIntoGreekDataEntriesMaxChildren004 thrpt 10 135777.256 ± 1003.535 ops/s
c.g.d.r.BenchmarksRTree.rStarTreeInsertOneEntryIntoGreekDataEntriesMaxChildren010 thrpt 10 108184.558 ± 1210.154 ops/s
c.g.d.r.BenchmarksRTree.rStarTreeInsertOneEntryIntoGreekDataEntriesMaxChildren032 thrpt 10 31833.529 ± 349.885 ops/s
c.g.d.r.BenchmarksRTree.rStarTreeInsertOneEntryIntoGreekDataEntriesMaxChildren128 thrpt 10 3884.568 ± 34.335 ops/s
c.g.d.r.BenchmarksRTree.rStarTreeSearchOf1000PointsMaxChildren004 thrpt 10 438527.764 ± 5882.232 ops/s
c.g.d.r.BenchmarksRTree.rStarTreeSearchOf1000PointsMaxChildren010 thrpt 10 707710.764 ± 13940.099 ops/s
c.g.d.r.BenchmarksRTree.rStarTreeSearchOf1000PointsMaxChildren032 thrpt 10 426923.809 ± 6349.023 ops/s
c.g.d.r.BenchmarksRTree.rStarTreeSearchOf1000PointsMaxChildren128 thrpt 10 698529.029 ± 9430.641 ops/s
c.g.d.r.BenchmarksRTree.rStarTreeSearchOfGreekDataPointsMaxChildren004 thrpt 10 531461.541 ± 8004.566 ops/s
c.g.d.r.BenchmarksRTree.rStarTreeSearchOfGreekDataPointsMaxChildren010 thrpt 10 407222.646 ± 4319.595 ops/s
c.g.d.r.BenchmarksRTree.rStarTreeSearchOfGreekDataPointsMaxChildren010WithBackpressure thrpt 10 109341.392 ± 1624.047 ops/s
c.g.d.r.BenchmarksRTree.rStarTreeSearchOfGreekDataPointsMaxChildren032 thrpt 10 359887.451 ± 2771.129 ops/s
c.g.d.r.BenchmarksRTree.rStarTreeSearchOfGreekDataPointsMaxChildren128 thrpt 10 247366.614 ± 3056.753 ops/s