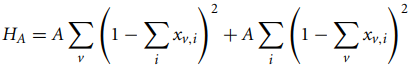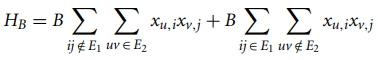This demonstration addresses the task of verifying the equivalence of two representations of the design of an electronic circuit, which is of interest in the field of electronic design automation. By converting the representation of each circuit into a graph, the problem can be reduced to that of determining whether the two graphs are isomorphic. The two graphs are said to be isomorphic if there is a one-to-one-correspondence between the vertex sets such that the adjacency relationships are identical. Graph isomorphism is a problem of general interest, and it is not currently known whether it is NP complete [1].
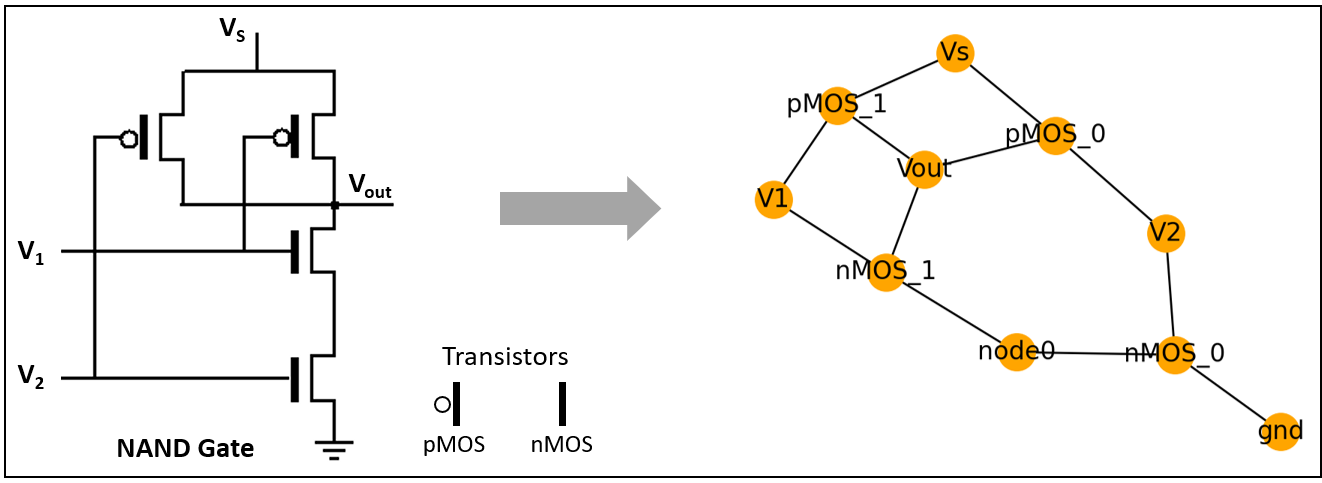
The following figure depicts the schematic representation of a CMOS NAND gate, along with the corresponding graph:
To run the demonstration, execute:
python equivalence.py --show-plotOr:
python equivalence.py --save-plotEither of these commands solves the circuit equivalence problem for two
different descriptions of a CMOS NAND gate (provided in the cmos_nand_1.txt
and cmos_nand2.txt files in the netlists directory). Other circuit
descriptions may be used as input by providing them as positional arguments in
the execution command. The --show-plot and --save-plot flags are optional,
and they generate a plot of the graphs of the two circuits, using colors to
indicate the identified node correspondence. The --show-plot flag displays an
interactive plot using matplotlib, and --save-plot saves the plot to a file.
Run python equivalence.py -h for a description of the command line options.
The code uses the following steps:
- Each of the two netlist files specified on the command line (or the default example files) is parsed, constructing a list of components for each of the two circuit descriptions.
- Each circuit is then converted into a graph where each element in the circuit is represented by a node in the graph, and edges are used to represent connections between the elements in the circuit.
- Next, a discrete quadratic model (DQM) is constructed such that the objective function represents the problem of finding an isomorphism between the two graphs. Further details are given in the next section.
- The DQM is then solved on the hybrid quantum-classical computing resource using the LeapHybridDQMSampler.
- Each result in the SampleSet is then checked to determine whether (a) it indicates an isomorphism and (b) the identified isomorphism represents equivalent circuits (e.g., that a pMOS transistor in the first circuit is mapped to a pMOS transistor in the second).
The code is set up to read circuit definitions from
netlist files in a simple text format.
Several example netlist files are provided in the netlists directory:
cmos_nand_1.txt: Specification of a CMOS NAND gatecmos_nand_2.txt: Alternative specification of a CMOS NAND gate, using only small changes in the naming of the components and the ordering of the definitions, relative tocmos_nand_1.txtcmos_nand_error.txt: An example of an incorrect specification of a CMOS NAND gate, which is not equivalent to the correct representationcmos_nor_1.txt: Specification of a CMOS NOR gate. This circuit does produce a graph that is isomorphic with that of the CMOS NAND gate, but with the pMOS and nMOS transistors swapped. The example code checks for matches in the transistor types of corresponding nodes identified by the graph isomorphism, so it should determine that the NAND and NOR gate netlists are not equivalent.
When the netlist files are not explicitly named on the command line, the program
defaults to using cmos_nand_1.txt and cmos_nand_2.txt.
The core part of the code involves formulating the graph isomorphism problem as
a discrete quadratic model that can be solved on the Leap hybrid solvers. The
general approach is based on that outlined by Lucas [2], which describes
formulation as a binary quadratic model. In Lucas's formulation, there are
N*N binary variables x_{v,i} (N denotes that number of nodes in each graph,
which must be the same for there to be an isomorphism) that represent whether a
vertex in the first graph gets mapped to a vertex in the second graph.
The objective function is expressed as two components, H_A and H_B
(Eqs. (71) and (72) in [2]). The first component, H_A, is used to enforce the
constraint that each vertex in each of the two graphs is selected exactly once:
We are able to simplify this equation by taking advantage of the discrete
quadratic model representation. Instead of using N*N binary variables, we use
N discrete variables, each having N cases. We let each discrete variable
represent a node in the first graph, and the N cases represent nodes in the
second graph. This way, the constraint of choosing each node in the first graph
once is implicitly enforced, and only the first of the two terms in the original
H_A equation is needed.
The second component, H_B (Eq. (72)), uses interaction terms to penalize
settings that select an edge in the first graph that is not in the second graph,
or vice versa:
The interaction coefficients associated with H_B are defined in the code using
two double-loops. Each double-loop includes an outer loop over the edges of one
of the two graphs, along with an inner loop over all possible node combinations,
so that penalty coefficients can be added for all combinations that are invalid.
The discrete quadratic model is then solved using the LeapHybridDQMSampler. If the two graphs are isomorphic, then the ground state energy is zero.
To check for circuit equivalence, we check two conditions: first, there must be an isomorphism between the two graphs. This can be determined based on the energy values found in the DQM solution. Second, for each isomorphism, we check that the corresponding circuit components are compatible. For the examples here, we simply check for compatibility of transistors (nMOS cannot be swapped with pMOS).
Some further simplifications to the formulation are possible, as discussed in Ref. [3]. For example, only nodes with the same degree in each graph are eligible to be matched. In the DQM formulation, this could be achieved by reducing the number of cases for each discrete variable so that only cases corresponding to nodes with an equal degree are included. This has the potential to significantly reduce the problem size, at the expense of additional bookkeeping to track the target nodes being represented by each discrete variable case.
[1] Johnson, DS. The NP-completeness column. ACM Transactions on Algorithms, 2005, 1-160. doi: 10.1145/1077464.1077476.
[2] Lucas, A. Ising formulations of many NP problems. Frontiers in Physics, 2014. doi: 10.3389/fphy.2014.00005.
[3] Zick, M., Shehab, O., and French, M. Experimental quantum annealing: case study involving the graph isomorphism problem. Scientific Reports 5, 2015. doi: 10.1038/srep11168.
Released under the Apache License 2.0. See LICENSE file.