This package contains tools for estimating haplotype (or allele list) frequencies in a population using measurements of unphased genotype data, that is, phenotypes.
In layman terms, a phenotype is defined as an observation of two-allele sets over multiple gene loci:
Aa ––––––– Bb ––––––– Cc
| | |
locus 1 locus 2 locus 3
Note that the above datum doesn't reveal what are the exact haplotype (allele sequence) pair behind the phenotype. Possible parent haplotype pairs that could result into the above phenotype are given by
(ABC, abc), (aBC, Abc), (AbC, aBc), (abC, ABc), ...
In other words, the mapping that maps a haplotype pair to a phenotype is defined by the example
(Abc, aBC) => (Aa, Bb, Cc)
and so on. Note that each item in the phenotype is a set of two alleles where the order doesn't matter.
Problem: Suppose that we have a set of phenotype observations from a large population of N individuals. For each individual phenotype we would like to estimate what are the most probable haplotype pair that resulted into the phenotype. The main ingredient of solution is the estimation of individual haplotype frequencies in the population
The package is found in PyPi.
pip install haplopyAlternatively, install development version manually using Pip:
git clone https://github.com/malmgrek/haplopy.git
pip install -r requirements
pip install -e .To check if the development version installed correctly, run tests with
pytest -v Simulate dataset using a prescribed haplotype probabilities and a multinomial distribution model.
import haplopy as hp
proba_haplotypes = {
("A", "B", "C"): 0.34,
("a", "B", "c"): 0.20,
("a", "B", "C"): 0.13,
("a", "b", "c"): 0.23,
("A", "b", "C"): 0.10
}
phenotypes = hp.multinomial.Model(proba_haplotypes).random(100)
fig = hp.plot.plot_haplotypes(proba_haplotypes)
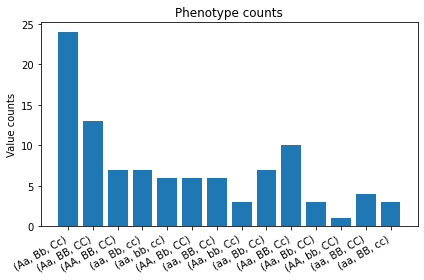
fig = hp.plot.plot_phenotypes(phenotypes)Pretend that we don't know the underlying haplotype distribution and let's try to estimate it.
model = hp.multinomial.Model().fit(phenotypes)
fig = hp.plot.plot_haplotypes(
model.proba_haplotypes,
thres=1.0e-6 # Hide probabilities smaller than this
)Use an existing model to calculate the probabilities (conditional to given the phenotype) of different diplotype representations of a given phenotype.
import haplopy as hp
model = hp.multinomial.Model({
("A", "B"): 0.4,
("A", "b"): 0.3,
("a", "B"): 0.2,
("a", "b"): 0.1
})
# A complete phenotype observation
model.calculate_proba_diplotypes(("Aa", "Bb"))
# {(('A', 'B'), ('a', 'b')): 0.4, (('A', 'b'), ('a', 'B')): 0.6}
# A phenotype with some missing SNPs
model.calculate_proba_diplotypes(("A.", ".."))
# {(('A', 'B'), ('A', 'B')): 0.17582417582417584,
# (('A', 'B'), ('A', 'b')): 0.2637362637362637,
# (('A', 'B'), ('a', 'B')): 0.17582417582417584,
# (('A', 'B'), ('a', 'b')): 0.08791208791208792,
# (('A', 'b'), ('A', 'b')): 0.09890109890109888,
# (('A', 'b'), ('a', 'B')): 0.13186813186813184,
# (('A', 'b'), ('a', 'b')): 0.06593406593406592}In particular, phenotype phasing also enables computing the probabilities of different admissible phenotypes as well as imputation of missing data:
model.calculate_proba_phenotypes(("A.", ".."))
# {('AA', 'BB'): 0.17582417582417584,
# ('AA', 'Bb'): 0.2637362637362637,
# ('Aa', 'BB'): 0.17582417582417584,
# ('Aa', 'Bb'): 0.21978021978021978,
# ('AA', 'bb'): 0.09890109890109888,
# ('Aa', 'bb'): 0.06593406593406592}
# Imputes with the most probable one
model.impute(("A.", ".."))
# ("AA", "Bb")