StanDDM

What is this package?

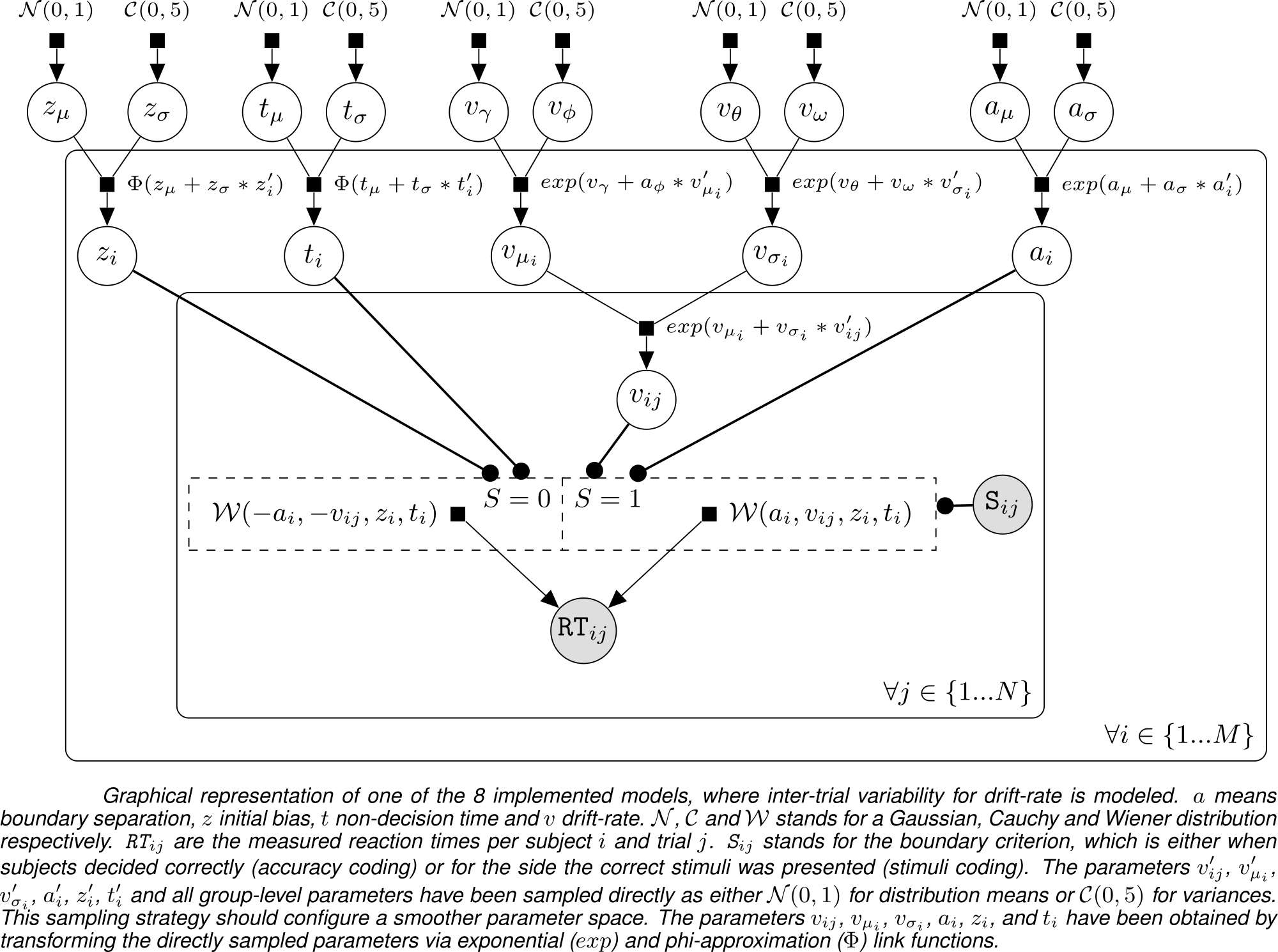
This R package implements a framework for fitting (Perceptual) Decision-Making Data with Bayesian Multi-Level Drift Diffusion Models. To this end, the package contains a collection of several Drift Diffusion Models, implemented in the probabilistic programming language Stan (Carpenter et al. 2017). It has been inspired by other packages, like "hBayesDM" (Ahn, Haines, and Zhang 2016) and "HDDM" (Wiecki, Sofer, and Frank 2013), but features its own take on model implementation, specifically on the trial-level. The multi-level Bayesian models are based on the work of (Vandekerckhove, Tuerlinckx, and Lee 2008). The general parameter-structure can be seen in the following directed acyclical graph:

A set of convenience functions for data simulation, model comparison and plotting are also supplied. The aim was to write and test "non-centered" parametrizations (Betancourt and Girolami 2015) of Multi-Level Bayesian models which incorporate inter-trial variabilities and are able to process different amounts of data per subject. The packages' fitting procedure can be also run on servers or clusters. Lastly, it also includes a automated parameter recovery for model testing without experimental data.

Errata: The negative signs on a and v on the lower threshold (when it is 0) intend to singify the direction of drift, not the actual sign of the value of the parameter. In hindsight, a poor choice.

Installation

devtools::install_github('https://github.com/mar-wir/StanDDM.git', ref = 'master')

Un-install

remove.packages('StanDDM')

Required Packages

StanDDM does not interface with the Stan library internally (for this to work, use the package 'rstantools' to create a package skeleton with the correct interfaces, I did learn of this too late... ¯|(ツ)|¯). Because of this, the Stan library has to be installed and loaded seperately. See here for more information: https://mc-stan.org/users/interfaces/rstan. The recommended packages to load are:

library(StanDDM) # This package
library(tidyverse) # For dplyr functionalities and everything tidy
library(magrittr) # For piping/streaming
library(rstan) # Stan framework

How to Fit a Model

Data Format:

The data required to fit a model with this package has following structure:

Subject-ID (Str.)	Reaction Times (sec.)	Diffusion Criterion	Answered correctly?
Subject1	1.53	1	1
Subject1	0.8	0	1
Subject1	1.2	1	0
...	...	...	...

The required columns and names are:

Subject-ID: suj
Reaction-Times (in seconds): rt
Diffusion Criterion: crit
Accuracy (trial answered correctly or not): cor

It is possible to fit the models according to a "stimuli-fitting" schema. This means that the decision-making data will be segregated according to which stimuli has been presented in a given trial. If stimuli-fitting is desired, then the variable crit needs to identify each stimuli.

If "Accuracy-fitting" is desired, then the data needs to be segregated according to the accuracy. In this case, the variables cor and crit need to be identical.

Note that each experimental condition has to be fit independently. You might have to filter your data before continuing, for example: data %<>% filter(group == "patient").

StanDDM comes with an example data-set. It can be accessed anytime:

dat <- StanDDM::example_data

print(head(dat))

# A tibble: 6 x 4
    suj    rt   cor  crit
  <int> <dbl> <int> <int>
1     1 0.590     1     1
2     1 0.449     0     0
3     1 0.537     1     1
4     1 0.286     0     0
5     1 0.339     1     1
6     1 0.474     1     1

Model Fit

dat <- StanDDM::example_data # Or alternatively, use your own, experimental data.

dat <- experimental_data_processing(dat) # Data requires to be formatted for fitting

StanDDM(data = dat, simulation = FALSE , include_models = c('Pure', 'st'))

The function StanDDM above will use the data dat to fit 2 models: First, the "Pure" DDM, also featured in the "hBayesDM" package, with no inter-trial variabilities. The second model, features inter-trial variability for the parameter "non-decision time". StanDDM features a total of 8 models and custom models can be included. See below for more details.

NOTE: Depending on your computer and the size of the data set and model choice, compilation and posterior exploration can take a long time and/or clog your memory. Save all work before starting any fitting procedures.

The StanDDM function saves the resulting stanfit objects in a folder inside the working directory, named after each model, in addition to diagnostic plots and a *csv file with the extracted parameters for each subject.

Include Custom Models

Custom models can also be added if they have the same form has the included model-functions. A template can be opened with the following command:

StanDDM::show_template() # Displays a template of a model-function to adapt.

Custom built models can be included by loading them into the workspace (they cannot have the same names as the models already included). Check the 'StanDDM' function documentation to see which strings are recognized. As an example, a custom model function has the name of Custom_regressionDDM. When loaded, they can be included as following:

StanDDM(data = dat, simulation = FALSE , include_models = c('Custom_regressionDDM'))

Should a string which cannot be recognized, be included in the 'include_models' argument, the package first checks if the function cannot be executed with its corresponding arguments. Only if this attempt fails, the 'StanDDM' function breaks.

Run Fitting procedure on Servers/Clusters

Because of the computational intensity of the included models, it is advisable to run them on an external machine. On a unix server, a R script called "run_models.r" for example, containing the below code has to be provided:

library(StanDDM) # This package
library(tidyverse) # For dplyr functionalities and everything tidy
library(magrittr) # For piping/streaming
library(rstan) # Stan framework

load('some_data.Rdata') #load experimental data with name 'some_data'

dat <- experimental_data_processing(some_data)

StanDDM(data = dat, simulation = FALSE , include_models = c('Pure', 'sv_sz', 'sv'))

This can be executed in bash: nohup rscript run_models.r > output.txt &. It is imortant to stream the generated output of the fitting procedure to a log!

Decision-Making Data Simulation

Simulates and structures perceptual decision-making data.

# Create parameters for 10 subjects, including inter-trial variability of non-decison time ('st').
fparams <- makeFakeParams(nsub = 10, include = c('st'))

# Simulate 100 trials per subject.
sims <- StanDDM::simulDat(fparams, n = 100)
dat <- sims[[1]]$data

The previous two steps are sufficient to simulate data. If you want also to fit the simulated data set, then this third step is required:

# Add the column 'crit', which means that the fitting will be accuracy fitting
dat %<>% 
    mutate(crit = cor) %>% 
    select(-cond) %>% 
    as_tibble()

dat <- experimental_data_processing(dat) # Needs to be formatted correctly with this function

Data Fit Assessment

StanDDM provides several ways to check how well data has been fitted: plots for visual inspection, R^2 and RMSE. Those functions are used automatically during the fitting procedure, but can also be called seperately. In the below use-case, we have a set of extracted DDM parameters (from any package), and we want to simulate data from those parameters to compare the result with our experimental data. This is done as follows:

data <- experimental_data_processing(patients) # Our experimental data

#Loading Parameters---------------------
params <- read_csv("some_ddm_parameters.csv") # Need to have a column for each parameter
rownames(params) <- data$forsim$names #giving simulation names of subjects (important!!)

#Simulate Data---------------------
sims <- simulDat(params)
sims <- sims[[1]]

#Rename Vars for Convenience---------------------
experim_dat <- data$forsim$rawdat # After data formatting, needs to be extracted from list
simul_dat <- sims

#PLOT AND COMPARE---------------------
fit_quality(experim_dat, simul_dat) #calculate RMSE and R2
models_plots(experim_dat, simul_dat) #will create new folder with plots comparing data and simuls

Model Comparison

After having fit several models, StanDDM provides 3 measures to compare and rank them: lppd, WAIC and LOO-CV (see (Gelman, Hwang, and Vehtari 2014) for more info). Code from the "LOO" package (https://github.com/stan-dev/loo) has been adapted for this purpose. The function "model_judgement" ranks all included models and compares them via a plot and table. The downside of this operation is that all models have to be loaded in memory to be evaluated, which heavily taxes R/R-Studio. This can be fixed, if demanded. Here an example:

load(fit1.Rdata)
load(fit2.Rdata)

model_judgement(fit1, fit2, impute_inf = TRUE)

The function implements a workaround for log-exp underflow values. See the function documentation for more information.

Priors

Please reason about the priors that make most sense in your setting and adapt the models accordingly!

About

I developed StanDDM for my masters thesis in Human Machine Communication, Department of Artificial Intelligence (Rijksuniversiteit Groningen) as an external project at the Laboratory of Cognitive Neuroscience (École polytechnique fédérale de Lausanne). I would like to thank my supervisors: Nathan Faivre, Michael Pereira (LNCO) and Marieke Van Vugt (ALICE) for their support and guidance.

References

Ahn, Woo-Young, Nathaniel Haines, and Lei Zhang. 2016. “Revealing Neuro-Computational Mechanisms of Reinforcement Learning and Decision-Making with the hBayesDM Package.” bioRxiv. Cold Spring Harbor Laboratory. doi:10.1101/064287.

Betancourt, Michael, and Mark Girolami. 2015. “Hamiltonian Monte Carlo for Hierarchical Models.” Current Trends in Bayesian Methodology with Applications 79. CRC Press Boca Raton, FL: 30.

Carpenter, Bob, Andrew Gelman, Matthew D Hoffman, Daniel Lee, Ben Goodrich, Michael Betancourt, Marcus Brubaker, Jiqiang Guo, Peter Li, and Allen Riddell. 2017. “Stan: A Probabilistic Programming Language.” Journal of Statistical Software 76 (1). Columbia Univ., New York, NY (United States); Harvard Univ., Cambridge, MA ….

Gelman, Andrew, Jessica Hwang, and Aki Vehtari. 2014. “Understanding Predictive Information Criteria for Bayesian Models.” Statistics and Computing 24 (6). Springer: 997–1016.

Vandekerckhove, Joachim, Francis Tuerlinckx, and Michael D Lee. 2008. “A Bayesian Approach to Diffusion Process Models of Decision-Making.” In Proceedings of the 30th Annual Conference of the Cognitive Science Society, 1429–34. Washington, DC.

Wiecki, Thomas V, Imri Sofer, and Michael J Frank. 2013. “HDDM: Hierarchical Bayesian Estimation of the Drift-Diffusion Model in Python.” Frontiers in Neuroinformatics 7. Frontiers: 14.

A work by Marco Wirthlin

marco.wirthlin@gmail.com