Political Districting to Minimize County Splits

Python code for the paper "Political districting to minimize county splits" by Maral Shahmizad and Austin Buchanan. Also available on Optimization-Online. Slides are also available.

We consider a stylized redistricting problem. The task is to divide a state into $k$ contiguous districts each having a population between $L$ and $U$ such that the number of county splits is minimum.

Tables near the end of the paper show the minimum number of splits versus the enacted splits for each state and district type (congressional, state senate, state house).

Approach

Our overall approach has three steps:

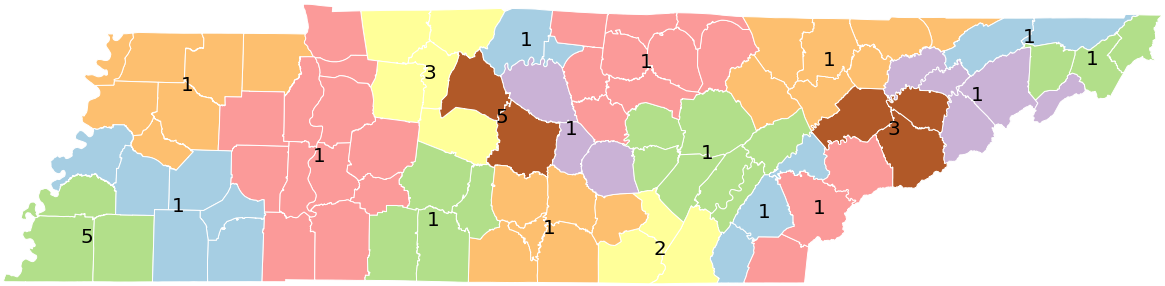
Cluster. Partition the counties into a maximum number of county clusters $(C_1, C_2, \dots, C_q)$ with associated cluster sizes $(k_1, k_2, \dots, k_q)$. If there are multiple such clusterings, pick one that is compact (i.e., few cut edges).
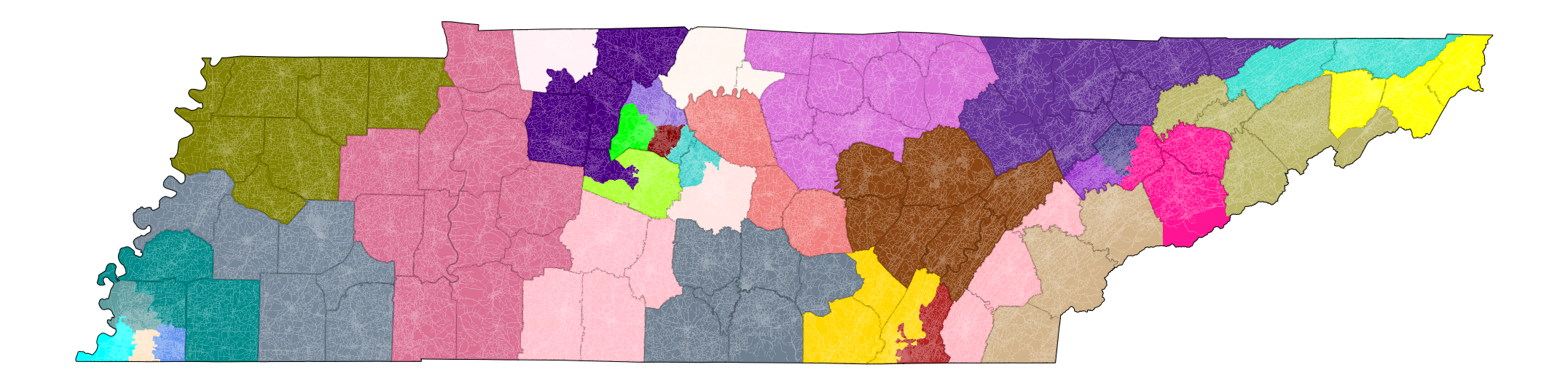
Sketch. For each cluster $C_j$, sketch a districting plan for it that has $k_j$ districts and $k_j-1$ county splits. A sketch indicates what proportion of each county is assigned to each district.
Detail. For each cluster $C_j$, find a detailed districting plan that abides by the sketch's support. That is, a tract (or block) is permitted in district $j$ only if its county is (partially) assigned to district $j$ in the sketch.

We solve each step using integer programming techniques. If the Cluster step is successful, then weak split duality implies that at least $k-q$ county splits are required (Theorem 1 of our paper, cf. Theorem 2 of Carter et al.). If the Sketch and Detail steps are successful, then we obtain a districting plan with $k-q$ splits. So, if all three steps are successful, we conclude that $k-q$ is the minimum number of county splits.

This is illustrated for the Tennessee's $k=33$ State Senate districts below. First, the Cluster step partitions Tennessee's $95$ counties into a maximum number of county clusters; there are $20$ clusters. By weak split duality, the minimum number of county splits is at least $33 - 20 = 13$. Second, the Sketch step determines what proportion of each county is assigned to each district (see pie charts), so that clusters of size $k'$ are carved up using $k'-1$ county splits. Third, the Detail step takes the district sketches and finds a detailed districting plan with $13$ splits. So, we have bounded the minimum number of splits between $13$ and $13$, so $13$ is optimal.

Cluster and Detail Results

We solve the minimum county splits problem for all congressional, state senate, and state house instances across the USA. For each instance, we identify the maximum number of county clusters (which gives a lower bound on the number of county splits), then we find a districting plan with the same number of splits, thus proving optimality in terms of splits. All experiments use the P.L. 94-171 data from the 2020 Census. Note that some states adjust their census data when creating their districting plans. We impose a 1% (+/-0.5%) deviation for congressional instances and a 10% (+/-5%) deviation for legislative instances.

We do not provide results for Hawaii given that it is a collection of islands, and contiguity is far from attainable.

We do not claim that the computer-generated maps from our experiments are "good" or that they should be enacted in practice. They do not consider the Voting Rights Act (VRA) or any laws that vary by state. However, as suggested Carter et al., it is possible for map drawers to use the maximum county clusterings as starting points and incorporate the VRA, state-specific laws, or other criteria in the Sketch and Detail steps. To achieve a minimum number of county splits, all that is required is to limit each cluster to $k'-1$ county splits, where $k'$ is the cluster's size.

State

Congress

Senate

House

maralshahmizad/Political-Districting-to-Minimize-County-Splits

Political Districting to Minimize County Splits

Approach

Cluster and Detail Results