The py_vollib_vectorized package makes pricing thousands of option contracts and calculating greeks fast and effortless.
It is built on top of the py_vollib library.
Upon import, it will automatically patch the corresponding py_vollib functions so as to support vectorization.
Inputs can then be passed as floats, tuples, lists, numpy.array, or pandas.Series.
Automatic broadcasting is performed on the inputs.
On top of vectorization, modifications to py_vollib include additional numba speedups; as such, numba is required.
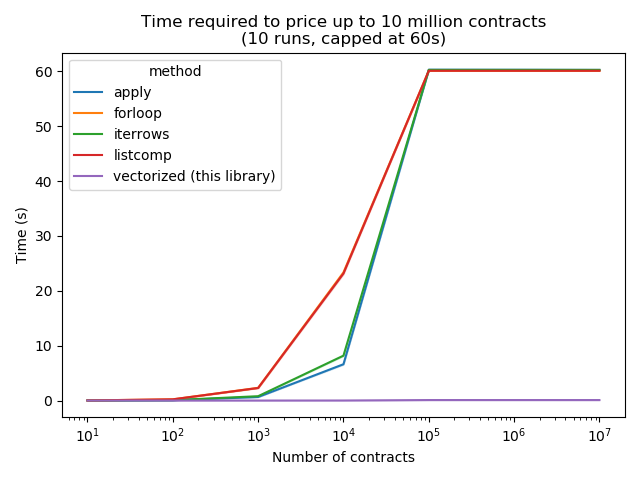
These speedups make py_vollib_vectorized the fastest library for pricing option contracts.
See the documentation for more details.
pip install py_vollib_vectorized
- Written for Python 3.5+
- Requires py_vollib, numba, numpy, pandas, scipy
The library can be used in two ways.
Upon import, it monkey-patches (i.e. replaces) the corresponding functions in py_vollib.
As a more versatile alternative, users that would prefer to work with a dedicated option pricing API can make use of the utility functions provided by the library.
# The usual py_vollib syntax
import numpy as np
import pandas as pd
import py_vollib.black_scholes
flag = 'c' # 'c' for call, 'p' for put
S = 100 # Underlying asset price
K = 90 # Strike
t = 0.5 # (Annualized) time-to-expiration
r = 0.01 # Interest free rate
iv = 0.2 # Implied Volatility
option_price = py_vollib.black_scholes.black_scholes(flag, S, K, t, r, iv) # 12.111581435
# This library keeps the same syntax, but you can pass as input any iterable of values.
# This includes list, tuple, numpy.array, pd.Series, pd.DataFrame (with only a single column).
# Note that you must pass a value for each contract as *no broadcasting* is done on the inputs.
# Patch the original py_vollib library by importing py_vollib_vectorized
import py_vollib_vectorized # The same functions now accept vectors as input!
# Note that the input arguments are broadcasted.
# You can specify ints, floats, tuples, lists, numpy arrays or Series.
flag = ['c', 'p'] # 'c' for call, 'p' for put
S = (100, 100) # Underlying asset prices
K = [90] # Strikes
t = pd.Series([0.5, 0.6]) # (Annualized) times-to-expiration
r = np.array([0.01]) # Interest free rates
iv = 0.2 # Implied Volatilities
option_price = py_vollib.black_scholes.black_scholes(flag, S, K, t, r, iv, return_as='array')
# array([12.11158143, 2.02418536])We also define other utility functions to get all contract prices, implied volatilities, and greeks in a single call.
import pandas as pd
from py_vollib_vectorized import price_dataframe, get_all_greeks
# Using the data above, we can calculate all contracts greeks in a single call
greeks = get_all_greeks(flag, S, K, t, r, iv, model='black_scholes', return_as='dict')
# {'delta': array([ 0.80263679, -0.21293214]),
# 'gamma': array([0.0196385, 0.01875498]),
# 'theta': array([-0.01263557, -0.00964498]),
# 'rho': array([0.34073321, -0.13994668]),
# 'vega': array([0.19626478, 0.22493816])}
# We can also price a dataframe easily by specifying a dataframe and the corresponding columns
df = pd.DataFrame()
df['Flag'] = ['c', 'p']
df['S'] = 95
df['K'] = [100, 90]
df['T'] = 0.2
df['R'] = 0.2
df['IV'] = 0.2
result = price_dataframe(df, flag_col='Flag', underlying_price_col='S', strike_col='K', annualized_tte_col='T',
riskfree_rate_col='R', sigma_col='IV', model='black_scholes', inplace=False)
# Price delta gamma theta rho vega
# 2.895588 0.467506 0.046795 -0.045900 0.083035 0.168926
# 0.611094 -0.136447 0.025739 -0.005335 -0.027151 0.092838See the documentation for more details.
Compared to looping through contracts or to using built-in pandas functionality, this library is very memory efficient and scales fast and well to a large number of contracts.
This library optimizes the py_vollib codebase, itself built upon Peter Jäckel's Let's be rational methodology.