Verification of PeleC uses MASA, an auto-differentiation MMS tool, to implement the Method of Manufactured Solutions into PeleC.
There L_2 error norm for a quantity s is defined as
e_s = \sqrt{ \frac{\sum_{i=1}^{N_e} \int_{V_i} (s^h-s^*)^2 \mathrm{d}V}{\sum_{i=1}^{N_e} \|V_i\|}}
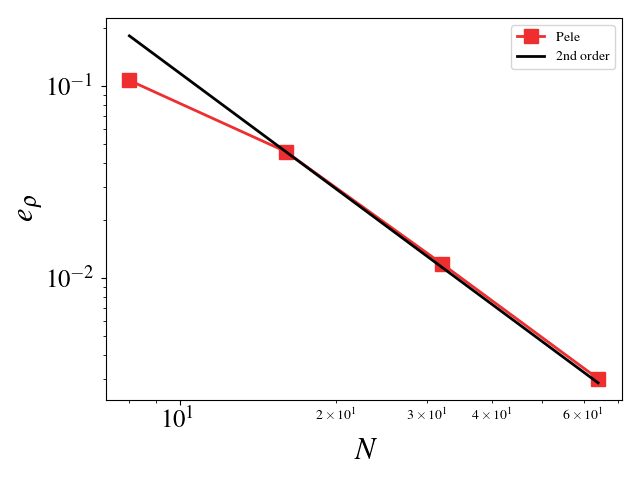
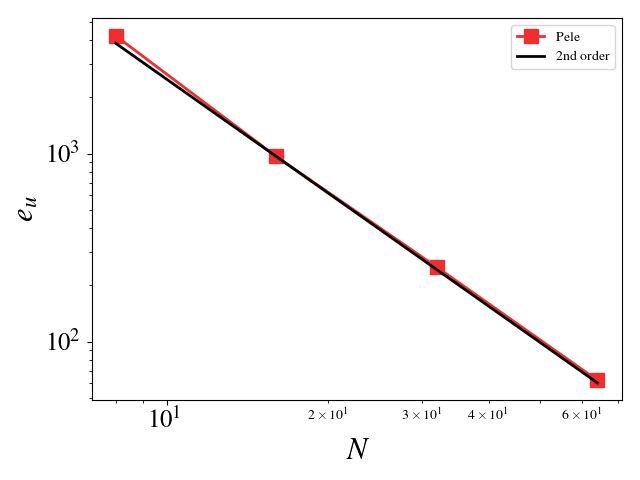
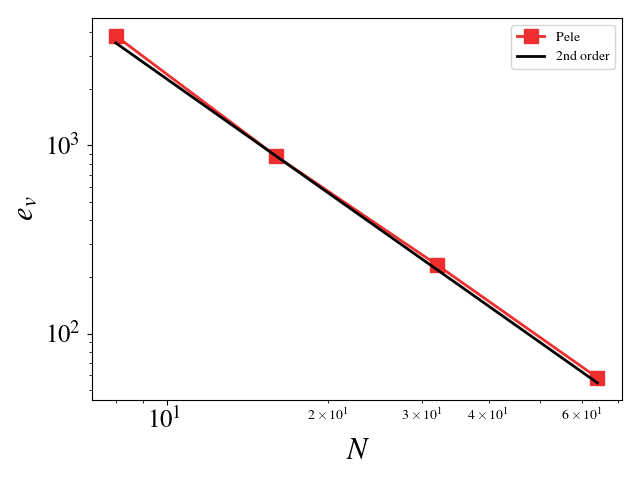
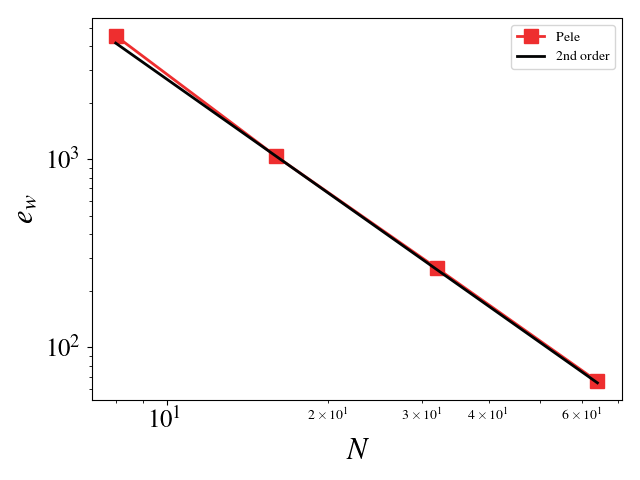
where s^h is the numerical solution, s^* is the exact solution, and N_e is the number of elements. N, used below, is the number of element on a side of the cube (N_e = N^3).
The user must first build and install MASA. The MASA install location must be specified in the GNUMakefile of the MMS problem setup.
Make sure you change the install paths to match what you want it to be.
- Get Metaphysicl
./bootstrap(on Peregrine, dospack load autoconffirst)./configure --prefix=${HOME}/combustion/install/MetaPhysicLmakemake install
- Get MASA
./boostrap(on Peregrine, dospack load autoconffirst`)./configure --enable-fortran-interfaces METAPHYSICL_DIR=${HOME}/combustion/install/MetaPhysicL --prefix=${HOME}/combustion/install/MASA --enable-python-interfacesmakemake checkmake install
MASA must be linked to when building Pele. The user must have defined the MASA_HOME variable to point to the install location of MASA. The user can specify the MASA solution to be used in the input file (option: pc_masa_solution_name).
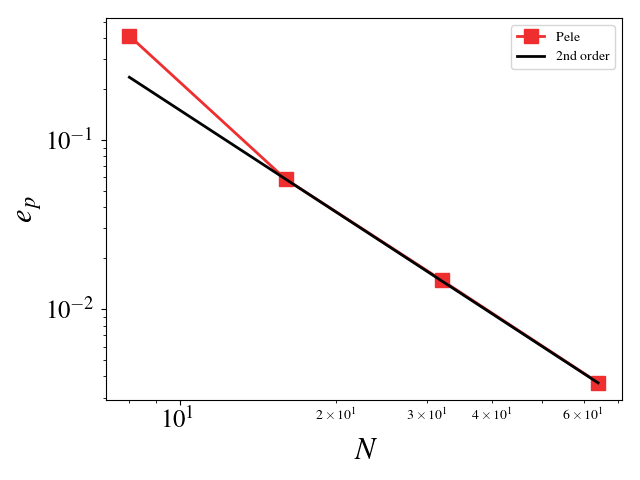
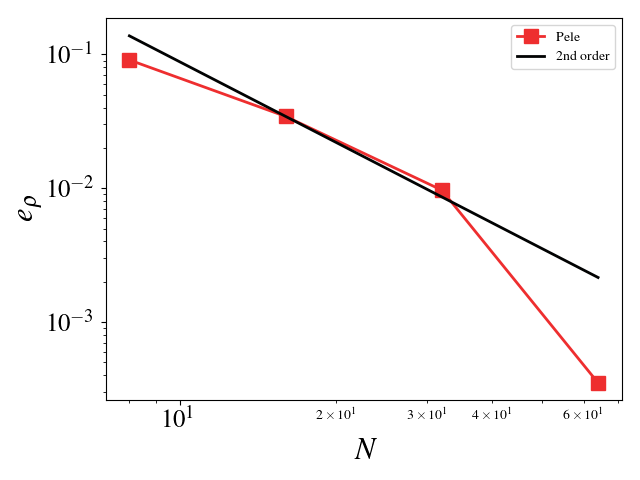
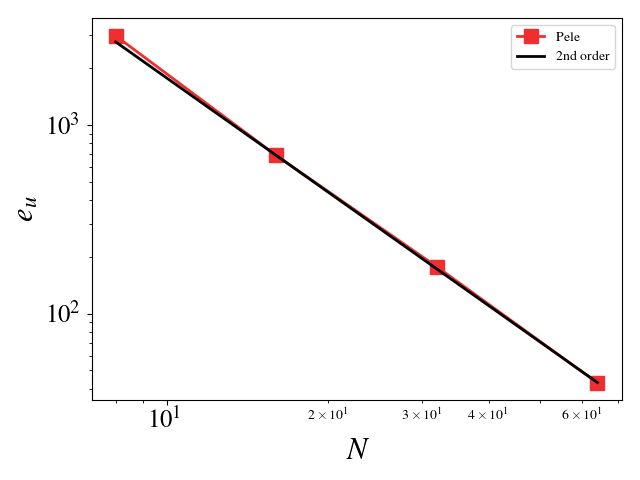
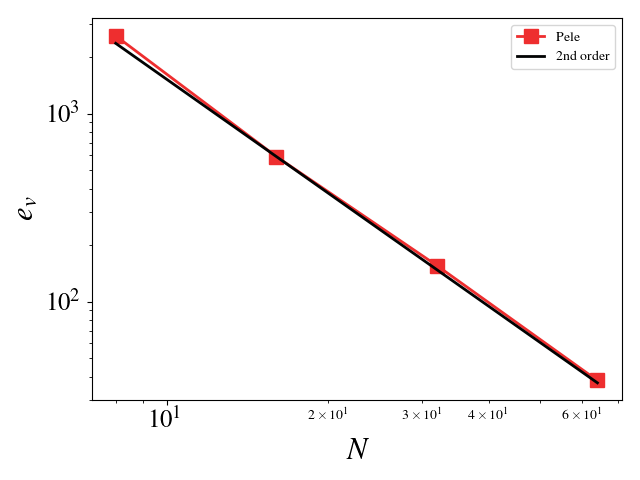
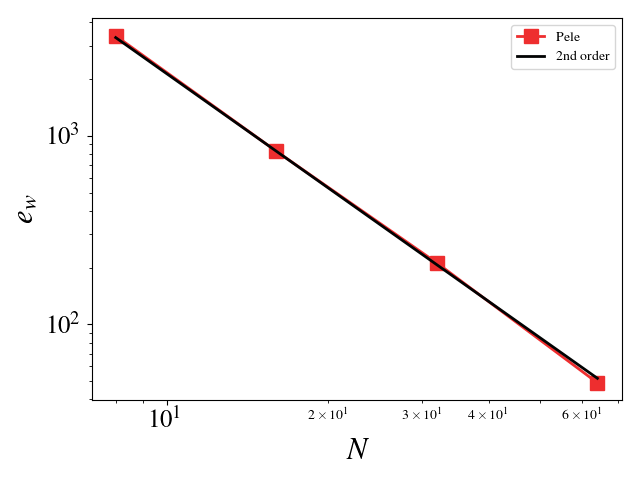
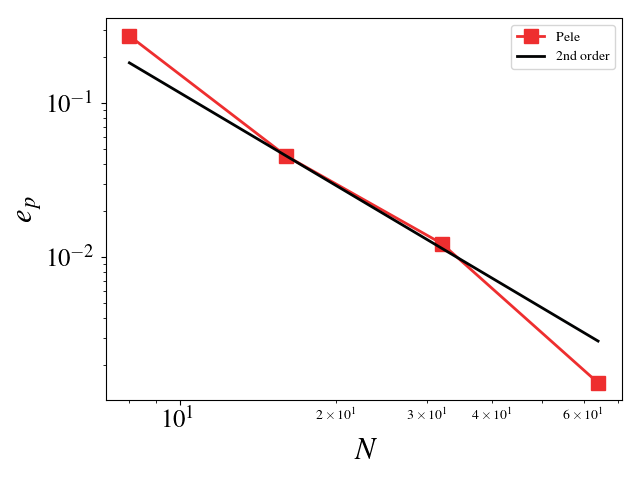
For these cases, the Reynolds, Mach, and Prandtl numbers were set to 1 to ensure that the different physics were equally important (viscosity, conductivity, and bulk viscosity are non-zero and determined by the appropriate non-dimensional number). The CFL condition was fixed to 0.1 to ensure that the predictor-corrector time stepping method found a solution to the system of equations. The initial solution was initialized to the exact solution. Periodic boundaries are imposed everywhere. A convergence study shows second order for Pele's treatment of the compressible Navier-Stokes equations.
Initial difficulties in getting the solution to reach steady state for the Euler equations (no diffusion) were overcome by incorporating diffusion effects and reducing the CFL number. Setting the Reynolds, Mach, and Prandtl to 1, and taking small time steps ensures that the pseudo-time integration (predictor/corrector) does not oscillate wildly and fail to find the steady-state solution. The iterative error was monitored and the final time (identical for all simulations) was chosen so that the iterative error was small, \mathcal{O}(10^{6}) smaller than the discretization error. The iterative error never reaches machine zero. This is most likely due to the way in which the predictor/correct pseudo-time integration uses time steps based on the wave speeds and viscosity and not adjusting the time step based on the Jacobian of the system. An actual steady-state solver (rather than a pseudo-time integration to steady state) would be more efficient and more robust at finding the steady state solution of the MMS system of equations. While this would test the spatial discretization scheme, an MMS simulation with a steady state solver would fail to test the temporal discretization scheme.
- Density L_2 error norm:
- Velocity (u, v, w) L_2 error norm:
- Pressure L_2 error norm:
This setup is similar to the previous one except for the fact that this test uses the AMR framework. There are two grid refinement levels: a coarse grid covering the entire domain and a fine grid on top of this one covering 50% of the domain. The grids are fixed in time, i.e. they do not adapt based on the solution value. This test ensures that the algorithms dealing with the grid interfaces, time integration of the different levels, and level synchronization preserve the second order accuracy of the code.
- Magnitude of velocity and mesh:
- Density L_2 error norm:
- Velocity (u, v, w) L_2 error norm:
- Pressure L_2 error norm: