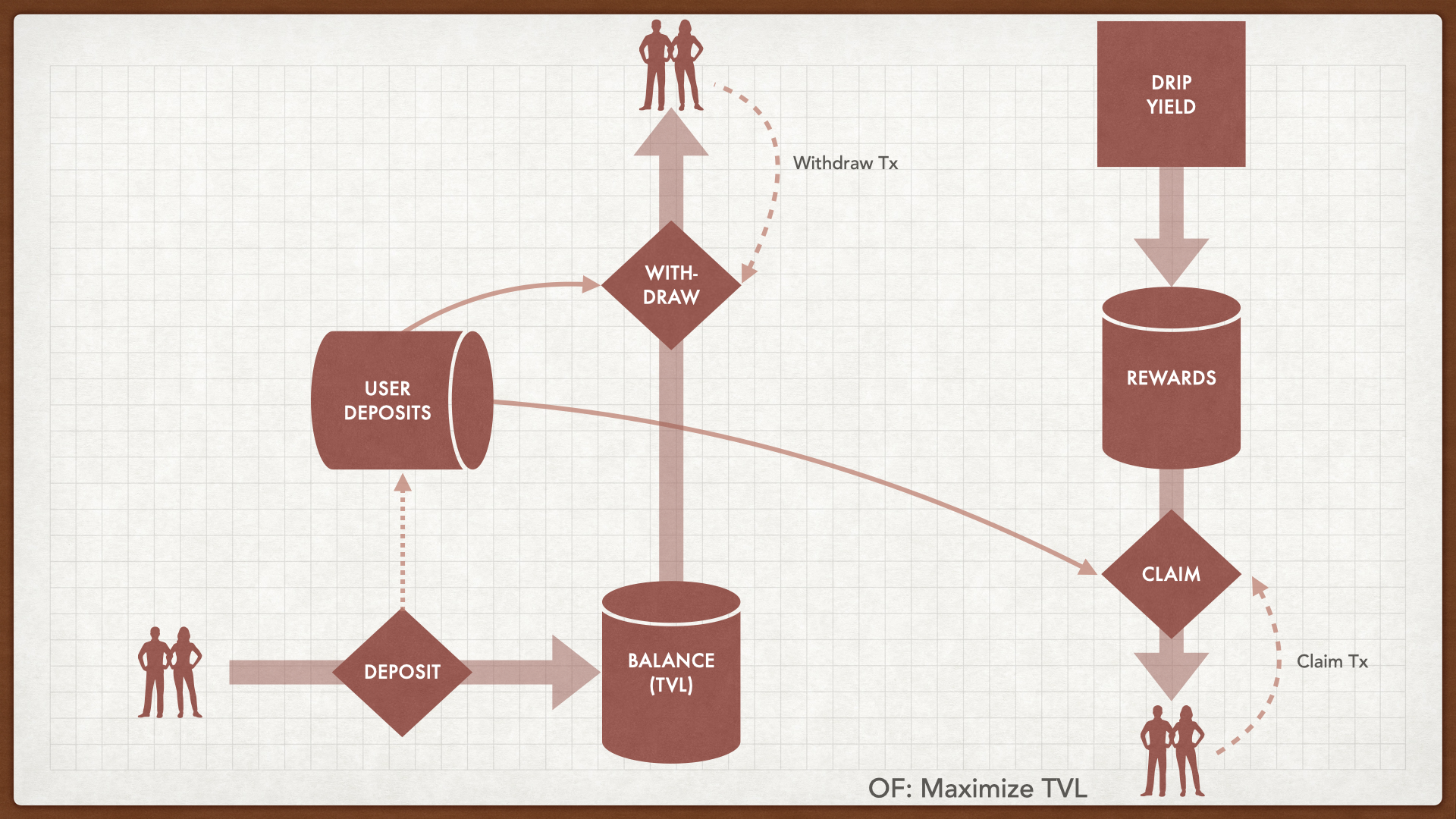
an educational example for the New Order founder bootcamp
This is a simple model of Vaults and Stakers earning Yield
Each Staker $i$ is an actor having a balance $b_i$ of tokens and the Staker can stake these tokens in vaults (described below). Each Staker has its own expectation of yield $x_i$.
$I$ is the set or collection of all Stakers such that $i \in I$
Each Vault $j$ maintains a deposit balance $s_{ij}$ for each Staker $i$.
Each Vault $j$ holds a total amount of stake $S_j$ deposited by all Staker $i$ such that $\sum s_{ij} = S_j$
Each Vault has an incoming reward stream $R_j$ that is distributed amongst Stakers each epoch or time step.
$J$ is the set or collection of all Vaults such that $j \in J$
TODO: define how rewards are accounted for in the model
When Staker $i$ deposits an amount of tokens $\Delta b_i$ into Vault $j$, state is updated as follows:
The updated amount of stake in $j$ is:
$S_j^+ = S_j+\Delta b_i$
The updated deposit balance of stake $j$ is holding for $i$ is:
$s_{ij}^+=s_{ij}+\Delta b_i$
The updated balance of the staker $i$ is:
$s_{ij}^+ = s_{ij} - \Delta b_i$
The maximum amount $i$ can deposit is:
$\Delta b_i\leq b_i$
When Staker $i$ withdraws an amount of tokens $\Delta s_{ij}$ from Vault $j$, state is updated as follows:
The updated amount of stake in $j$ is:
$S_j^+ = S_j-\Delta s_{ij}$
The updated deposit balance of stake $j$ is holding for $i$ is:
$s_{ij}^+=s_{ij}-\Delta s_{ij}$
The updated balance of the staker $i$ is:
$s_{ij}^+ = s_{ij} + \Delta s_{ij}$
The maximum amount $i$ can withdraw is:
$\Delta s_{ij}\leq s_{ij}$
TODO
Assumption: for the time being only consider one reward stream.
The reward at each time step $r_{ij}$ for each Staker $i$ from Vault $j$ is
$\forall i,\forall j: r_{ij} = \frac{s_{ij}}{S_j}* R_j$
TODO
Objective function:
$MAX \frac{S_j}{R_j}$
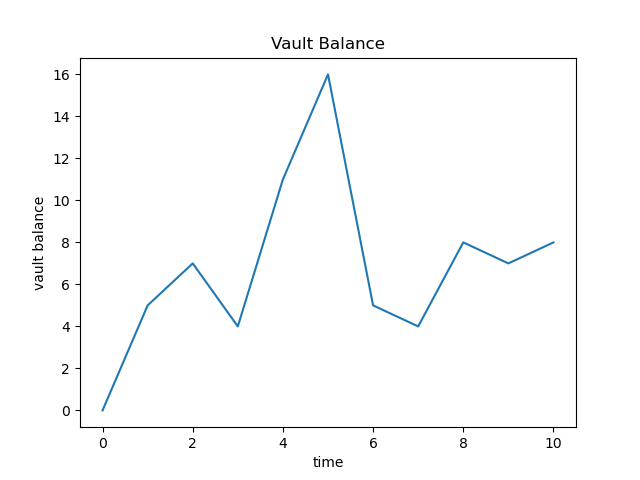
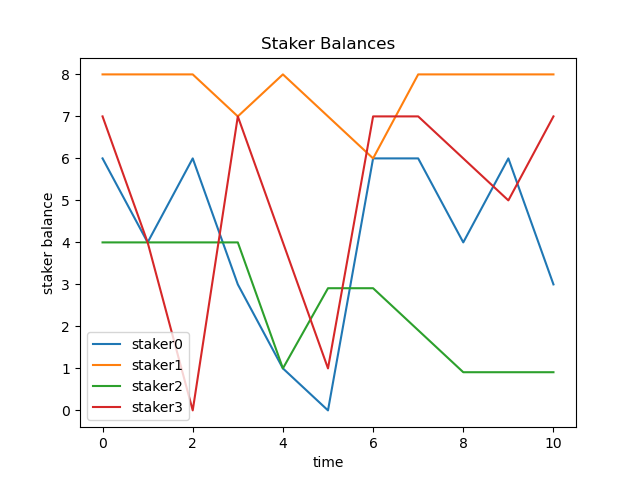
Results of one run with 1 vault, 4 stakers, and 10 timesteps