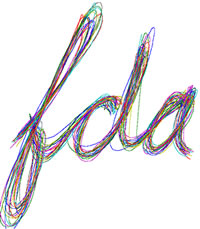This is the original code developed by Jim Ramsay for MATLAB. I first put it up on Github when the code no longer appeared to be available at http://www.psych.mcgill.ca/misc/fda/. I've been informed it is now there, but I think it might still be convenient to have it available on Github where it can be more easily found. This code is the version dating from 08/08/2017, the last available version I was able to obtain from the Wayback Machine internet archive, https://web.archive.org/web/20170713053602/http://www.psych.mcgill.ca/misc/fda/
I reproduce Ramsay's front page to his FDA site:
Functional data analysis, which lots of us like to call "FDA", is about the analysis of information on curves or functions. For example, these twenty traces of the writing of "fda" are curves in two ways: first, as static traces on the page that you see after the writing is finished, and second, as two sets functions of time, one for the horizontal "X" coordinate, and the other for the vertical "Y" coordinate.
FDA is a collection statistical techniques for answering questions like, "What are the main ways in which the curves vary from one writing to another?" In fact, most of the questions and problems associated with the usual multivariate data analyzed by statistical packages like SAS and SPSS have their functional counterparts.
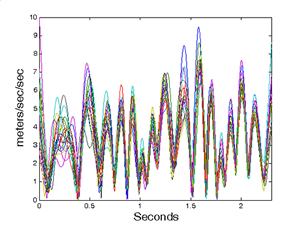
But what is unique about functional data is the possibility of also using information on the rates of change or derivatives of the curves. We use slopes, curvatures, and other characteristics made available because these curves are intrinsically smooth, and we can use this information in many useful ways. For example, our high school physics tells us that force = mass times acceleration, and that suggests that we look at the acceleration or second derivative of the pen's position as a function of time. What we see in the plot of the magnitudes of the acceleration vector is that acceleration hits nearly ten meters/second/second. That's a lot of energy! Equally remarkable is the stability of these acceleration records from one trial to the next. Also, note that where the acceleration magnitudes are near zero, both the X and Y accelerations must simultaneously be zero. The brain seems to know what it's doing!
Wikipedia: https://en.wikipedia.org/wiki/Functional_data_analysis
Ramsay & Silverman's book, "Functional Data Analysis". Essential reading if you want to get into FDA. There are usually second copies available.