Test program for adaptive time stepping in a gravitational NBody system
This is a simple N-Body gravitational direct solver. The aim is to experiment with particle ordering and methods to adapt the time step by factors of 2 for groups of particles in order to complete the work faster with similar total error. As seen below, the method can run a simulation 100x faster with no change in total system RMS error. This is because in these systems, the maximum errors are primarily encountered on a small, but rapidly-moving subset of particles.
With g++ installed, you can simply run:
make
./adapDt.bin -n=10000 -s=5
Generate and save a re-usable set of particles, find the "true" solution, and compare to it later:
./adapDt.bin -n=10000 -s=0 -o=initial.dat
./adapDt.bin -n=10000 -s=10 -i=initial.dat -true -o=truesoln.dat
./adapDt.bin -n=10000 -s=10 -i=initial.dat -c=truesoln.dat
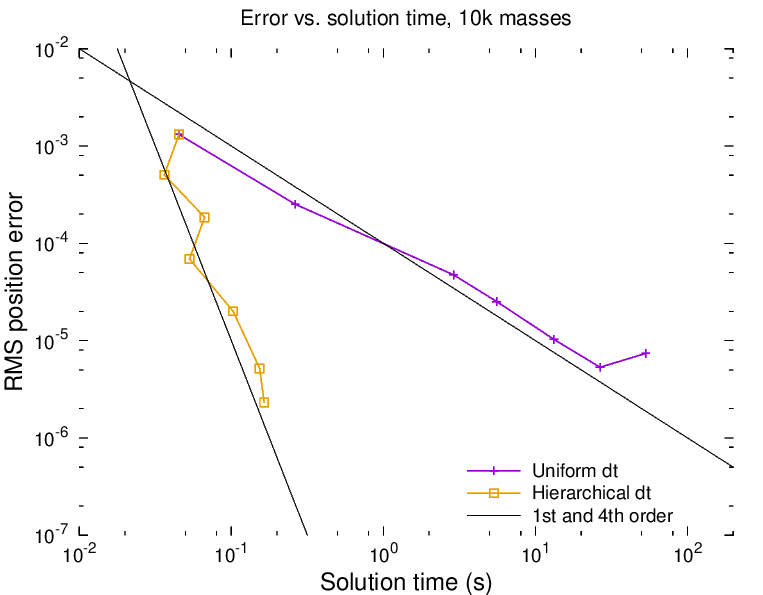
Above is a plot of the system RMS position error vs. total simulation time for an O(N^2) n-body simulation of 10,000 particles in gravitational motion using 1st order Euler (explicit) time stepping. The particles are clustered around the origin, and the particle masses distribution follows an inverse power law. The uniform Dt cases ran from 10 to 20,000 uniform time steps (dt=0.01 to 5.e-6). The Hierarchical Dt case used 10 time steps at the coarsest level, and the data points represent the case where the finest time step equals the coarse time step, and subsequent cases all allow the finest time step to be refined by two factors of 2 for each data point on the plot. The last data point on Hierarchical Dt case represents particles stepping at between 0.01 per step and 0.01 * 0.5^12 = 2.4e-6. For the Hierarchical case, the particles are first sorted by jerk magnitude, and then at each level, 50% of the particles with the highest initial jerk magnitude are flagged for time refinement. Thus, the simulation is not truly solution-adaptive; for that, the jerk would need to be evaluated at each time step and particles would be free to move toward more or less time-refinement to control error.
The key principle in this code is that of a hierarchy across N (particles) and time. A block in this hierarchy conists of "slow" particles, which will take one long time step, and "fast" particles, which will take two time steps across the same time interval. A simple particle system would keep these two sets of particles and march forward in time, at the two rates.
But to make the method hierarchical and really achieve substantial improvements in performance, one time step of the "fast" particles becomes another block, and is subsequently decomposed into "slow" and "fast" particles, with these fast-fast particles advancing using timesteps that are one fourth the duration of the top-level slow particles.
Because the error in forward advection systems scales with the time step size and the magnitude of the (order+1)-th derivative, we can use that value (calculated using Biot-Savart or estimated from previous steps) to determine the slow-fast split at each level in the hierarchy.
Currently, this code is for universal gravitation, so uses mass, position, and radius (for smoothing) to compute the accelerations. Thus, jerk magnitude (the 2-norm of the gradient of accleration) is the parameter used to separate particles into "slow" and "fast" varieties. The code uses 1st-order Euler time stepping for the velocity (and midpoint rule for the position), because otherwise we would need a more complicated multi-step or multi-stage integrator.
- Support higher-order forward integrators (Verlet or AB2 come to mind, but they must support variable time step lengths)
- At the very least, support a higher-order integrator when calculating the "true" solution - at least RK4 using uniform step sizes
- Make the slow-fast splits solution-adaptive (according to jerk magnitude)
- Be smarter about calculating error - move it into one of the structs
- Consider passing one std::span (c++20) instead of 3 separate values
- Keep the MPI version up-to-date
I don't get paid for writing or maintaining this, so if you find this tool useful or mention it in your writing, please please cite it by using the following BibTeX entry.
@Misc{adapDt2023,
author = {Mark J.~Stock},
title = {adapDt: Adaptive time stepping for NBody systems},
howpublished = {\url{https://github.com/markstock/adapDt}},
year = {2023}
}