The code repository of the paper:
Z.Wang and G.Xia, MuseBERT: Pre-training of Music Representation for Music Understanding and Controllable Generation, ISMIR 2021.
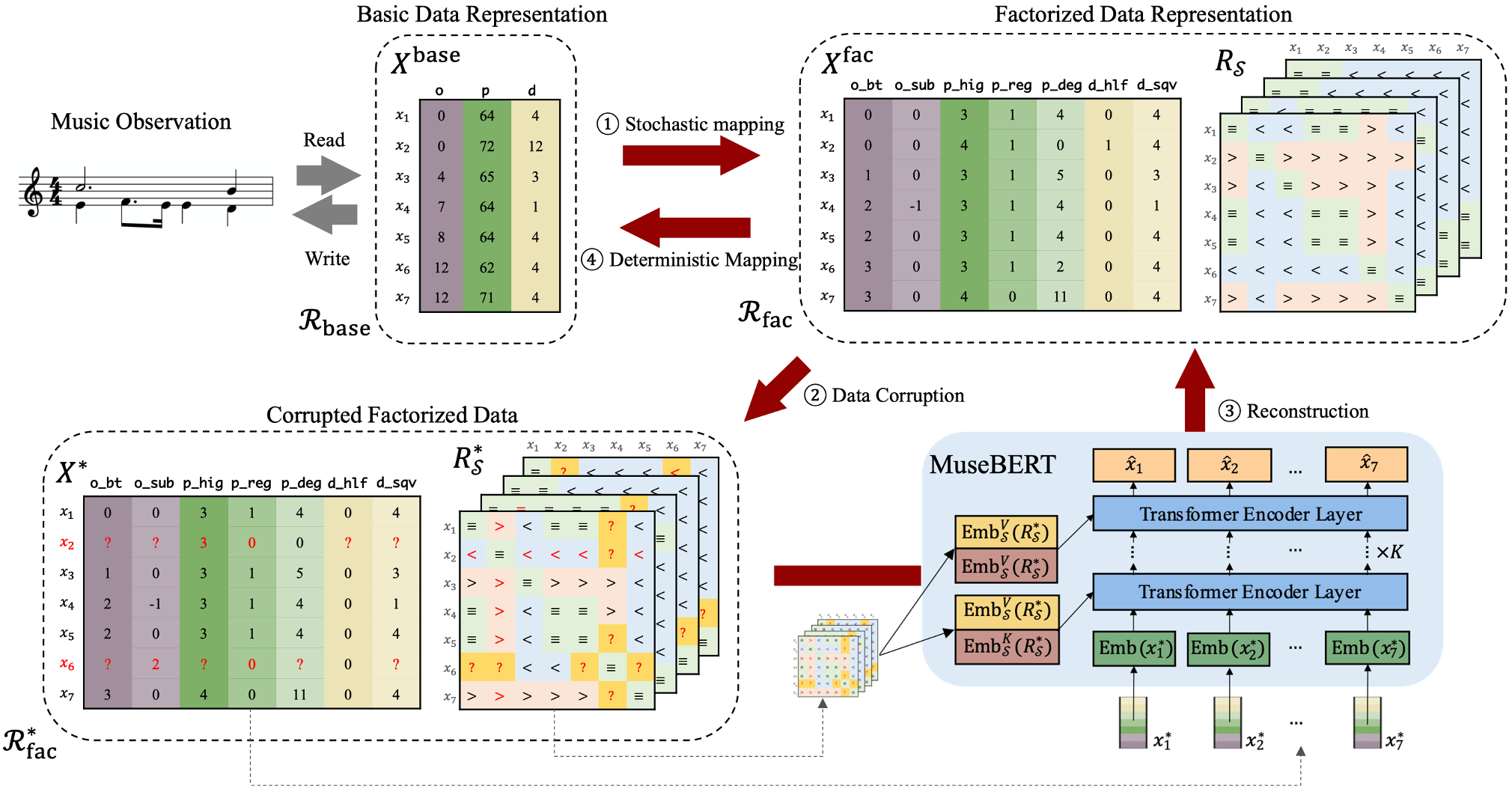
In this initial commit, we open source the core of MuseBERT: the entire workflow of MuseBERT. The workflow is used in both pre-training and fine-tuning. It contains four steps:
-
Stochastic mapping:
$X^\text{base}$ is a note matrix of size$(L, 3)$ consisting of$L$ notes and$3$ attributes of onset, pitch and duration. It is stochastically converted to more detailed note attributes$X^{\text{fac}}$ of size$(L, 7)$ , together with a stack of relation matrices$R_\mathcal{S}$ of size$(4, L, L)$ . - Data corruption: Data corruption is applied in BERT-like fashion where 1) note attributes are masked/replaced/kept at random. Relation matrices are recomputed (because there are replaced attributes) and masked at random.
-
Reconstruction: MuseBERT model is applied to reconstruct the input
$X^\text{fac}$ , where masked attributes are fed as model input and corrupted relations are fed as generalized relative positional encoding. -
Deterministic Mapping: the reconstructed factorized data is decoded back to
$X^\text{base}$ .
There are several implementation details worth-mentioning:
- MuseBERT does not use absolute positional encoding.
- In practice, data corruption over relation matrices are not recomputed. We first compute the relation matrices based on a replaced-only
$X^*$ (an intermediate product) and then apply mask corruption by generating a stack of symmetrical masks. - We propose novel Generalized Relative Positional Encoding introduced in eq. (10) & (11) of our paper. The direct implementation is not affordable in time complexity. We therefore implement GRPE in an effficient way:
- We uses distributive law to both eq. (10) & (11).
- Since the embedding of the same relation (e.g.,
$<$ ) will be used in many place, we compute it only once and avoid expanding relation matrices embedding into$(L, L, \text{emb_dim})$ .
- Loss is applied to corrupted tokens only. In our implementation, we compute the loss in the fashion where each segment (in a batch) is treated equally regardless of the different number of corrupted tokens. For example, bs=2,
$N_1$ sample in sample 1, and$N_2$ samples in sample 2, the weighting is:[0.5 / N_1]* N_1 + [0.5 / N_2] * N_2.
A brief introduction of what is in each file:
-
note_attribute_repr.py: converting between$X^\text{base}$ to$X^\text{fac}$ . -
note_attribute_corrupter.py: computing relation matrices and data corruption. -
transformer.py: implementatino of GRPE and a modified Transformer encoder. -
musebert_model.py: implementation of MuseBERT model. -
curriculum_preset: preset hyperparameters of MuseBERT workflow, model architecture and training. -
curricula.py: handling of hyperparameters for different presets for pre-training and different types of fine-tuning. -
dataset.py,utils.py,train.pyetc.
python train.py
As stated in our paper as well, we see our model as a powerful controllable music generator and analyzer. However, it is still in its perliminary stage. We plan to update the code including more downstream fine-tuning tasks, and a more complete illustration of the entire MuseBERT methodology.
The paper is written in a very rigorous manner with clear definition and theorem proving, which is very rare in music generation studies. Nevertheless, we believe this is a proper way to present our work in the sense that our model adds music control from the token-wise/lexeme level of music, and an isomorphism is made between a BERT problem and a way of generalized positional encoding, and between a BERT problem and a constraint solver.
Problems and discussion on this paper is welcome. Please contact me at ziyu.wang@nyu.edu.