- Non-negative tensor decomposition implementation for Common Lisp
- Update algorithm: Multiplicative Update (MU) for minimization of KL divergence
- Support sparse tensor only
ros install masatoi/cl-tensor-decomposition
(in-package :cltd)
;; Prepare sparse tensor
(defparameter X-shape '(2 3 4))
(defparameter number-of-non-zero-elements 3)
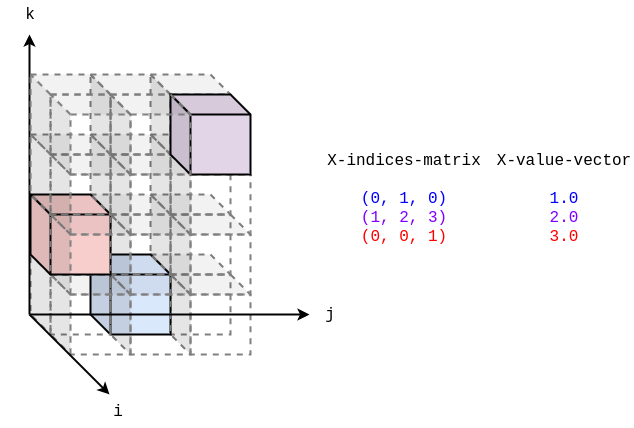
(defparameter X-indices-matrix
(make-array (list number-of-non-zero-elements
(length X-shape))
:element-type 'fixnum
:initial-contents '((0 1 0) ; The row corresponds a element of one datum
(1 2 3)
(0 0 1))))
(defparameter X-value-vector
(make-array number-of-non-zero-elements
:element-type 'single-float
:initial-contents '(1.0 2.0 3.0)))
;; Decomposition
(decomposition X-shape X-indices-matrix X-value-vector :n-cycle 10 :R 2 :verbose t)
#|
cycle: 1, kl-divergence: 9.594987
cycle: 2, kl-divergence: 8.59509
cycle: 3, kl-divergence: 5.7237873
cycle: 4, kl-divergence: 1.3804492
cycle: 5, kl-divergence: 0.94020593
cycle: 6, kl-divergence: 0.78665006
cycle: 7, kl-divergence: 0.74955434
cycle: 8, kl-divergence: 0.7494588
cycle: 9, kl-divergence: 0.74934554
cycle: 10, kl-divergence: 0.7493448
#(#2A((0.0 1.2894418) (0.73389024 0.0))
#2A((4.4436022e-24 1.333183) (6.0661177e-22 0.44439435) (1.7189547 0.0))
#2A((1.1754372e-39 0.4362844)
(2.2280646e-43 1.3088531)
(0.0 0.0)
(1.585384 0.0)))
|#A sparse tensor consists of pairs of non-zero values and indices.
- Multiple Data Analysis and Non-negative Matrix/Tensor Factorization [II. Finish] : Tensor Data Analysis and Applications http://www.kecl.ntt.co.jp/icl/ls/members/tatsushi/PDF/IEICE_vol99_no7_691-698.pdf