- Python 3.7 or newer
- NumPy
- Gaussian 09 or 16
- The path of the Gaussian must be set.
| Short | Long | Explanation |
|---|---|---|
| -a | --apta | Perform atomic pair transfer analysis. |
| -c | --cube | Generate cube files. |
| -g | --g09 | Use Gaussian 09. (default is Gaussian 16) |
| -h | --help | Show options description. |
| -l | --lumo | Perform atomic pair transfer analysis of LUMO. |
| -m | --matrix | Print MO coefficients, overlap matrix and Fock matrix. |
| -o | --output | Output csv file on the result of apta. |
| -r | --read | Read log files without executing Gaussian. |
| -x | --xyz | Convert xyz file to gjf file. |
| --napta N1 N2 | Perform atomic pair transfer analysis between different levels. N1 is the number of level in the first monomer. N2 is the number of level in the second monomer. | |
| --hetero N | Calculate the transfer integral of heterodimer. N is the number of atoms in the first monomer. | |
| --nlevel N | Calculate transfer integrals between different levels. N is the number of levels from HOMO-LUMO. N=0 gives all levels. | |
| --skip N... | Skip specified Gaussian calculation. If N is 1, skip 1st monomer calculation. If N is 2, skip 2nd monomer calculation. If N is 3, skip dimer calculation. |
First of all, create a gaussian input file as follows:
ex: xxx.gjf
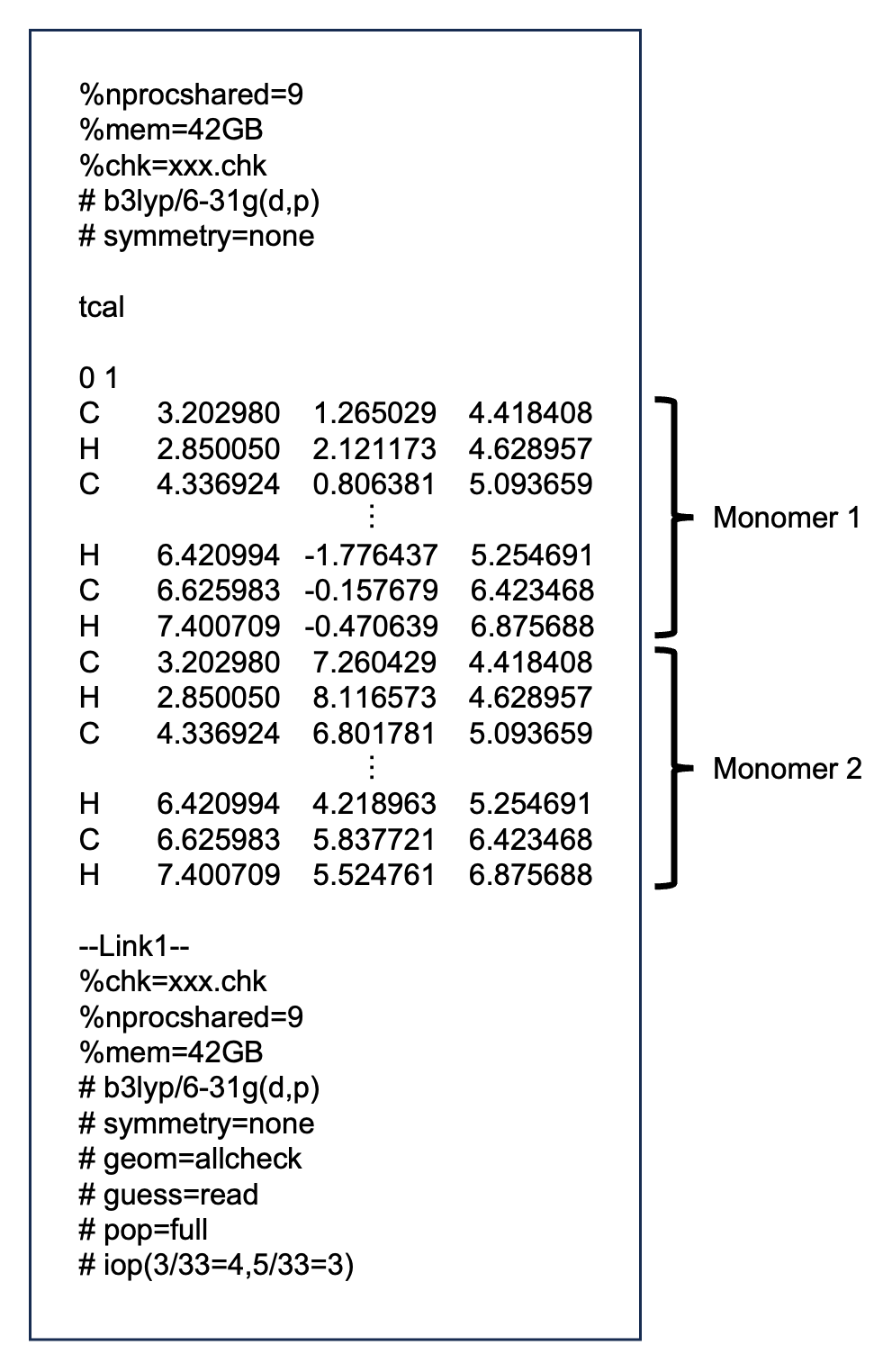
The xxx part is an arbitrary string.
pop=full: Required to output coefficients of basis functions, overlap matrix, and Fock matrix.
iop(3/33=4,5/33=3): Required to output coefficients of basis functions, overlap matrix, and Fock matrix.
- Open cif file in Mercury.
- Display the dimer you want to calculate.
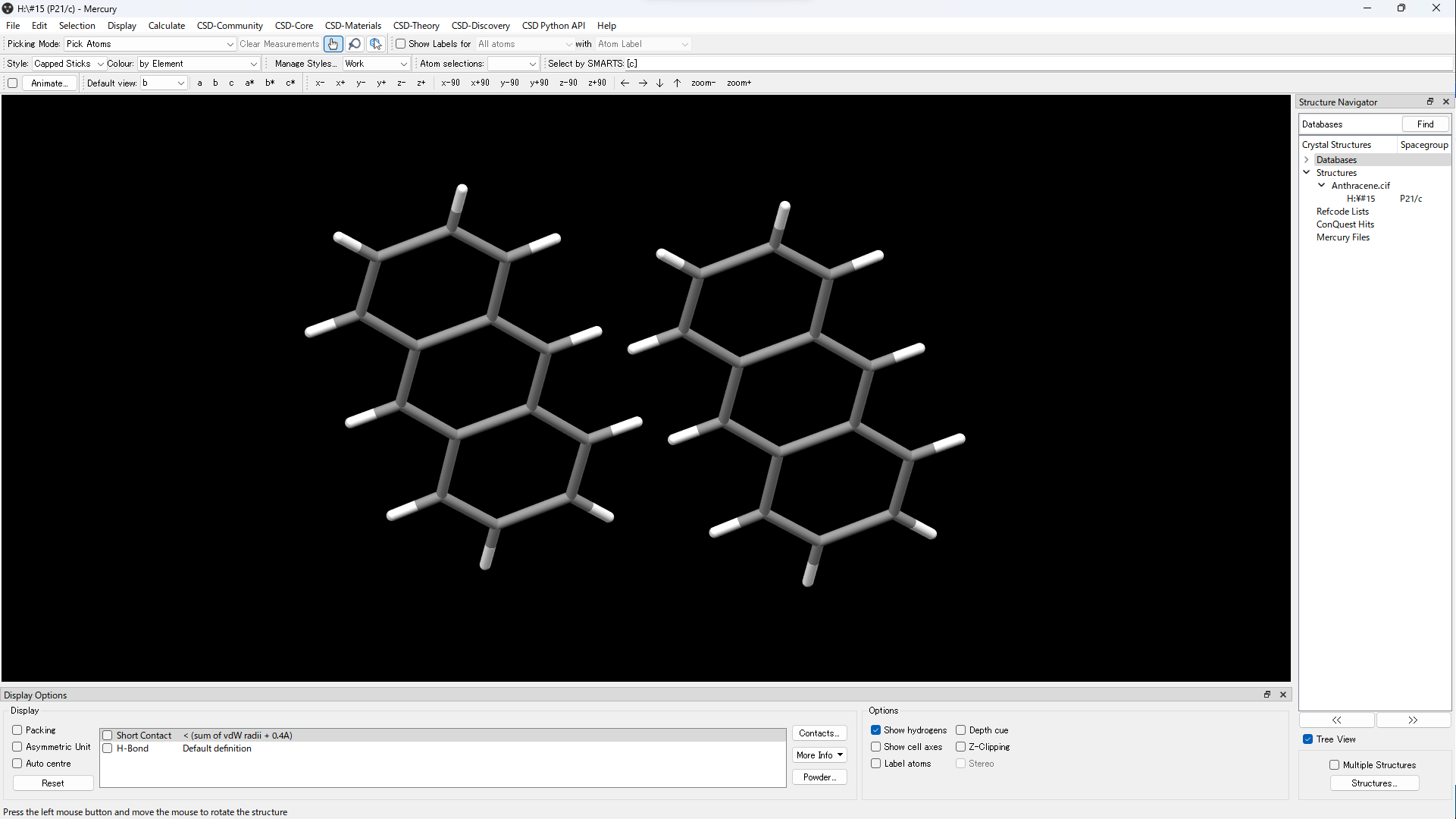
- Save in mol file or mol2 file.
- Open a mol file or mol2 file in GaussView and save it in gjf format.
Suppose the directory structure is as follows.
yyy
├── tcal.py
└── xxx.gjf
- Open a terminal.
- Go to the directory where the files is located.
cd yyy
- Execute the following command.
python tcal.py -a xxx.gjf- Execute the following command.
python tcal.py -cr xxx.gjf- Open xxx.fchk in GaussView.
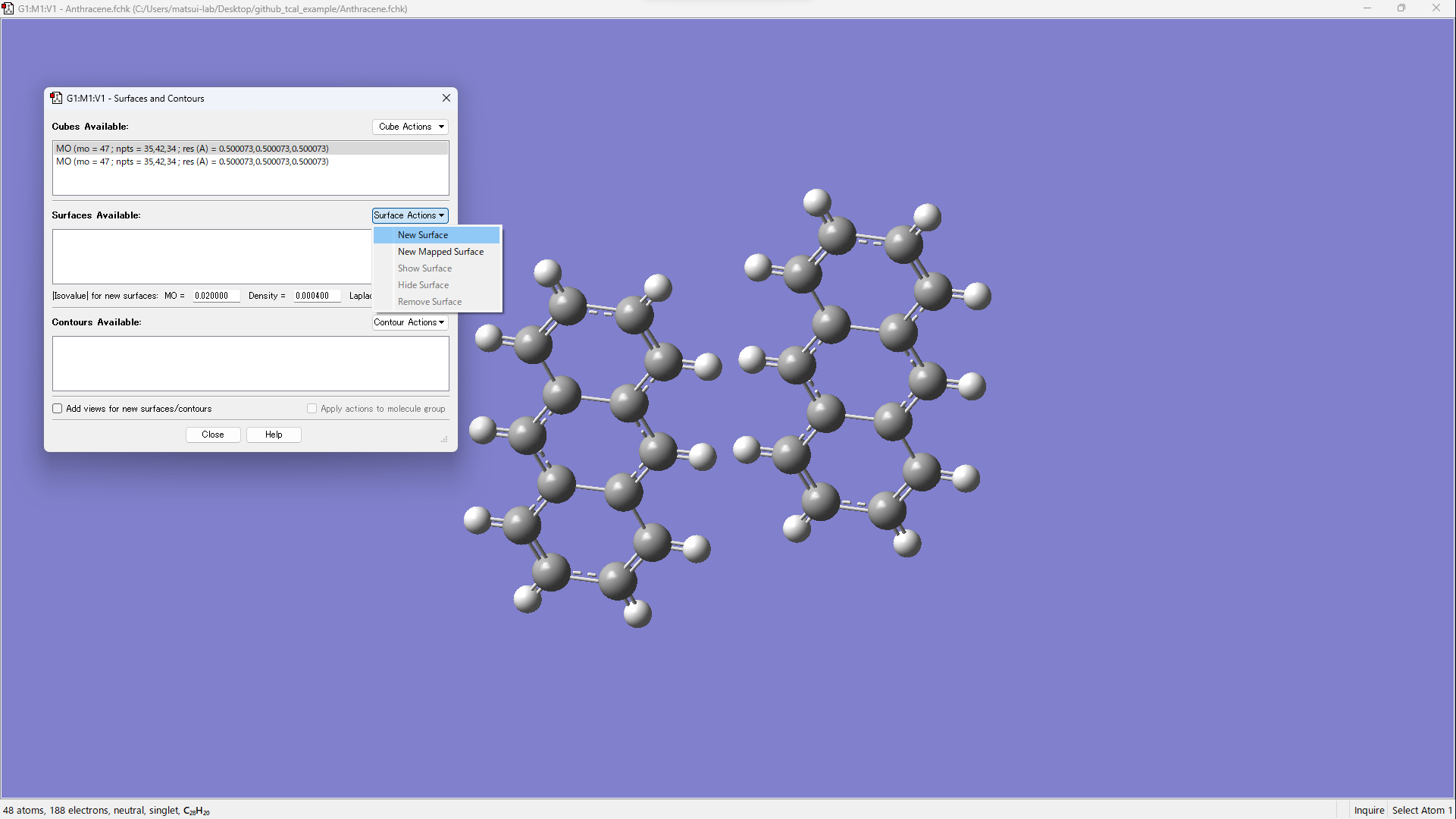
- [Results] → [Surfaces/Contours...]
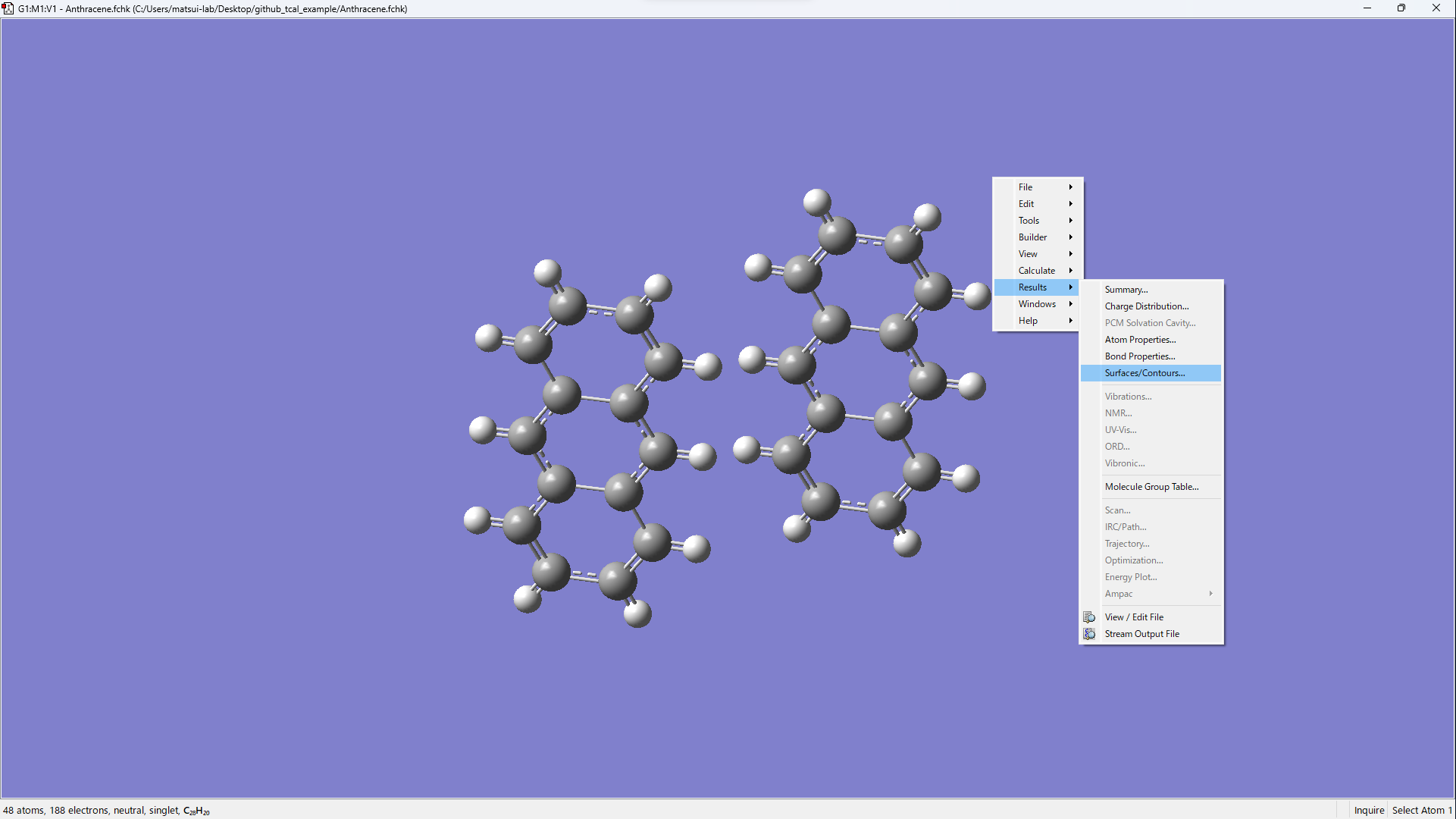
- [Cube Actions] → [Load Cube]
- Open xxx_m1_HOMO.cube and xxx_m2_HOMO.cube.
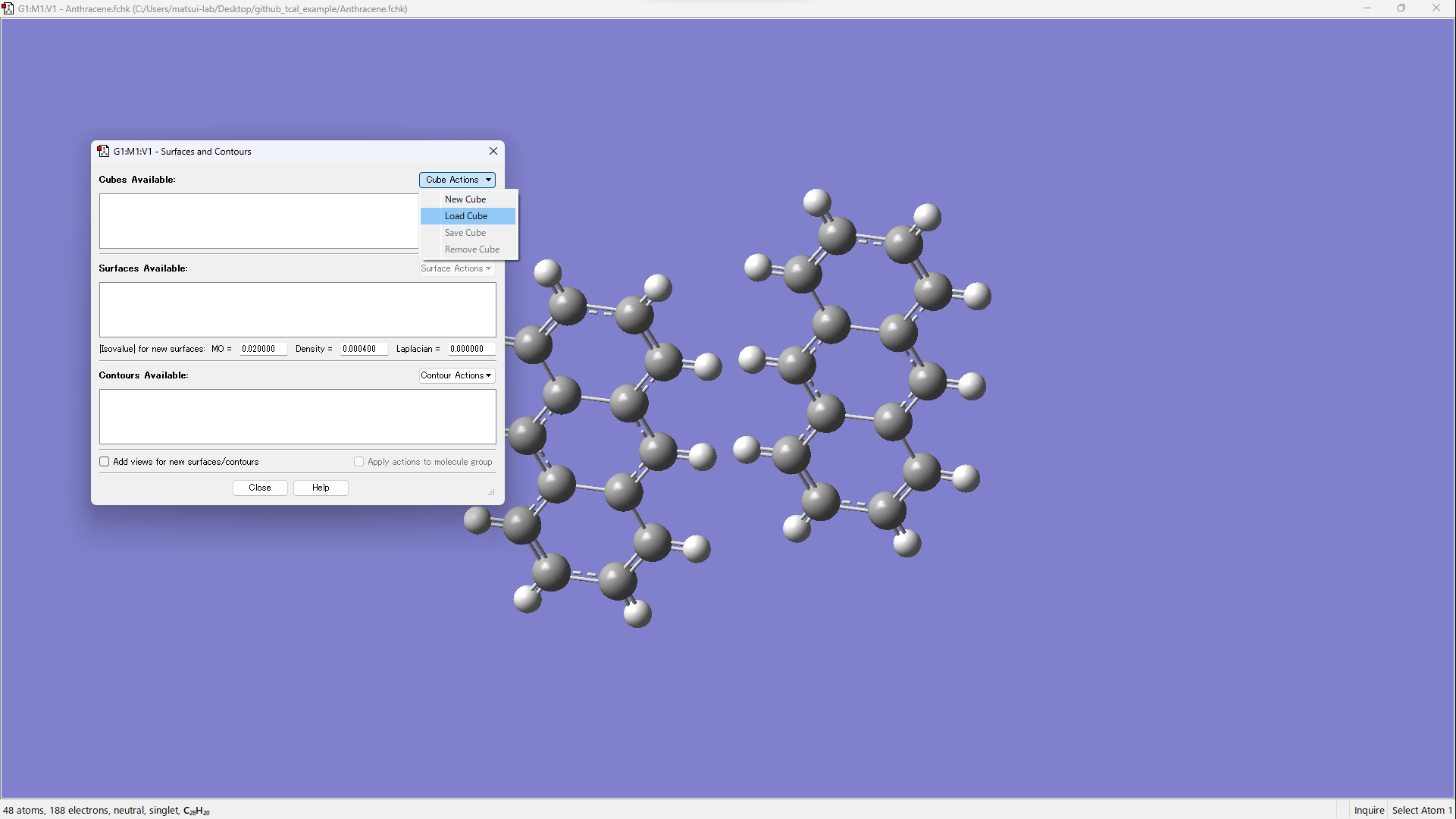
- Visualize by operating [Surface Actions] → [New Surface].
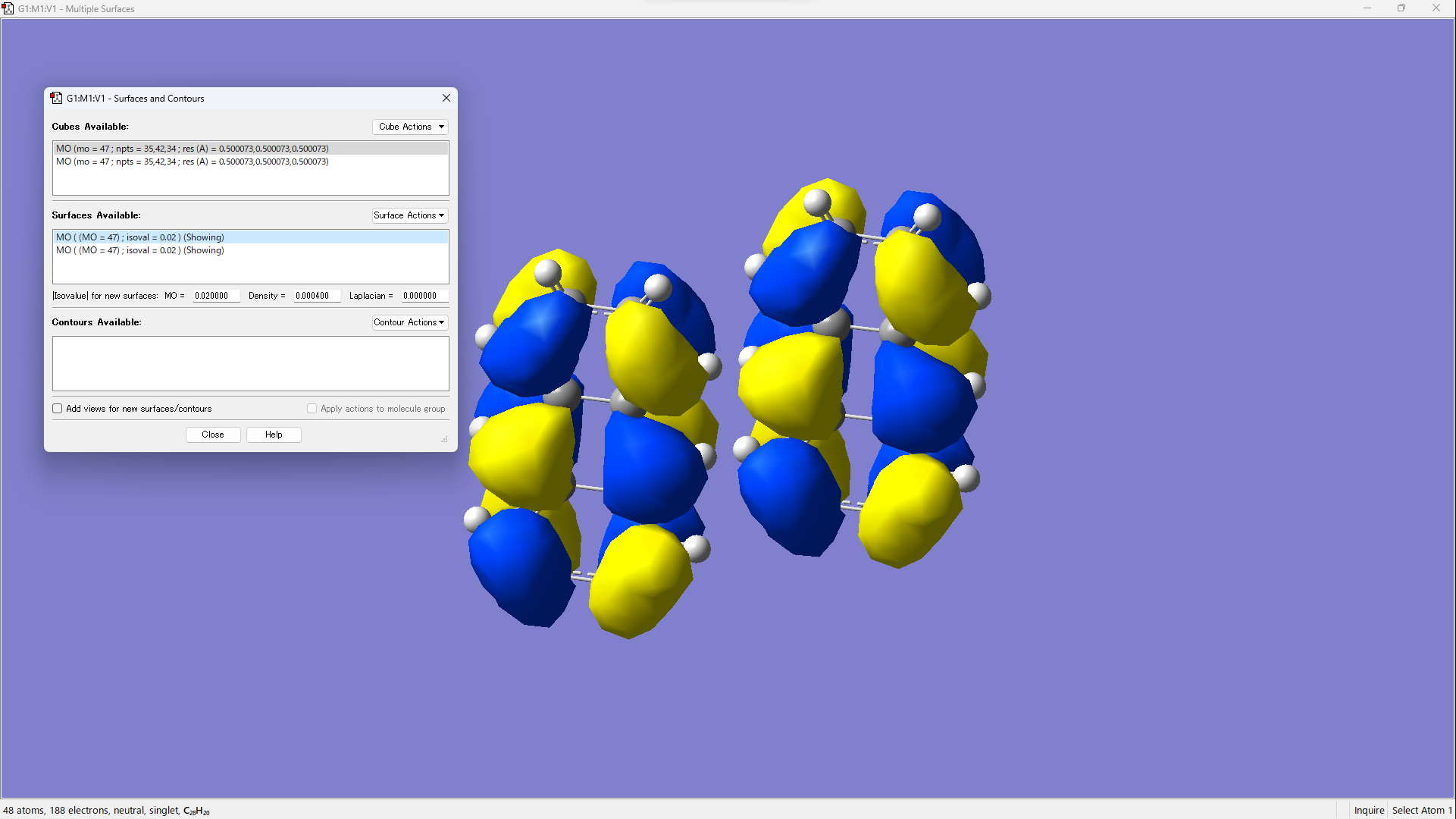
For calculating the transfer integral between molecule A and molecule B, DFT calculations were performed for monomer A, monomer B, and the dimer AB. The monomer molecular orbitals
where
In addition to the intermolecular transfer integral in general use, we developed an interatomic transfer integral for further analysis
where
Here we define the interatomic transfer integral
[1] Veaceslav Coropceanu et al., Charge Transport in Organic Semiconductors, Chem. Rev. 2007, 107, 926-952.
[2] Koki Ozawa et al., Statistical analysis of interatomic transfer integrals for exploring high-mobility organic semiconductors, Sci. Technol. Adv. Mater. 2024, 25, 2354652.
When publishing works that benefited from tcal, please cite the following article.
Koki Ozawa, Tomoharu Okada, Hiroyuki Matsui, Statistical analysis of interatomic transfer integrals for exploring high-mobility organic semiconductors, Sci. Technol. Adv. Mater., 2024, 25, 2354652.
DOI: 10.1080/14686996.2024.2354652
- Satoru Inoue et al., Regioisomeric control of layered crystallinity in solution-processable organic semiconductors, Chem. Sci. 2020, 11, 12493-12505.
- Toshiki Higashino et al., Architecting Layered Crystalline Organic Semiconductors Based on Unsymmetric π-Extended Thienoacenes, Chem. Mater. 2021, 33, 18, 7379–7385.
- Koki Ozawa et al., Statistical analysis of interatomic transfer integrals for exploring high-mobility organic semiconductors, Sci. Technol. Adv. Mater. 2024, 25, 2354652.
Matsui Laboratory, Research Center for Organic Electronics (ROEL), Yamagata University
Hiroyuki Matsui, Koki Ozawa
Email: h-matsui[at]yz.yamagata-u.ac.jp
Please replace [at] with @
This work was supported by JST, CREST, Grand Number JPMJCR18J2.


