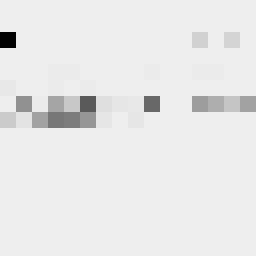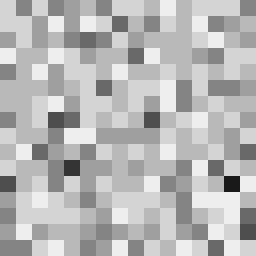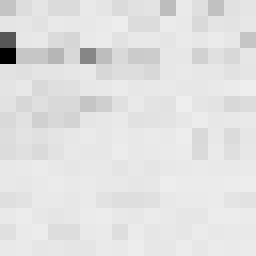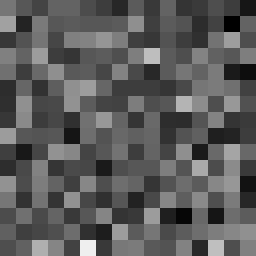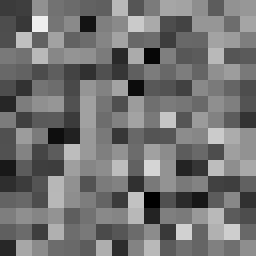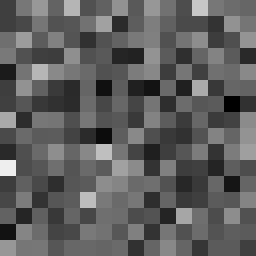Fast, secure, efficent stream cipher
Zci65 uses a 32-byte key and does not use an Initialization Vector (IV); the algorithm use a internal 256 length array s[] of 32 bit integer and other 2 internal 32 bit fields, k and c; in total the status size is 1088 bytes. The internal status is continuously changed by the source content to be encrypted. The code is very simple, the main functions are:
public byte encipher(byte b) {
int p = ((k >>> 24) ^ (k >>> 16) ^ (k >>> 8) ^ k) & 0xFF;
int r = s[p];
s[p] = k ^ (r << 2) ^ (r >>> 2);
k = s[(b + c++) & 0xFF] ^ (k << 2) ^ (k >>> 2);
return (byte)((r >>> 24) ^ (r >>> 16) ^ (r >>> 8) ^ r ^ b);
}
public byte decipher(byte b) {
int p = ((k >>> 24) ^ (k >>> 16) ^ (k >>> 8) ^ k) & 0xFF;
int t = s[p];
s[p] = k ^ (t << 2) ^ (t >>> 2);
int r = ((t >>> 24) ^ (t >>> 16) ^ (t >>> 8) ^ t ^ b) & 0xFF;
k = s[(r + c++) & 0xFF] ^ (k << 2) ^ (k >>> 2);
return (byte)r;
}The main properties of a good encryption algorithm are:
- Produce an output indistinguishable from a random sequence of bytes
- Do it in the shortest possible time (and this is especially true for a stream cipher)
- Make it impossible to predict the output sequence starting from the data already produced.
Point 1 can be verified with statistical analysis; point 2 by measuring the times and comparing them with benchmark values, while point 3 can only be verified by an independent cryptographic analysis and therefore I invite the researchers to consider zci65 and confirm or deny this feature!
This tool shows the byte distribution of a file on a square window displaying a 16x16 matrix (one element for each byte). The least frequent byte is displayed in white, the most frequent byte in black, the others are proportionally distributed in shades of gray (total 256 shades). The result is that a tendentially dark image corresponds to a higher chaotic level of the analyzed data. A good indicator of the degree of chaos of a sequence of bytes (cryptographic output) is the estimate of pi: each successive sequence of six bytes is used as 24 bit X and Y co-ordinates within a square. If the distance of the randomly-generated point is less than the radius of a circle inscribed within the square, the six-byte sequence is considered a “hit”. The percentage of hits is used to calculate the value of Pi.
In this case the file was zipped with the maximum compression level and also encrypted with a password (AES-256 algorithm). The statistical indicators and the degree of darkness of the images are very close.
The following tables show the values of byte frequency tests (Standard Deviation, Chi Squared, Coefficient of Variation and Mean Bytes Value) and distribution-dependent test (Monte Carlo Pi 2D, Monte Carlo PI 3D, Mean of All Adjacent Byte Pairs and Number of Collisions 4 bytes, calculated by analyzing 1,000 output arrays produced from 1 input array with 1,000,000 random keys by the zci65 and salsa20 algorithms. As a benchmark, the same indices were calculated on a sample of 1,000,000 random arrays. For more information about test see: https://github.com/matteo65/VisualRT
| Index | zci65 | salsa20 | benchmark |
|---|---|---|---|
| Min Standard Dev. min(σ) | 50.664 | 49.544 | 49.406 |
| Max Standard Dev. max(σ) | 74.976 | 75.912 | 78.532 |
| Average Standard Dev. avg(σ) | 62.315 | 62.318 | 62.320 |
| Min Chi Squared min(𝛘2) | 168.223 | 160.862 | 159.968 |
| Max Chi Squared max(𝛘2) | 368.408 | 377.662 | 404.176 |
| Average Chi squared avg(𝛘2) | 254.987 | 255.013 | 255.030 |
| Min Coef.of Variation min(σ/μ) | 1.297% | 1.268% | 1.265% |
| Max Coef.of Variation max(σ/μ) | 1.919% | 1.943% | 2.010% |
| Average Coef. of Variation avg(σ/μ) | 1.595% | 1.595% | 1.595% |
| Index | zci65 | salsa20 | benchmark |
|---|---|---|---|
| Min Standard Dev. min(σ) | 48.189 | 49.544 | 49.406 |
| Max Standard Dev. max(σ) | 77.811 | 75.912 | 78.532 |
| Average Standard Dev. avg(σ) | 62.311 | 62.318 | 62.320 |
| Min Chi Squared min(𝛘2) | 152.186 | 160.862 | 159.968 |
| Max Chi Squared max(𝛘2) | 396.791 | 377.662 | 404.176 |
| Average Chi squared avg(𝛘2) | 254.95 | 255.013 | 255.030 |
| Min Coef.of Variation min(σ/μ) | 1.234% | 1.268% | 1.265% |
| Max Coef.of Variation max(σ/μ) | 1.992% | 1.943% | 2.010% |
| Average Coef. of Variation avg(σ/μ) | 1.595% | 1.595% | 1.595% |
| Index | zci65 | salsa20 | benchmark |
|---|---|---|---|
| Min Standard Dev. min(σ) | 49.570 | 50.401 | 49.406 |
| Max Standard Dev. max(σ) | 77.763 | 75.819 | 78.532 |
| Average Standard Dev. avg(σ) | 62.310 | 62.316 | 62.320 |
| Min Chi Squared min(𝛘2) | 161.035 | 166.481 | 159.968 |
| Max Chi Squared max(𝛘2) | 396.303 | 376.735 | 404.176 |
| Average Chi squared avg(𝛘2) | 254.944 | 254.991 | 255.030 |
| Min Coef.of Variation min(σ/μ) | 1.269% | 1.290% | 1.265% |
| Max Coef.of Variation max(σ/μ) | 1.991% | 1.941% | 2.010% |
| Average Coef. of Variation avg(σ/μ) | 1.595% | 1.595% | 1.595% |
zci65 can be considered a valid alternative in implementations that require a fast and secure streaming encryption algorithm.