A python library to compute power indices
Installation:
pip install powerindexYoutube: Short overview
Google colab: colab
Calculation of power indices. Example of CLI ("px" alias) run (EEC in 1957 ):
# EEC (1958-1982): Germany, France, Italy, Netherlands, Belgium, Luxemburg
px -i b -q 12 -w 4 4 4 2 2 1
# expected result:
# 0.23809523809523808,0.23809523809523808,0.23809523809523808,0.14285714285714285,0.14285714285714285,0.0The aim of the package is to compute different power indices of the so-called weighted voting systems (games).
Players have weights and can form coalitions. A coalition that achieves the required threshold wins.
To start with a simple example, consider a system with two parties A and B having 51 and 49 seats respectively with a simple majority rule (i.e. the threshold is 51 seats). How much power do they have? It may appear that according to the number of the seats they have 51% and 49% respectively.
However, party A can impose any decision without cooperating with party B.
It leads to a conclusion that any reasonable rule would assign to party A 100% of the power (since it wins without cooperation) and to the party B 0% of the power and not 51% to 49%.
The most popular approaches to measure power are Banzhaf and Shapley-Shubik power indices.
This package also implements the Contested Garment Rule (strictly speaking it's not a power index, but similar to some extent).
It can be run either as a command line (px) or in python interpreter. CLI run:
px -i b -q 4 -w 3 2 1 Flags: -i (index) is either 'b' for Banzhaf, or 'ss' for Shapley-Shubik. -q (quota) number of votes for a coalition to win. -w (weights) weights of players.
There's a jupyter notebook /powerindex/README.ipynb that shows some python examples.
A trivial example from the introduction:
#bash
px -i b -q 51 -w 51 49
px -i ss -q 51 -w 51 49 #python
#%matplotlib inline
import powerindex as px
game=px.Game(quota=51,weights=[51,49])Calculation of Banzhaf and Shapley-Shubik power indices:
#python
game.calc_banzhaf()
print(game.banzhaf)[1.0, 0.0]
#python
game.calc_shapley_shubik()
print(game.shapley_shubik)[1.0, 0.0]
Function calc() computes all available indices.
Thus, in this simple example both indices give 100% to 0% distribution.
Now let's changes the seats distribution to the parity and see what happens:
#bash
px -i b -q 51 -w 50 50
px -i ss -q 51 -w 50 50 #python
game=px.Game(51,weights=[50,50])
game.calc()
print(game.banzhaf)
print(game.shapley_shubik)[0.5, 0.5]
[0.5, 0.5]
As the result, the distribution of power is also at parity.
Now, consider a non-trivial, but still a simple examples from Wikipedia:
#bash
px -i b -q 6 -w 4 3 2 1 #python
game=px.Game(6,[4, 3, 2, 1])
game.calc_banzhaf()
print(game.banzhaf)[0.4166666666666667, 0.25, 0.25, 0.08333333333333333]
Interpretation is simple. A committee where 4 parties hold 40%, 30%, 20% and 10% of seats with required qualified majority of 60%, have 41.7%, 25%, 25%, 8.3% of power respectively.
In this example, having 2 or 3 seats leads to the same level of power.
Another example:
#bash
px -i b -q 6 -w 3 2 1 1 #python
game=px.Game(6,[3, 2, 1, 1])
game.calc_banzhaf()
print(game.banzhaf)[0.375, 0.375, 0.125, 0.125]
Notice that in the previous two examples Banzhaf and Shapley-Shubik indices coincides. It doesn't hold in general even in the games of 3 voters:
#bash
px -i ss -q 6 -w 3 2 1 1 #python
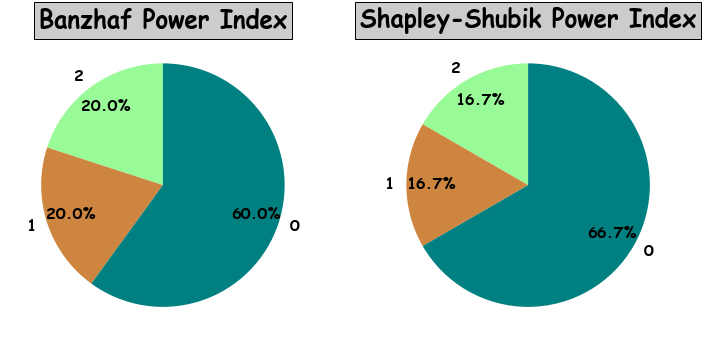
game=px.Game(4,[3, 2, 1])
game.calc() # again it calculates all available indices
print("Banzhaf index:")
print(game.banzhaf)
print("Shapley-Shubik index:")
print(game.shapley_shubik)Banzhaf index:
[0.6, 0.2, 0.2]
Shapley-Shubik index:
[0.6666666666666667, 0.16666666666666669, 0.16666666666666669]
Not exactly a power index, but similar to some extent. Contested Garment Rule offers a way to split the value of the contested asset when its value is smaller than the some of claims. It's different from the proportional rule.
e.g. if the claims are 100, 200 and 300 (i.e. 600 in sum) among three participants, and there's only 210 to split, the rule suggests the split 50, 80, 80 (and not 35, 70, 105).
Note the flag -a (absolute) to generate the split in the absolute numbers.
!px -i cg -q 210 -a -w 100 200 300game=px.Game(210,[100, 200, 300], absolute=True)
game.calc_contested_garment()
print(game.contested_garment)[50.0, 80.0, 80.0]
There's a possibility to plot the power distribution as a pie chart:
#python
game=px.Game(4,[3, 2, 1])
game.calc()
game.pie_chart()As you can see on the plot, the parties have numbers. In order, to put their names on the chart you need to work with Party class.
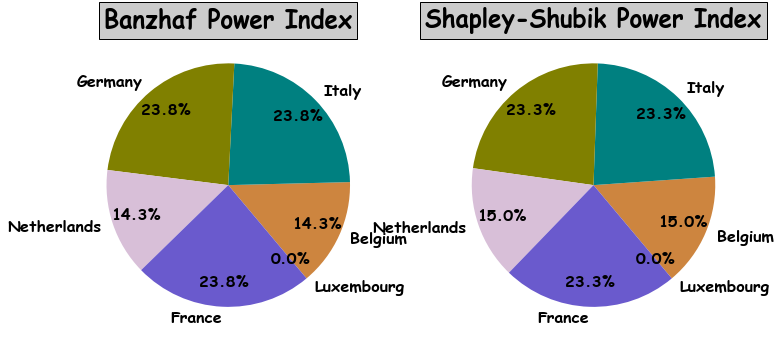
Let's take Europen Economic Community (EEC) in the years 1958-1972, its members were Germany (4 votes), France (4 votes), Italy (4 votes), Belgium (2 votes), Netherlands (2 votes) and Luxembourg (1 vote) with qualified majority of 12 votes:
#python
countries={"Germany":4,"France":4,"Italy":4,"Belgium":2,"Netherlands":2,"Luxembourg":1}
parties=[px.Party(countries[country],country) for country in countries]
game=px.Game(12,parties=parties)
game.calc()
game.pie_chart()Usually the exact and fast computation of indices is based on enumeration methods implemented by dynamic programming given that the weights and thresholds are integers.
For instance, the computation of Banzhaf is O(qn) hard and computation of Shapley-Shubik is O(qn^2) hard. If the input has non-integers, then an approximation scheme is usually involved. Consult the list of literature if you want to start exploring the topic by yourself.
B.Keijzer - A Survey on the Computation of Power Indices (2008)
T.Uno - Efficient Computation of Power Indices for Weighted Majority Games (2003)
Matsui, Y. Matsui - A Survey of Algorithms for Calculating Power Indices of Weighted Majority Games (2000)
B.Meglicki - Generating functions partitioning algorithm for computing power indices in weighted voting games (2010)
Zyczkowski, W. Slomczynski - Voting in the European Union: the square root system of Penrose and a critical point (2004)
@misc{powerindex2024,
author = {Maxim Litvak},
title = {powerindex: A Python Library for Calculation of Some Common Power Indices},
year = {2024}, % Year of the version or first release, as appropriate
version = {0.2.4},
howpublished = {\url{https://github.com/maxlit/powerindex}},
}