This is an advanced tutorial on Image Colorization using deep learning and PyTorch.
This is the related article on TowardsDataScince by myself which you can check out. I've put the explanations here as well but one could prefer to read it from the article.
I highly recommend that you go through this tutorial in colab by simply clicking the Open in Colab badge below. You can train the models from scratch or downlaod the pretrained weights and use it to colorize your black & white images. All the tutorial explanations are included there as well.
Left: Input black & white images from test set | Right: the colorized outputs by the final model of this tutorialLeft: Input black & white images from test set | Right: the colorized outputs by the final model of this tutorial
Left: Input black & white images from test set | Right: the colorized outputs by the final model of this tutorial
One of the most exciting applications of deep learning is colorizing black and white images. This task needed a lot of human input and hardcoding several years ago but now the whole process can be done end-to-end with the power of AI and deep learning. You might think that you need huge amount of data or long training times to train your model from scratch for this task but in the last few weeks I worked on this and tried many different model architectures, loss functions, training strategies, etc. and finally developed an efficient strategy to train such a model, using the latest advances in deep learning, on a rather small dataset and with really short training times. In this article, I'm going to explain what I did to make this happen, including the code!, and the strategies that helped and also those that were not useful. Before that, I will explain the colorization problem and a give you a short review of what has been done in recent years. I'll assume you have basic knowledge about deep learning, GANs, and PyTorch library for the rest of the article. Let's begin!
Here I'm going to give you some basic knowledge that you may need to understand what the models do in the following codes.
As you might know, when we load an image, we get a rank-3 (height, width, color) array with the last axis containing the color data for our image. These data represent color in RGB color space and there are 3 numbers for each pixel indicating how much Red, Green, and Blue the pixel is. In the following image you can see that in the left part of the "main image" (the leftmost image) we have blue color so in the blue channel of the image, that part has higher values and has turned dark.
In L*a*b color space, we have again three numbers for each pixel but these numbers have different meanings. The first number (channel), L, encodes the Lightness of each pixel and when we visualize this channel (the second image in the row below) it appears as a black and white image. The *a and *b channels encode how much green-red and yellow-blue each pixel is, respectively. In the following image you can see each channel of L*a*b color space separately.
In all papers I studied and all codes I checked out on colorization on GitHub, people use L*a*b color space instead of RGB to train the models. There are a couple of reasons for this choice but I'll give you an intuition of why we make this choice. To train a model for colorization, we should give it a grayscale image and hope that it will make it colorful. When using L*a*b, we can give the L channel to the model (which is the grayscale image) and want it to predict the other two channels (*a, *b) and after its prediction, we concatenate all the channels and we get our colorful image. But if you use RGB, you have to first convert your image to grayscale, feed the grayscale image to the model and hope it will predict 3 numbers for you which is a way more difficult and unstable task due to the many more possible combinations of 3 numbers compared to two numbers. If we assume we have 256 choices (in a 8-bit unsigned integer image this is the real number of choices) for each number, predicting the three numbers for each of the pixels is choosing between 256³ combinations which is more than 16 million choices, but when predicting two numbers we have about 65000 choices (actually, we are not going to wildly choose these numbers like a classification task and I just wrote these numbers to give you an intuition).
During the last few years, many different solutions have been proposed to colorize images by using deep learning. Colorful Image Colorization paper approached the problem as a classification task and they also considered the uncertainty of this problem (e.x. a car in the image can take on many different and valid colors and we cannot be sure about any color for it); however, another paper approached the problem as a regression task (with some more tweaks!). There are pros and cons to each approach but in this article, we are going to use a different strategy.
Image-to-Image Translation with Conditional Adversarial Networks paper, which you may know by the name pix2pix, proposed a general solution to many image-to-image tasks in deep learning which one of those was colorization. In this approach two losses are used: L1 loss, which makes it a regression task, and an adversarial (GAN) loss, which helps to solve the problem in an unsupervised manner (by assigning the outputs a number indicating how "real" they look!).
In this tutorial, I will first implement what the authors did in the paper and then I will introduce a whole new generator model and some tweaks in the strategy of training which significantly helps reduce the size of needed dataset while getting amazing results. So stay tuned :)
As mentioned earlier, we are going to build a GAN (a conditional GAN to be specific) and use an extra loss function, L1 loss. Let's start with the GAN.
As you might know, in a GAN we have a generator and a discriminator model which learn to solve a problem together. In our setting, the generator model takes a grayscale image (1-channel image) and produces a 2-channel image, a channel for *a and another for *b. The discriminator, takes these two produced channels and concatenates them with the input grayscale image and decides whether this new 3-channel image is fake or real. Of course the discriminator also needs to see some real images (3-channel images again in Lab color space) that are not produced by the generator and should learn that they are real.
So what about the "condition" we mentioned? Well, that grayscale image which both the generator and discriminator see is the condition that we provide to both models in our GAN and expect that the they take this condition into consideration.
Let's take a look at the math. Consider x as the grayscale image, z as the input noise for the generator, and y as the 2-channel output we want from the generator (it can also represent the 2 color channels of a real image). Also, G is the generator model and D is the discriminator. Then the loss for our conditional GAN will be:
Notice that x is given to both models which is the condition we introduce two both players of this game. Actually, we are not going to feed a "n" dimensional vector of random noise to the generator as you might expect but the noise is introduced in the form of dropout layers (there is something cool about it which you will read in the last section of the article) in the generator architecture.
The earlier loss function helps to produce good-looking colorful images that seem real, but to further help the models and introduce some supervision in our task, we combine this loss function with L1 Loss (you might know L1 loss as mean absolute error) of the predicted colors compared with the actual colors:
If we use L1 loss alone, the model still learns to colorize the images but it will be conservative and most of the time uses colors like "gray" or "brown" because when it doubts which color is the best, it takes the average and uses these colors to reduce the L1 loss as much as possible (it is similar to the blurring effect of L1 or L2 loss in super resolution task). Also, the L1 Loss is preferred over L2 loss (or mean squared error) because it reduces that effect of producing gray-ish images. So, our combined loss function will be:
where λ is a coefficient to balance the contribution of the two losses to the final loss (of course the discriminator loss does not involve the L1 loss).
Okay. I think it's enough for theory! Let's get our hands dirty with the code! In the following section, I first introduce the code to implement the paper and in the section after that, I will introduce a better strategy to get really amazing results in one or two hours of training and without needing huge amount of data!
The paper uses the whole ImageNet dataset (with 1.3 million images!) but here I'm using only 8,000 images from COCO dataset for training which I had available on my device. So our training set size is 0.6% of what was used in the paper! You can use almost any dataset for this task as far as it contains many different scenes and locations which you hope it will learn to colorize. You can use ImageNet for example but you will only need 8000 of its images for this project.
import os
import glob
import time
import numpy as np
from PIL import Image
from pathlib import Path
from tqdm.notebook import tqdm
import matplotlib.pyplot as plt
from skimage.color import rgb2lab, lab2rgb
Path.ls = lambda x: list(x.iterdir())
import torch
from torch import nn, optim
from torchvision import transforms
from torchvision.utils import make_grid
from torch.utils.data import Dataset, DataLoader
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")paths = glob.glob("/datasets/coco/*.jpg") # Your path for your dataset
np.random.seed(123)
paths_subset = np.random.choice(paths, 10_000, replace=False) # choosing 1000 images randomly
rand_idxs = np.random.permutation(10_000)
train_idxs = rand_idxs[:8000] # choosing the first 8000 as training set
val_idxs = rand_idxs[8000:] # choosing last 2000 as validation set
train_paths = paths_subset[train_idxs]
val_paths = paths_subset[val_idxs]
print(len(train_paths), len(val_paths))_, axes = plt.subplots(4, 4, figsize=(10, 10))
for ax, img_path in zip(axes.flatten(), train_paths):
ax.imshow(Image.open(img_path))
ax.axis("off")I hope the code is self-explanatory. I'm resizing the images and flipping horizontally (flipping only if it is training set) and then I read an RGB image, convert it to Lab color space and separate the first (grayscale) channel and the color channels as my inputs and targets for the models respectively. Then I'm making the data loaders.
SIZE = 256
class ColorizationDataset(Dataset):
def __init__(self, paths, split='train'):
if split == 'train':
self.transforms = transforms.Compose([
transforms.Resize((SIZE, SIZE), Image.BICUBIC),
transforms.RandomHorizontalFlip(), # A little data augmentation!
])
elif split == 'val':
self.transforms = transforms.Resize((SIZE, SIZE), Image.BICUBIC)
self.split = split
self.size = SIZE
self.paths = paths
def __getitem__(self, idx):
img = Image.open(self.paths[idx]).convert("RGB")
img = self.transforms(img)
img = np.array(img)
img_lab = rgb2lab(img).astype("float32") # Converting RGB to L*a*b
img_lab = transforms.ToTensor()(img_lab)
L = img_lab[[0], ...] / 50. - 1. # Between -1 and 1
ab = img_lab[[1, 2], ...] / 110. # Between -1 and 1
return {'L': L, 'ab': ab}
def __len__(self):
return len(self.paths)
def make_dataloaders(batch_size=16, n_workers=4, pin_memory=True, **kwargs): # A handy function to make our dataloaders
dataset = ColorizationDataset(**kwargs)
dataloader = DataLoader(dataset, batch_size=batch_size, num_workers=n_workers,
pin_memory=pin_memory)
return dataloadertrain_dl = make_dataloaders(paths=train_paths, split='train')
val_dl = make_dataloaders(paths=val_paths, split='val')
data = next(iter(train_dl))
Ls, abs_ = data['L'], data['ab']
print(Ls.shape, abs_.shape)
print(len(train_dl), len(val_dl))This one is a little complicated and needs explanation. This code implements a U-Net to be used as the generator of our GAN. The details of the code are out of the scope of this article but the important thing to understand is that it makes the U-Net from the middle part of it (down in the U shape) and adds down-sampling and up-sampling modules to the left and right of that middle module (respectively) at every iteration until it reaches the input module and output module. Look at the following image that I made from one of the images in the article to give you a better sense of what is happening in the code:
The blue rectangles show the order in which the related modules are built with the code. The U-Net we will build has more layers than what is depicted in this image but it suffices to give you the idea. Also notice in the code that we are going 8 layers down, so if we start with a 256 by 256 image, in the middle of the U-Net we will get a 1 by 1 (256 / 2⁸) image and then it gets up-sampled to produce a 256 by 256 image (with two channels). This code snippet is really exciting and I highly recommend to play with it to fully grasp what every line of it is doing.
class UnetBlock(nn.Module):
def __init__(self, nf, ni, submodule=None, input_c=None, dropout=False,
innermost=False, outermost=False):
super().__init__()
self.outermost = outermost
if input_c is None: input_c = nf
downconv = nn.Conv2d(input_c, ni, kernel_size=4,
stride=2, padding=1, bias=False)
downrelu = nn.LeakyReLU(0.2, True)
downnorm = nn.BatchNorm2d(ni)
uprelu = nn.ReLU(True)
upnorm = nn.BatchNorm2d(nf)
if outermost:
upconv = nn.ConvTranspose2d(ni * 2, nf, kernel_size=4,
stride=2, padding=1)
down = [downconv]
up = [uprelu, upconv, nn.Tanh()]
model = down + [submodule] + up
elif innermost:
upconv = nn.ConvTranspose2d(ni, nf, kernel_size=4,
stride=2, padding=1, bias=False)
down = [downrelu, downconv]
up = [uprelu, upconv, upnorm]
model = down + up
else:
upconv = nn.ConvTranspose2d(ni * 2, nf, kernel_size=4,
stride=2, padding=1, bias=False)
down = [downrelu, downconv, downnorm]
up = [uprelu, upconv, upnorm]
if dropout: up += [nn.Dropout(0.5)]
model = down + [submodule] + up
self.model = nn.Sequential(*model)
def forward(self, x):
if self.outermost:
return self.model(x)
else:
return torch.cat([x, self.model(x)], 1)
class Unet(nn.Module):
def __init__(self, input_c=1, output_c=2, n_down=8, num_filters=64):
super().__init__()
unet_block = UnetBlock(num_filters * 8, num_filters * 8, innermost=True)
for _ in range(n_down - 5):
unet_block = UnetBlock(num_filters * 8, num_filters * 8, submodule=unet_block, dropout=True)
out_filters = num_filters * 8
for _ in range(3):
unet_block = UnetBlock(out_filters // 2, out_filters, submodule=unet_block)
out_filters //= 2
self.model = UnetBlock(output_c, out_filters, input_c=input_c, submodule=unet_block, outermost=True)
def forward(self, x):
return self.model(x)The architecture of our discriminator is rather straight forward. This code implements a model by stacking blocks of Conv-BatchNorm-LeackyReLU to decide whether the input image is fake or real. Notice that the first and last blocks do not use normalization and the last block has no activation function (it is embedded in the loss function we will use).
class PatchDiscriminator(nn.Module):
def __init__(self, input_c, num_filters=64, n_down=3):
super().__init__()
model = [self.get_layers(input_c, num_filters, norm=False)]
model += [self.get_layers(num_filters * 2 ** i, num_filters * 2 ** (i + 1), s=1 if i == (n_down-1) else 2)
for i in range(n_down)] # the 'if' statement is taking care of not using
# stride of 2 for the last block in this loop
model += [self.get_layers(num_filters * 2 ** n_down, 1, s=1, norm=False, act=False)] # Make sure to not use normalization or
# activation for the last layer of the model
self.model = nn.Sequential(*model)
def get_layers(self, ni, nf, k=4, s=2, p=1, norm=True, act=True): # when needing to make some repeatitive blocks of layers,
layers = [nn.Conv2d(ni, nf, k, s, p, bias=not norm)] # it's always helpful to make a separate method for that purpose
if norm: layers += [nn.BatchNorm2d(nf)]
if act: layers += [nn.LeakyReLU(0.2, True)]
return nn.Sequential(*layers)
def forward(self, x):
return self.model(x)Let's take a look at its blocks:
PatchDiscriminator(3)And its output shape:
discriminator = PatchDiscriminator(3)
dummy_input = torch.randn(16, 3, 256, 256) # batch_size, channels, size, size
out = discriminator(dummy_input)
out.shapeWe are using a "Patch" Discriminator here. Okay, what is it?! In a vanilla discriminator, the model outputs one number (a scaler) which represents how much the model thinks the input (which is the whole image) is real (or fake). In a patch discriminator, the model outputs one number for every patch of say 70 by 70 pixels of the input image and for each of them decides whether it is fake or not separately. Using such a model for the task of colorization seems reasonable to me because the local changes that the model needs to make are really important and maybe deciding on the whole image as in vanilla discriminator cannot take care of the subtleties of this task. Here, the model's output shape is 30 by 30 but it does not mean that our patches are 30 by 30. The actual patch size is obtained when you compute the receptive field of each of these 900 (30 multiplied by 30) output numbers which in our case will be 70 by 70.
This is a handy class we can use to calculate the GAN loss of our final model. In the init we decide which kind of loss we're going to use (which will be "vanilla" in our project) and register some constant tensors as the "real" and "fake" labels. Then when we call this module, it makes an appropriate tensor full of zeros or ones (according to what we need at the stage) and computes the loss.
class GANLoss(nn.Module):
def __init__(self, gan_mode='vanilla', real_label=1.0, fake_label=0.0):
super().__init__()
self.register_buffer('real_label', torch.tensor(real_label))
self.register_buffer('fake_label', torch.tensor(fake_label))
if gan_mode == 'vanilla':
self.loss = nn.BCEWithLogitsLoss()
elif gan_mode == 'lsgan':
self.loss = nn.MSELoss()
def get_labels(self, preds, target_is_real):
if target_is_real:
labels = self.real_label
else:
labels = self.fake_label
return labels.expand_as(preds)
def __call__(self, preds, target_is_real):
labels = self.get_labels(preds, target_is_real)
loss = self.loss(preds, labels)
return lossIn the TowardsDataScince article, I didn't explain this function. Here is our logic to initialize our models. We are going to initialize the weights of our model with a mean of 0.0 and standard deviation of 0.02 which are the proposed hyperparameters in the article:
def init_weights(net, init='norm', gain=0.02):
def init_func(m):
classname = m.__class__.__name__
if hasattr(m, 'weight') and 'Conv' in classname:
if init == 'norm':
nn.init.normal_(m.weight.data, mean=0.0, std=gain)
elif init == 'xavier':
nn.init.xavier_normal_(m.weight.data, gain=gain)
elif init == 'kaiming':
nn.init.kaiming_normal_(m.weight.data, a=0, mode='fan_in')
if hasattr(m, 'bias') and m.bias is not None:
nn.init.constant_(m.bias.data, 0.0)
elif 'BatchNorm2d' in classname:
nn.init.normal_(m.weight.data, 1., gain)
nn.init.constant_(m.bias.data, 0.)
net.apply(init_func)
print(f"model initialized with {init} initialization")
return net
def init_model(model, device):
model = model.to(device)
model = init_weights(model)
return modelThis class brings together all the previous parts and implements a few methods to take care of training our complete model. Let's investigate it.
In the init we define our generator and discriminator using the previous functions and classes we defined and we also initialize them with init_model function which I didn't explain here but you can refer to my GitHub repository to see how it works. Then we define our two loss functions and the optimizers of the generator and discriminator.
The whole work is being done in optimize method of this class. First and only once per iteration (batch of training set) we call the module's forward method and store the outputs in fake_color variable of the class.
Then, we first train the discriminator by using backward_D method in which we feed the fake images produced by generator to the discriminator (make sure to detach them from the generator's graph so that they act as a constant to the discriminator, like normal images) and label them as fake. Then we feed a batch of real images from training set to the discriminator and label them as real. We add up the two losses for fake and real and take the average and then call the backward on the final loss. Now, we can train the generator. In backward_G method we feed the discriminator the fake image and try to fool it by assigning real labels to them and calculating the adversarial loss. As I mentioned earlier, we use L1 loss as well and compute the distance between the predicted two channels and the target two channels and multiply this loss by a coefficient (which is 100 in our case) to balance the two losses and then add this loss to the adversarial loss. Then we call the backward method of the loss.
class MainModel(nn.Module):
def __init__(self, net_G=None, lr_G=2e-4, lr_D=2e-4,
beta1=0.5, beta2=0.999, lambda_L1=100.):
super().__init__()
self.device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
self.lambda_L1 = lambda_L1
if net_G is None:
self.net_G = init_model(Unet(input_c=1, output_c=2, n_down=8, num_filters=64), self.device)
else:
self.net_G = net_G.to(self.device)
self.net_D = init_model(PatchDiscriminator(input_c=3, n_down=3, num_filters=64), self.device)
self.GANcriterion = GANLoss(gan_mode='vanilla').to(self.device)
self.L1criterion = nn.L1Loss()
self.opt_G = optim.Adam(self.net_G.parameters(), lr=lr_G, betas=(beta1, beta2))
self.opt_D = optim.Adam(self.net_D.parameters(), lr=lr_D, betas=(beta1, beta2))
def set_requires_grad(self, model, requires_grad=True):
for p in model.parameters():
p.requires_grad = requires_grad
def setup_input(self, data):
self.L = data['L'].to(self.device)
self.ab = data['ab'].to(self.device)
def forward(self):
self.fake_color = self.net_G(self.L)
def backward_D(self):
fake_image = torch.cat([self.L, self.fake_color], dim=1)
fake_preds = self.net_D(fake_image.detach())
self.loss_D_fake = self.GANcriterion(fake_preds, False)
real_image = torch.cat([self.L, self.ab], dim=1)
real_preds = self.net_D(real_image)
self.loss_D_real = self.GANcriterion(real_preds, True)
self.loss_D = (self.loss_D_fake + self.loss_D_real) * 0.5
self.loss_D.backward()
def backward_G(self):
fake_image = torch.cat([self.L, self.fake_color], dim=1)
fake_preds = self.net_D(fake_image)
self.loss_G_GAN = self.GANcriterion(fake_preds, True)
self.loss_G_L1 = self.L1criterion(self.fake_color, self.ab) * self.lambda_L1
self.loss_G = self.loss_G_GAN + self.loss_G_L1
self.loss_G.backward()
def optimize(self):
self.forward()
self.net_D.train()
self.set_requires_grad(self.net_D, True)
self.opt_D.zero_grad()
self.backward_D()
self.opt_D.step()
self.net_G.train()
self.set_requires_grad(self.net_D, False)
self.opt_G.zero_grad()
self.backward_G()
self.opt_G.step()These functions were nor included in the explanations of the TDS article. These are just some utility functions to log the losses of our network and also visualize the results during training. So here you can check them out:
class AverageMeter:
def __init__(self):
self.reset()
def reset(self):
self.count, self.avg, self.sum = [0.] * 3
def update(self, val, count=1):
self.count += count
self.sum += count * val
self.avg = self.sum / self.count
def create_loss_meters():
loss_D_fake = AverageMeter()
loss_D_real = AverageMeter()
loss_D = AverageMeter()
loss_G_GAN = AverageMeter()
loss_G_L1 = AverageMeter()
loss_G = AverageMeter()
return {'loss_D_fake': loss_D_fake,
'loss_D_real': loss_D_real,
'loss_D': loss_D,
'loss_G_GAN': loss_G_GAN,
'loss_G_L1': loss_G_L1,
'loss_G': loss_G}
def update_losses(model, loss_meter_dict, count):
for loss_name, loss_meter in loss_meter_dict.items():
loss = getattr(model, loss_name)
loss_meter.update(loss.item(), count=count)
def lab_to_rgb(L, ab):
"""
Takes a batch of images
"""
L = (L + 1.) * 50.
ab = ab * 110.
Lab = torch.cat([L, ab], dim=1).permute(0, 2, 3, 1).cpu().numpy()
rgb_imgs = []
for img in Lab:
img_rgb = lab2rgb(img)
rgb_imgs.append(img_rgb)
return np.stack(rgb_imgs, axis=0)
def visualize(model, data, save=True):
model.net_G.eval()
with torch.no_grad():
model.setup_input(data)
model.forward()
model.net_G.train()
fake_color = model.fake_color.detach()
real_color = model.ab
L = model.L
fake_imgs = lab_to_rgb(L, fake_color)
real_imgs = lab_to_rgb(L, real_color)
fig = plt.figure(figsize=(15, 8))
for i in range(5):
ax = plt.subplot(3, 5, i + 1)
ax.imshow(L[i][0].cpu(), cmap='gray')
ax.axis("off")
ax = plt.subplot(3, 5, i + 1 + 5)
ax.imshow(fake_imgs[i])
ax.axis("off")
ax = plt.subplot(3, 5, i + 1 + 10)
ax.imshow(real_imgs[i])
ax.axis("off")
plt.show()
if save:
fig.savefig(f"colorization_{time.time()}.png")
def log_results(loss_meter_dict):
for loss_name, loss_meter in loss_meter_dict.items():
print(f"{loss_name}: {loss_meter.avg:.5f}")I hope this code is self-explanatory. Every epoch takes about 4 minutes on not a powerful GPU as Nvidia P5000. So if you are using 1080Ti or higher, it will be much faster.
def train_model(model, train_dl, epochs, display_every=200):
data = next(iter(val_dl)) # getting a batch for visualizing the model output after fixed intrvals
for e in range(epochs):
loss_meter_dict = create_loss_meters() # function returing a dictionary of objects to
i = 0 # log the losses of the complete network
for data in tqdm(train_dl):
model.setup_input(data)
model.optimize()
update_losses(model, loss_meter_dict, count=data['L'].size(0)) # function updating the log objects
i += 1
if i % display_every == 0:
print(f"\nEpoch {e+1}/{epochs}")
print(f"Iteration {i}/{len(train_dl)}")
log_results(loss_meter_dict) # function to print out the losses
visualize(model, data, save=False) # function displaying the model's outputs
model = MainModel()
train_model(model, train_dl, 100)Every epoch takes about 3 to 4 minutes on Colab. After about 20 epochs you should see some reasonable results.
Okay. I let the model train for some longer (about 100 epochs). Here are the results of our baseline model:
As you can see, although this baseline model has some basic understanding of some most common objects in images like sky, trees, … its output is far from something appealing and it cannot decide on the color of rare objects. It also displays some color spillovers and circle-shaped mass of color (center of first image of second row) which is not good at all. So, it seems like that with this small dataset we cannot get good results with this strategy. Therefore, we change our strategy!
Here is the focus of this article and where I'm going to explain what I did to overcome the last mentioned problem. Inspired by an idea in Super Resolution literature, I decided to pretrain the generator separately in a supervised and deterministic manner to avoid the problem of "the blind leading the blind" in the GAN game where neither generator nor discriminator knows anything about the task at the beginning of training.
Actually I use pretraining in two stages: 1- The backbone of the generator (the down sampling path) is a pretrained model for classification (on ImageNet) 2- The whole generator will be pretrained on the task of colorization with L1 loss.
In fact, I'm going to use a pretrained ResNet18 as the backbone of my U-Net and to accomplish the second stage of pretraining, we are going to train the U-Net on our training set with only L1 Loss. Then we will move to the combined adversarial and L1 loss, as we did in the previous section.
Building a U-Net with a ResNet backbone is not something trivial so I'll use fastai library's Dynamic U-Net module to easily build one. You can simply install fastai with pip or conda. Here's the link to the documentation.
You need to install fastai version 2.4 for the following lines code to run w/o errors.
# pip install fastai==2.4
from fastai.vision.learner import create_body
from torchvision.models.resnet import resnet18
from fastai.vision.models.unet import DynamicUnetdef build_res_unet(n_input=1, n_output=2, size=256):
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
body = create_body(resnet18, pretrained=True, n_in=n_input, cut=-2)
net_G = DynamicUnet(body, n_output, (size, size)).to(device)
return net_GThat's it! With just these few lines of code you can build such a complex model easily. create_body function loads the pretrained weights of the ResNet18 architecture and cuts the model to remove the last two layers (GlobalAveragePooling and a Linear layer for the ImageNet classification task). Then, DynamicUnet uses this backbone to build a U-Net with the needed output channels (2 in our case) and with an input size of 256.
def pretrain_generator(net_G, train_dl, opt, criterion, epochs):
for e in range(epochs):
loss_meter = AverageMeter()
for data in tqdm(train_dl):
L, ab = data['L'].to(device), data['ab'].to(device)
preds = net_G(L)
loss = criterion(preds, ab)
opt.zero_grad()
loss.backward()
opt.step()
loss_meter.update(loss.item(), L.size(0))
print(f"Epoch {e + 1}/{epochs}")
print(f"L1 Loss: {loss_meter.avg:.5f}")
net_G = build_res_unet(n_input=1, n_output=2, size=256)
opt = optim.Adam(net_G.parameters(), lr=1e-4)
criterion = nn.L1Loss()
pretrain_generator(net_G, train_dl, opt, criterion, 20)
#torch.save(net_G.state_dict(), "res18-unet.pt")With this simple function, we pretrain the generator for 20 epochs and then we save its weights. This will take about one hour on Colab. In the following section, we will use this model as the generator for our GAN and train the whole network as before:
net_G = build_res_unet(n_input=1, n_output=2, size=256)
net_G.load_state_dict(torch.load("res18-unet.pt", map_location=device))
model = MainModel(net_G=net_G)
train_model(model, train_dl, 20)Here I'm first loading the saved weights for the generator and then I'm using this model as the generator in our MainModel class which prevents it from randomly initializing the generator. Then we train the model for 10 to 20 epochs! (compare it to the 100 epochs of the previous section when we didn't use pretraining). Each epoch will take about 3 to 4 minutes on Colab which is really great!
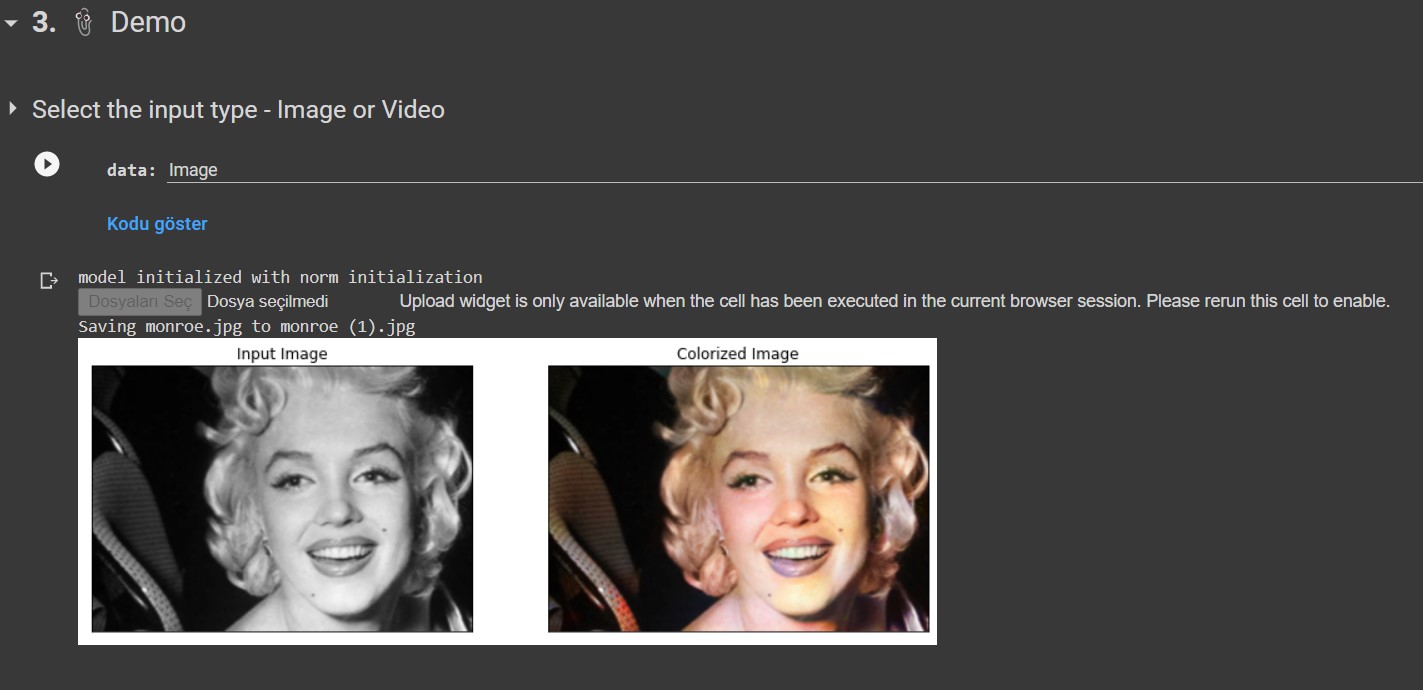
you can refer to the images at the beginning of this tutorial to see the final outputs of this model.
Remember that when I was explaining the theory of conditional GAN in the beginning of this article, I said that the source of the noise in the architecture of the generator proposed by authors of the paper was the dropout layers. However, when I investigated the U-Net we built with the help of fastai, I did not find any dropout layers in there! Actually I first trained the final model and got the results and then I investigated the generator and found this out.
So, was the adversarial training useless? If there is no noise, how possibly the generator can have a creative effect on the output? Is it possible that the input grayscale image to the generator plays the role of noise as well? These were my exact questions at the time.
Therefor, I decided to email Dr. Phillip Isola, the first author of the same paper we implemented here, and he kindly answered these questions. According to what he said, this conditional GAN can still work without dropout but the outputs will be more deterministic because of the lack of that noise; however, there is still enough information in that input grayscale image which enables the generator to produce compelling outputs. Actually, I saw this in practice that the adversarial training was helpful indeed. In the next and last section, I'm going to compare the results of the pretrained U-Net with no adversarial training against the final outputs we got with adversarial training.
One of the cool thing I found in my experiments was that the U-Net we built with the ResNet18 backbone is already awesome in colorizing images after pretraining with L1 Loss only (a step before the final adversarial training). But, the model is still conservative and encourages using gray-ish colors when it is not sure about what the object is or what color it should be. However, it performs really awesome for common scenes in the images like sky, tree, grass, etc.
Here I show you the outputs of the U-Net without adversarial training and U-Net with adversarial training to better depict the significant difference that the adversarial training is making in our case:
(Left: pretrained U-Net without adversarial training | Right: pretrained U-Net with adversarial training)
You can also see the GIF below to observe the difference between the images better:
(animation of the last two images to better see the significant difference that adversarial training is making)
This project was full of important lessons for myself. I spent a lot of time during the last month to implement lots of different papers each with different strategies and it took quite a while and after A LOT of failures that I could come up with this method of training. Now you can see that how pretraining the generator significantly helped the model and improved the results.
I also learned that some observations, although at first feeling like a bad mistake of yours, are worth paying attention to and further investigation; like the case of dropout in this project. Thanks to the helpful community of deep learning and AI, you can easily ask experts and get the answer you need and become more confidant in what you were just guessing.
I want to thank the authors of this wonderful paper for their awesome work and also the great GitHub repository of this paper from which I borrowed some of the codes (with modification and simplification). I truly love the community of computer science and AI and all their hard work to improve the field and also make their contributions available to all. I'm happy to be a tiny part of this community.