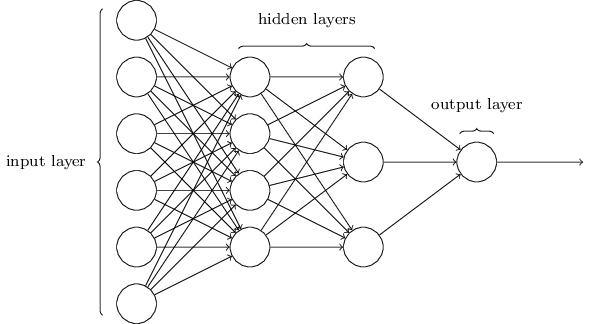
This repository consists the code for a basic neural network, that can be used for the any purpose with a little tweaking it also includes the famous MNSIT dataset with an data expander using the basic process of image alteration.
The Neural Network uses the Quadratic Cost function and Stochastic gradient descent with no regularization.
You should have git installed in your system .
- Fork the repo then In gitbash or terminal if you use mac or linux type: git clone "url of forked repo"
- Start working on the project on the your local machine
- When you're done with the changes add and commit the changes
- Push the project on your forked
- Create a pull request to the orignal project
To check that the Neural network is running without any error run test.py Note: You must have all the basic python libraries installed . Further, the archive handling system needs to be installed on Non Unix and Linux platforms.
The project contains the additional cost functions in the costfunctions.py they can impletmented in the project , further the concepts of Regularization and Data Visualisation and enchancing the performance through little tweaks which will be discussed further are to be implemented.
A neural network is a series of algorithms that endeavors to recognize underlying relationships in a set of data through a process that mimics the way the human brain operates. In this sense, neural networks refer to systems of neurons, either organic or artificial in nature. Neural networks can adapt to changing input; so the network generates the best possible result without needing to redesign the output criteria.
The artificial neural network is like a collection of strings that are ‘tuned’ to training data. Imagine a guitar and the process of tuning its strings to achieve a specific chord. As each string is tightened, it becomes more “in tune” with a specific note, the weight of this tightening causes other strings to require adjustment. Iterating through the strings, each time reducing errors in pitch, and eventually you arrive at a reasonably tuned instrument.
Imagine the weight of each string (synapse) connecting a series of tuning pegs (neurons) and an iterative process to achieve proper tuning (training data). In each iteration there is additional fine tuning (back-propagation) to adjust to the desired pitch. Eventually the instrument is tuned and when played (used for prediction) it will harmonize properly (have acceptably low error rates).
Let’s build a “toy” artificial neural network in software to explore this. The code for our sample is here, we’re using Python . As always we will take a “no black box” approach so we can understand exactly how this machinery works. We’re going to provide a very simple training dataset, a series of 3 binary values and an output: input [ 0, 0, 1 ] output: 0 input [ 1, 1, 1 ] output: 1 input [ 1, 0, 1 ] output: 1 input [ 0, 1, 0] output: 0 Notice that the output seems tied to the first value, that’s the pattern. We don’t know what the output for [ 1, 1, 0] is, for example, but the pattern of the training data suggests strongly that it’s 1.
To know more you can watch this 3b1b series
If you want to dive much in detail you can read this paper
Hey, I'm Dantraz if you like this project and would like to work on it, you've a really great opportunity. To start working on the project as an contestant , join link , you can start of by saying Hi..