Algorithm Studies from my Master's in Computer Science. My degree is from the Georgia Institute of Technology.
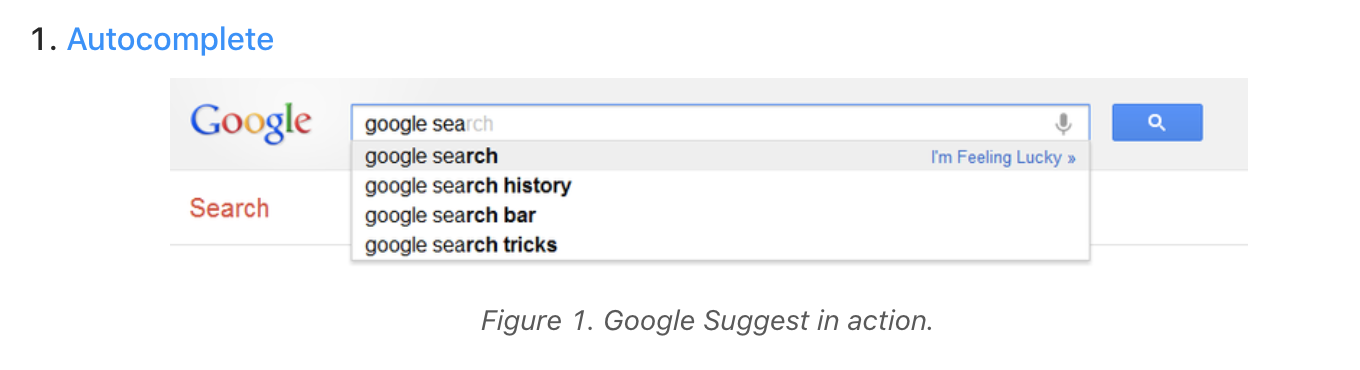
The Trie or prefix tree is a tree data structure we use for retrieval of a key in a dataset of strings. There are various applications of this very efficient data structure such as:
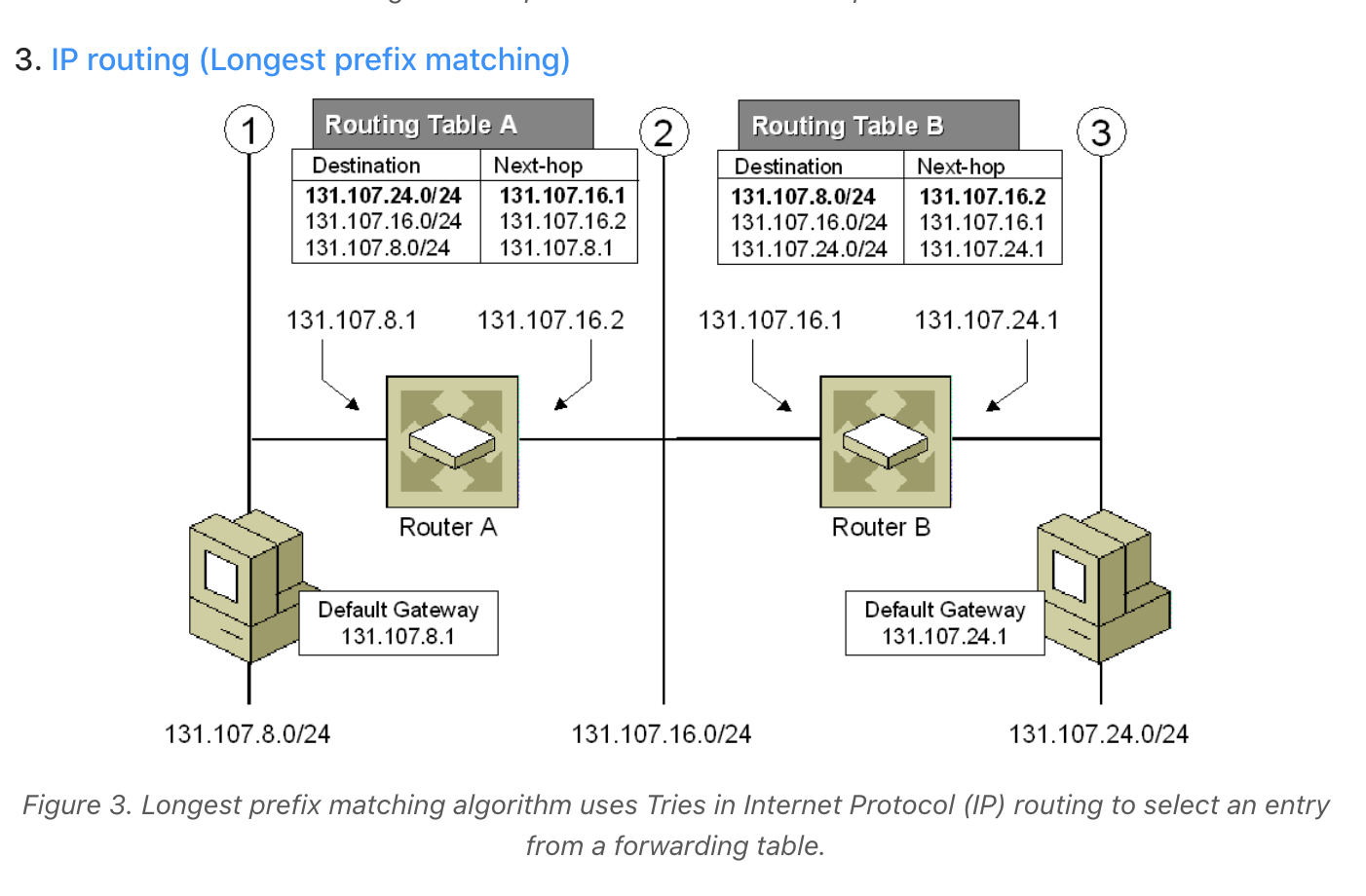
This example is especially interesting due to its relevance in computer networking. The longest prefix matching algorithm is used by routers in Internet Protocol (IP) networking to select an entry from a forwarding table. Because each entry in a forwarding table may specify a sub-network, one destination address may match more than one forwarding table entry. The most specific of the matching table entries -- the one with the longest subnet mask -- is called the longest prefix match. It is called this because it is also the entry where the largest number of leading address bits of the destination address match those in the table entry.
An example IPv4 forwarding table:
192.168.20.16/28
192.168.0.0/16
Suppose the address 192.168.20.19 needs to be looked up. Both of
these entries in the forwarding table "match", meaning both
entries contain the looked up address. The longest prefix of these
two candidate routes is 192.168.20.16/28 because its subnet mask
(/28) is longer than the other entry's mask (/16), making the
router more specific.
Other data structures, like balanced trees and hash tables, also give us the ability to search for a word in a dataset of strings. So why a trie? Even though a hash table has O(1) time complexity for looking for a key, it is not efficient in the following operations:
- Finding all keys with a common prefix
- Enumerating a dataset of strings in lexicographical order
Furthermore, as a hash table increases in size, there are lots of hash collisions, and the search time complexity could deteriorate to O(N), where N is the number of keys inserted. A trie could use less space compared to a Hash Table when storing many keys with the same prefix. In this case, employing a trie has only O(M) time complexity, where M is the key length. Also, searching for a key in a balanced tree costs O(M log M) time.
A trie is a rooted tree, and its nodes have the following fields
- Maximum of R links to its children where each link corresponds to one of R character values from the dataset of an alphabet. Assume R == 26, the number of lowercase latin letters.
- Boolean field which specifies whether the node corresponds to the end of the key or is just a prefix.
class TrieNode {
// R links to node children
private TrieNode[] links;
private final int R = 26;
private boolean isEnd;
public TrieNode() {
links = new TrieNode[R];
}
public boolean containsKey(char ch) {
return links[ch -'a'] != null;
}
public TrieNode get(char ch) {
return links[ch -'a'];
}
public void put(char ch, TrieNode node) {
links[ch -'a'] = node;
}
public void setEnd() {
isEnd = true;
}
public boolean isEnd() {
return isEnd;
}
}Two of the most common operations in a trie are insertion of a key and search for a key.
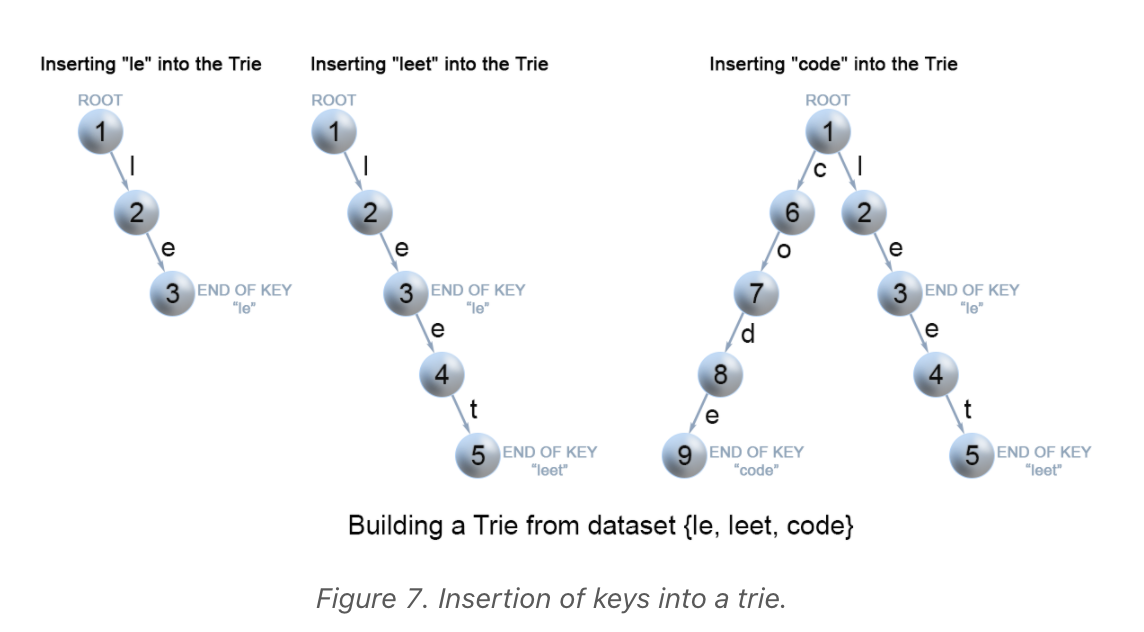
We insert a key by searching into the trie. First, we visit the root and search a link. which corresponds to the first key character. Two cases will ensue:
- A link exists; therefore, move down the tree following the link to the next child level. The algorithm continues with searching for the next key character.
- A link does not exist. We will now create a new node and link it with the parent's link matching the current key character. This step will be repeated until we encounter the last character of the key. At that point, we mark the current node as an end node and the algorithm completes.
class Trie {
private TrieNode root;
public Trie() {
root = new TrieNode();
}
// Inserts a word into the trie.
public void insert(String word) {
TrieNode node = root;
for (int i = 0; i < word.length(); i++) {
char currentChar = word.charAt(i);
if (!node.containsKey(currentChar)) {
node.put(currentChar, new TrieNode());
}
node = node.get(currentChar);
}
node.setEnd();
}
}-
Time Complexity: O(M) where M is the key length During each iteration of the algorithm, we are either creating or examining a node in the trie until we reach the end of the key. This takes only M operations.
-
Space complexity: O(M) In the worst case, the newly inserted key does not share a prefix with the keys already inserted in the trie. We will then have to add M new nodes, which will takes us O(M) space.
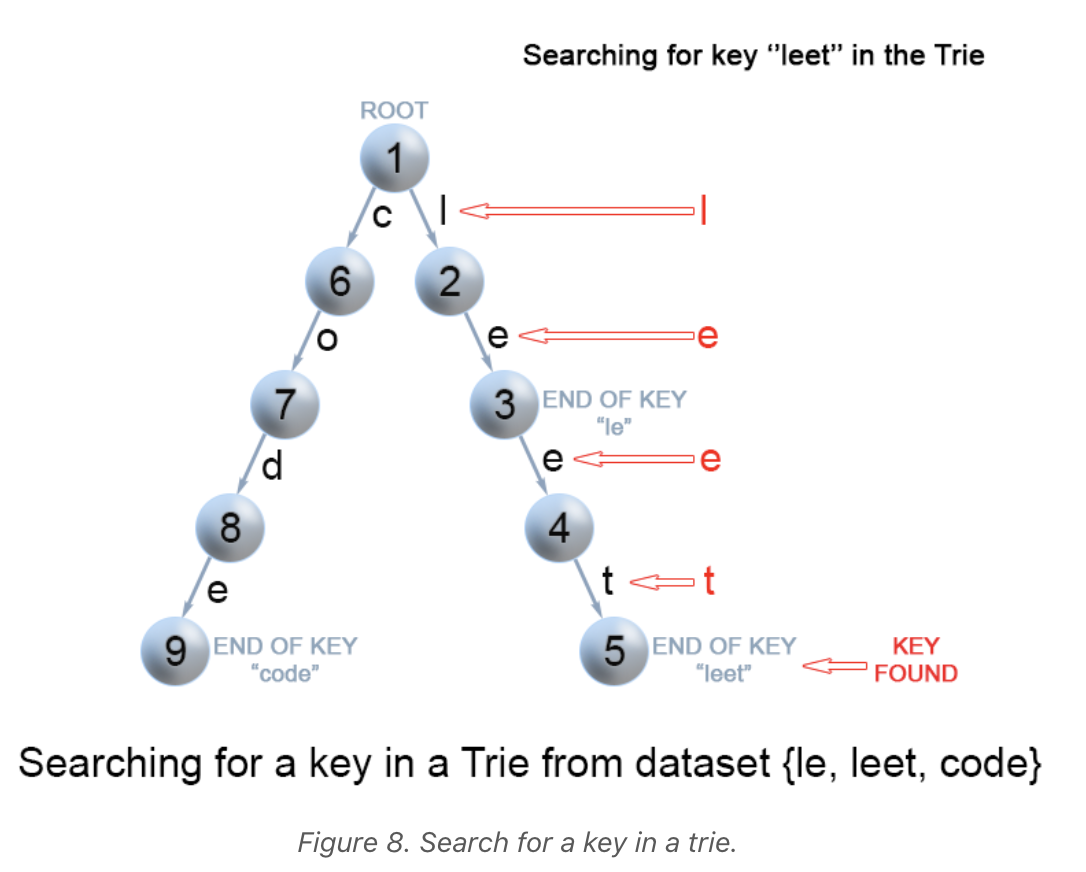
Each key is represented in the trie as a path from the root to the internal node or leaf. We start from the root with the first key character, then we examine the current node for a link corresponding to a key character. There are two cases when searching:
- A link exists; we move to the next node in the path following this link, and proceed searching for the next key character.
- A link does not exist; if there are no available key characters
and the current node is marked as
isEnd, we return true. Otherwise, there are two more possible cases where we return false:- There are key characters left, but it is impossible to follow the key path in the trie, and the key is missing.
- No key characters are left, but the current node is not marked as isEnd. Therefore, the search key is only a prefix of another key in the trie.
class Trie {
...
// search a prefix or whole key in trie and
// returns the node where search ends
private TrieNode searchPrefix(String word) {
TrieNode node = root;
for (int i = 0; i < word.length(); i++) {
char curLetter = word.charAt(i);
if (node.containsKey(curLetter)) {
node = node.get(curLetter);
} else {
return null;
}
}
return node;
}
// Returns if the word is in the trie.
public boolean search(String word) {
TrieNode node = searchPrefix(word);
return node != null && node.isEnd();
}
}- Time Complexity: O(M) - In each step of the algorithm, we search for the next key character. In the worst case, the algorithm performs M operations.
- Space Complexity: O(1)
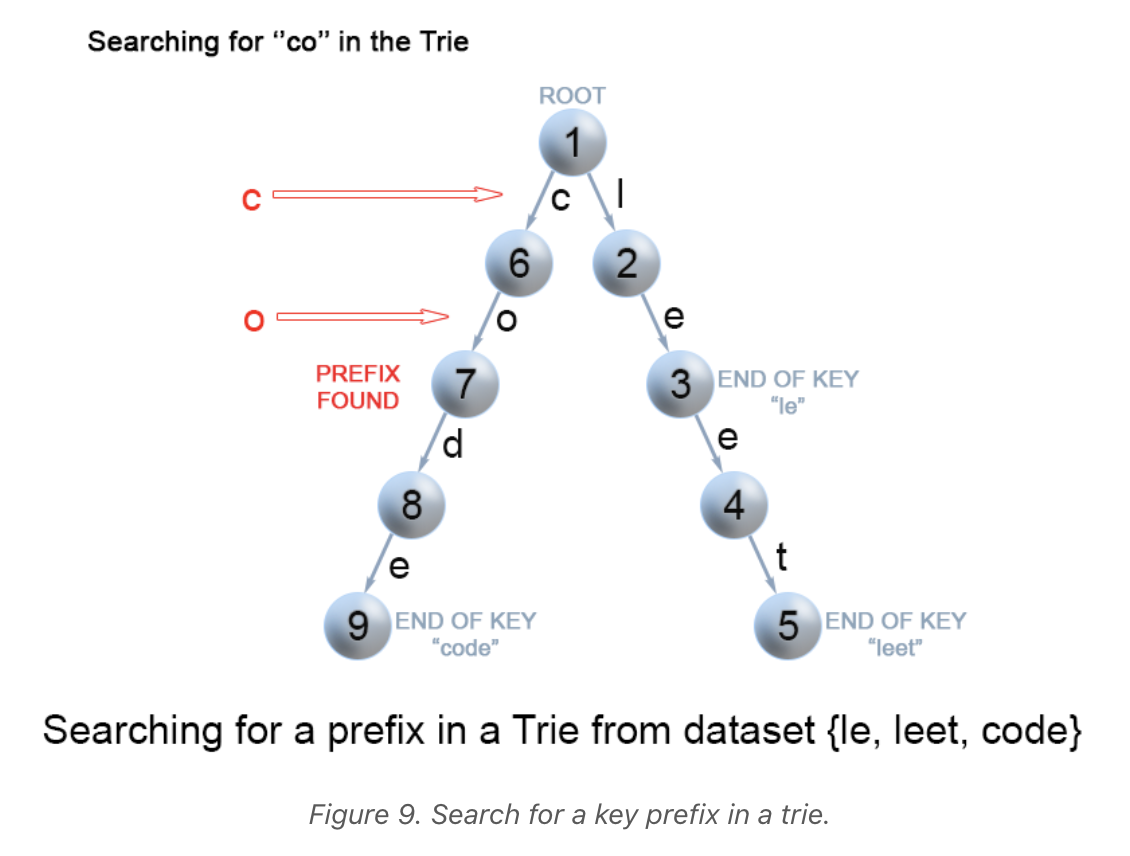
Similar to searching a key in a trie, we traverse the trie from
the root until there are no characters left in the key prefix or
it is impossible to continue the path in the trie with the current
key character. The only difference is that when we come to an end of
the key prefix, we always return true. We do not need to consider
the boolean isEnd because we are searching for a prefix of a key,
not a whole key.
class Trie {
...
// Returns if there is any word in the trie
// that starts with the given prefix.
public boolean startsWith(String prefix) {
TrieNode node = searchPrefix(prefix);
return node != null;
}
}- Time Complexity: O(M)
- Space Complexity: O(1)
For a certain Georgia Tech project in which we were tasked to consider all permutations of an input, I found the algorithm to generate these test cases quite clever. Through my studies, I discovered the approach of backtracking.
Backtracking is an algorithm for finding all solutions by exploring all potential candidates. If the solution candidate turns out to not be a solution, then the algorithm will discard it by making some changes on the previous step. These changes on the previous step are the backtracking idea to this algorithmic approach.
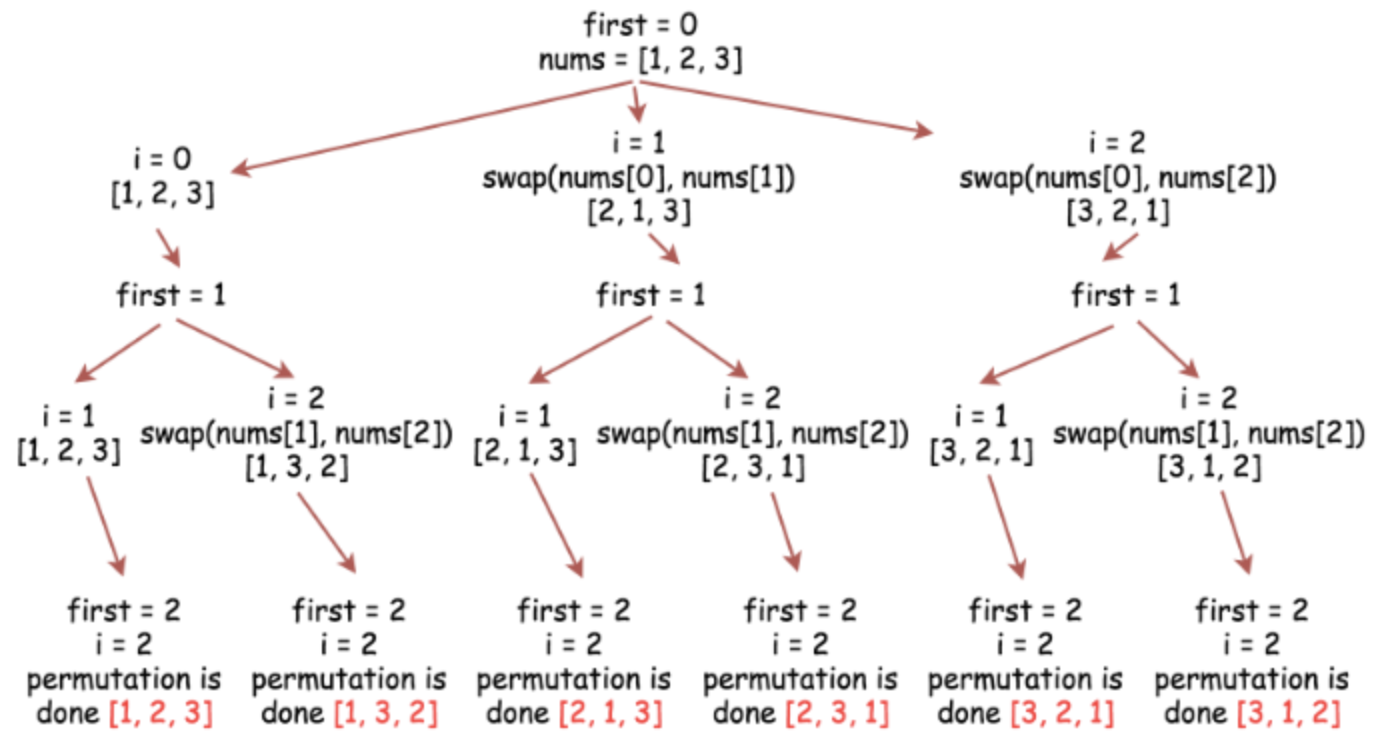
Imagine the problem space where you are given a distinct integer array and must create all possible permutations of this array. An example of such an array is [1,2,3]. A backtrack function that takes the index of the first integer to consider as an argument would work as follows:
- If the first integer to consider has index
n, that means that the current permutation is done. - Iterate over the integers from index
firstto indexn-1.- Place the
i-th integer first in the permutation, i.e.swap(nums[first], nums[i]) - Proceed to create all permutations which start from the
i-th integer:backtrack(first + 1) - Now, backtrack, i.e.
swap(nums[first], nums[i])back
- Place the
Imagine this problem space: Given a circular array C of integers represented by A, find the maximum possible sum of a non-empty subarray of C.
Here, a circular array means the end of the array connects to the beginning of the array. (Formally, C[i] = A[i] when 0 <= i < A.length, and C[i+A.length] = C[i] when i >= 0.)
Also, a subarray may only include each element of the fixed buffer A at most once. (Formally, for a subarray C[i], C[i+1], ..., C[j], there does not exist i <= k1, k2 <= j with k1 % A.length = k2 % A.length.)
Example 1:
Input: [1,-2,3,-2]
Output: 3
Explanation: Subarray [3] has maximum sum 3
Example 2:
Input: [5,-3,5]
Output: 10
Explanation: Subarray [5,5] has maximum sum 5 + 5 = 10
Example 3:
Input: [3,-1,2,-1]
Output: 4
Explanation: Subarray [2,-1,3] has maximum sum 2 + (-1) + 3 = 4
Example 4:
Input: [3,-2,2,-3]
Output: 3
Explanation: Subarray [3] and [3,-2,2] both have maximum sum 3
Example 5:
Input: [-2,-3,-1]
Output: -1
Explanation: Subarray [-1] has maximum sum -1
To understand the solutions for this problem, I found it best to
explore Kadane's algorithm. The algorithm can be used to find the
maximum sum of the subarrays of an array A. The algorithm is
based on dynamic programming. Let dp[j] be the maximum sum of a
subarray that ends in A[j]. For example, dp[j] = max(A[i] + A[i+1] + ... + A[j])
Therefore, a sum ending in j+1 maximized the A[i] + ... + A[j] part
of the sum by being equal to dp[j] if it is non-empty, and 0 if
it is.
dp[j+1] = A[j+1] + max(dp[j],0). The maximum element of dp[j] will
be the desired answer here.
Now, how do we compute dp efficiently? We will maintain two variables
to reduce space complexity: ans as the max(dp[j]) and cur as the
current dp[j] we are computing. We update these variables as j iterates
from 0 to A.length - 1.
The following pseudocode explains the approach well:
#Kadane's algorithm
ans = cur = None
for x in A:
cur = x + max(cur, 0)
ans = max(ans, cur)
return ans
Subarrays of circular arrays can be classified as either a one-interval subarray or a two-interval subarray. For example, if A = [0, 1, 2, 3, 4, 5, 6] is the underlying buffer of our circular array, we could represent the subarray [2, 3, 4] as one interval [2,4], but we would represent the subarray [5, 6, 0, 1] as two intervals [5,6],[0,1].
Via Kidane's algorithm, we know how to get the maximum of one-interval subarrays, so it only remains to consider two-interval subarrays. The code looks like the following:
class Solution {
public int maxSubarraySumCircular(int[] A) {
int N = A.length;
int ans = A[0], cur = A[0];
for (int i = 1; i < N; ++i) {
cur = A[i] + Math.max(cur, 0);
ans = Math.max(ans, cur);
}
// ans is the answer for 1-interval subarrays.
// Now, let's consider all 2-interval subarrays.
// For each i, we want to know
// the maximum of sum(A[j:]) with j >= i+2
// rightsums[i] = A[i] + A[i+1] + ... + A[N-1]
int[] rightsums = new int[N];
rightsums[N-1] = A[N-1];
for (int i = N-2; i >= 0; --i)
rightsums[i] = rightsums[i+1] + A[i];
// maxright[i] = max_{j >= i} rightsums[j]
int[] maxright = new int[N];
maxright[N-1] = A[N-1];
for (int i = N-2; i >= 0; --i)
maxright[i] = Math.max(maxright[i+1], rightsums[i]);
int leftsum = 0;
for (int i = 0; i < N-2; ++i) {
leftsum += A[i];
ans = Math.max(ans, leftsum + maxright[i+2]);
}
return ans;
}
}Imagine you are given an interface that holds a secret word. You are given a list of unique words, which are all 6 letters long. One word in this list is the secret word. You can call this interface to make guesses at what the secret word is. You only have 10 guesses to guess the word. An example is below:
Example 1:
Input: secret = "acckzz", wordlist = ["acckzz","ccbazz","eiowzz","abcczz"]
Explanation:
master.guess("aaaaaa") returns -1, because "aaaaaa" is not in wordlist.
master.guess("acckzz") returns 6, because "acckzz" is secret and has all 6 matches.
master.guess("ccbazz") returns 3, because "ccbazz" has 3 matches.
master.guess("eiowzz") returns 2, because "eiowzz" has 2 matches.
master.guess("abcczz") returns 4, because "abcczz" has 4 matches.
We made 5 calls to master.guess and one of them was the secret, so we pass the test case.
There are 5 additional test cases with 100 words each in the given word list.
The less words in this unique words list, the better. It will be easier to deduce teh secret word if we are given less words to choose from. Therefore, how do we make educated guesses; that is, how do we make guesses that minimize the resulting word list we should then choose from?
Thinking more deeply about this problem, we can recognize that there is no solution that can guarantee to find a secret word in 10 tries. For instance, if the test case was ["aaaaaa", "bbbbbb", ..., "zzzzzz"], then we would need 26 tries to find the secret in the worst case. Therefore, we are really just being tested on a smart strategy.
We take a word from the unique word list and guess. Next, update the wordlist to keep only the same matches to our guess. A matching helper function could be the following:
public int match(String a, String b) {
int matches = 0;
for (int i = 0; i < a.length(); ++i)
if (a.charAt(i) == b.charAt(i))
matches ++;
return matches;
}We could have a random approach since all of the words are generated randomly. Let's just generate a word of length six that is random and test it.
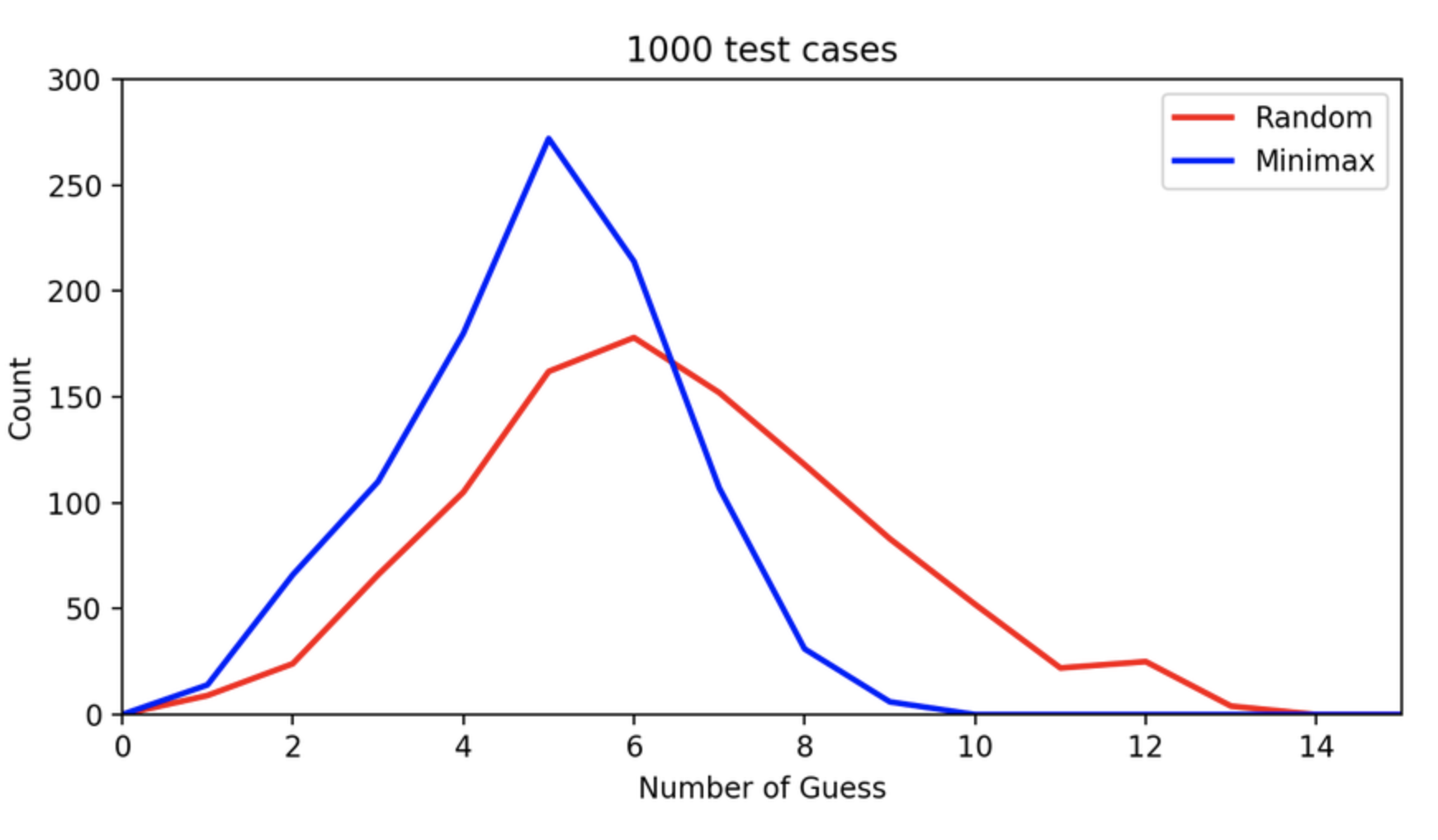
Is it easy to get a good match? The possibility to get 0 matches with the secret word is (25/26)6 = 79.03%. This high probability of getting 0 matches means that the size of the unique wordlist will reduce slowly! Let's try and find candidates that have a large "family", that is the fewest 0 matched with other words. For each word, we note how many words of 0 matches it gets. Then, we guess the word with the minimum words of 0 matches.
With these two approaches in mind, here are the results with 1000 testcases: