meshpro/meshplex

:spider_web: Compute interesting points, areas, and volumes in simplex meshes of any dimension.

Fast tools for simplex meshes.

Compute all sorts of interesting points, areas, and volumes in simplex (triangle, tetrahedral, n-simplex) meshes of any dimension, with a focus on efficiency. Useful in many contexts, e.g., finite-element and finite-volume computations.

Installation

Install meshplex from PyPI with

pip install meshplex

For full usage of meshplex, you require a license. Licenses for personal and academic use can be purchased here. For more info, see here.

Quickstart

meshplex can compute the following data:

import meshplex

# create a simple Mesh instance
points = [[0.0, 0.0], [1.0, 0.0], [0.0, 1.0]]
cells = [[0, 1, 2]]
mesh = meshplex.Mesh(points, cells)
# or read it from a file
# mesh = meshplex.read("pacman.vtk")

# triangle volumes, heights
print(mesh.cell_volumes)
print(mesh.signed_cell_volumes)
print(mesh.cell_heights)

# circumcenters, centroids, incenters
print(mesh.cell_circumcenters)
print(mesh.cell_centroids)
print(mesh.cell_incenters)

# circumradius, inradius, cell quality
print(mesh.cell_circumradius)
print(mesh.cell_inradius)
print(mesh.q_radius_ratio)  # d * inradius / circumradius (min 0, max 1)

# control volumes, centroids
print(mesh.control_volumes)
print(mesh.control_volume_centroids)

# covolume/edge length ratios
print(mesh.ce_ratios)

# count Delaunay violations
print(mesh.num_delaunay_violations)

# removes some cells
mesh.remove_cells([0])

For triangular meshes (MeshTri), meshplex also has some mesh manipulation routines:

mesh.show()  # show the mesh
mesh.angles  # compute angles
mesh.flip_until_delaunay()  # flips edges until the mesh is Delaunay

For a documentation of all classes and functions, see readthedocs.

(For mesh creation, check out this list).

Plotting

Triangles

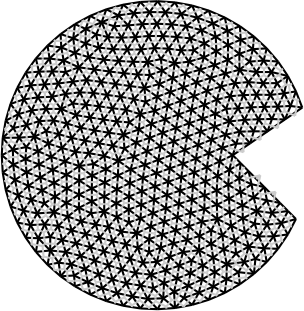
import meshplex

mesh = meshplex.read("pacman.vtk")
mesh.show(
    # show_coedges=True,
    # control_volume_centroid_color=None,
    # mesh_color="k",
    # nondelaunay_edge_color=None,
    # boundary_edge_color=None,
    # comesh_color=(0.8, 0.8, 0.8),
    show_axes=False,
)

Tetrahedra

import numpy as np
import meshplex

# Generate tetrahedron
points = np.array(
    [
        [1.0, 0.0, -1.0 / np.sqrt(8)],
        [-0.5, +np.sqrt(3.0) / 2.0, -1.0 / np.sqrt(8)],
        [-0.5, -np.sqrt(3.0) / 2.0, -1.0 / np.sqrt(8)],
        [0.0, 0.0, np.sqrt(2.0) - 1.0 / np.sqrt(8)],
    ]
) / np.sqrt(3.0)
cells = [[0, 1, 2, 3]]

# Create mesh object
mesh = meshplex.MeshTetra(points, cells)

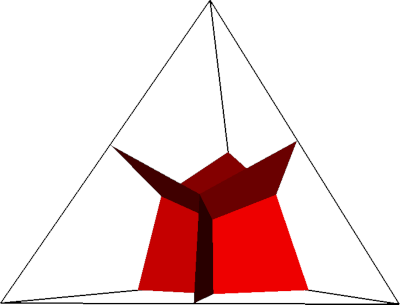
# Plot cell 0 with control volume boundaries
mesh.show_cell(
    0,
    # barycenter_rgba=(1, 0, 0, 1.0),
    # circumcenter_rgba=(0.1, 0.1, 0.1, 1.0),
    # circumsphere_rgba=(0, 1, 0, 1.0),
    # incenter_rgba=(1, 0, 1, 1.0),
    # insphere_rgba=(1, 0, 1, 1.0),
    # face_circumcenter_rgba=(0, 0, 1, 1.0),
    control_volume_boundaries_rgba=(1.0, 0.0, 0.0, 1.0),
    line_width=3.0,
)