Your entry-point for creating & running quantum programs.
This repository holds a wide collection of quantum functions, algorithms, applications and tutorials built with Classiq.
⚛️ Platform | 👋 Join Slack | 📖 Documentation | Getting Started
Working with Classiq's latest GUI requires no installations! Just head over to Classiq's platform and follow the examples below over there :)
If you'd rather work programmatically, using Python, Classiq also provides an SDK, which can be installed as follows:
pip install classiqPlease note that the latest Classiq SDK for Python doesn't work in Python 3.12 yet. Please refer to Issue #17.
This repository has 2 kinds of demos: .qmod and .ipynb.
The .qmod files are intended for usage with Classiq's platform.
Upload those .qmod files into the Synthesis tab
The .ipynb files are intended to be viewed inside JupyterLab.
The simplest quantum circuit has 1 qubit, and has a single X gate.
Using Classiq's SDK, it would like like so:
from classiq import *
NUM_QUBITS = 1
@qfunc
def main(res: Output[QBit]):
allocate(NUM_QUBITS, res)
X(res)
model = create_model(main)
quantum_program = synthesize(model)
show(quantum_program)
result = execute(quantum_program).result()
print(result[0].value.parsed_counts)
# [{'res': 1.0}: 1000]Let's unravel the code above:
def main: We define the logic of our quantum program. We'll expand on this point soon below.create_model: We convert the logic we defined into a Model.synthesize: We synthesize the Model into a Quantum Program. From a logical definition of quantum operations, into a series of quantum gates.execute: Executing the quantum program. Can be executed on a physical quantum computer, or on simulations.
The function above had 4 lines:
@qfunc
def main(res: Output[QBit]):
allocate(NUM_QUBITS, res)
X(res)The 1st line states that the function will be a quantum one. Further documentation.
The 2nd line defines the type of the output. Further examples on types
The 3rd line allocates several qubits (in this example, only 1) in this quantum variable. Further details on allocate
The 4th line applies an X operator on the quantum variable. Further details on quantum operators
Initializing
@qfunc
def prep_minus(out: Output[QBit]) -> None:
allocate(1, out)
X(out)
H(out)A part of the Deutsch Jozsa algorithm (see the full algorithm here)
@qfunc
def deutsch_jozsa(predicate: QCallable[QNum, QBit], x: QNum) -> None:
hadamard_transform(x)
my_oracle(predicate=lambda x, y: predicate(x, y), target=x)
hadamard_transform(x)A part of a QML encoder (see the full algorithm here)
@qfunc
def angle_encoding(exe_params: CArray[CReal], qbv: Output[QArray[QBit]]) -> None:
allocate(exe_params.len, qbv)
repeat(
count=exe_params.len,
iteration=lambda index: RY(pi * exe_params[index], qbv[index]),
)For more, see this repository :)
As we saw above, the main function can be converted to a model using model = create_model(main).
A model is built out of 2 parts: a qmod, and synthesis options.
The former is a quantum language used for defining quantum programs, while the latter is a configuration for the execution of the program.
The model can be saved via write_qmod(model, "file_name"), which will save 2 files: file_name.qmod and file_name.synthesis_options.json.
You may encounter these files in this repository.
This is where the magic happens. Taking a model, which is a set of logical operations, and synthesizing it into physical qubits and the gates entangling them, is not an easy task.
Classiq's synthesis engine is able to optimize this process, whether by requiring the minimal amount of physical qubits, thus reusing as many qubits as possible, or by requiring minimal circuit width, thus lowering execution time and possible errors.
Classiq provides an easy-to-use way to execute quantum programs, and provides various insights of the execution results.
1 diagram is worth a thousand words
flowchart
IDEInput[<a href='https://platform.classiq.io/'>Classiq IDE</a>]
SDKInput[<a href='https://docs.classiq.io/latest/sdk-reference/'>Classiq python SDK</a>]
Model[<a href='https://docs.classiq.io/latest/qmod-reference/'>Quantum Model</a>]
Synthesis[<a href='https://docs.classiq.io/latest/classiq_101/classiq_concepts/optimize/'>Synthesis Engine</a>]
QuantumProgram[Quantum Program]
Execution[<a href='https://docs.classiq.io/latest/classiq_101/classiq_concepts/execute/'>Execution</a>]
Analyze[<a href='https://docs.classiq.io/latest/classiq_101/classiq_concepts/analyze/'>Analyze & Debug</a>]
IBM[IBM]
Amazon[Amazon Braket]
Azure[Azure Quantum]
Nvidia[Nvidia]
IDEInput --> Model;
SDKInput --> Model;
Model --> Synthesis;
Synthesis --> QuantumProgram;
ExternalProgram <--> QuantumProgram;
QuantumProgram --> Analyze;
QuantumProgram --> Execution;
Execution --> IBM
Execution --> Amazon
Execution --> Azure
Execution --> Nvidia
With Classiq, you can build anything. Classiq provides a powerful modeling language to describe any quantum program, which can then be synthesized and executed on any hardware or simulator. Explore our Documentation to learn everything.
from classiq import (
QArray,
Output,
allocate,
qfunc,
X,
QNum,
synthesize,
create_model,
show,
execute,
)
@qfunc
def get_3(x: Output[QArray]) -> None:
allocate(2, x)
X(x[0])
X(x[1])
@qfunc
def get_5(x: Output[QArray]) -> None:
allocate(3, x)
X(x[0])
X(x[2])
@qfunc
def main(res: Output[QNum]) -> None:
a = QNum("a")
b = QNum("b")
get_3(a)
get_5(b)
res |= a + b # should be 8
model = create_model(main)
quantum_program = synthesize(model)
show(quantum_program)
result = execute(quantum_program).result()
print(result[0].value.parsed_counts)The examples found in this repository can be accessed via Classiq's platform, in the model tab, under the same folder structure.
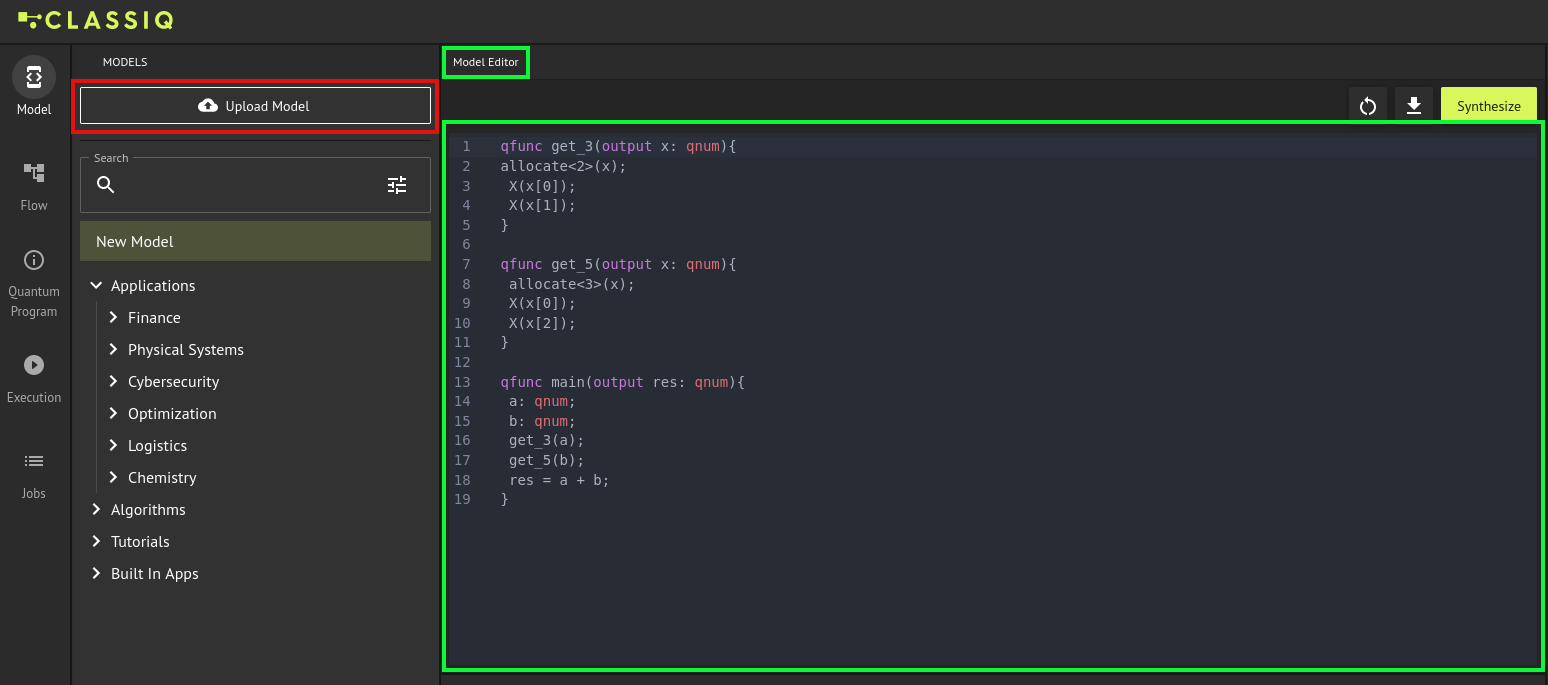
Additionally, one may write his own model in the model editor (highlighted in green) or upload his own model (highlighted in red)
- Create a model (paste in the
modeltab)
qfunc get_3(output x: qnum){
allocate<2>(x);
X(x[0]);
X(x[1]);
}
qfunc get_5(output x: qnum){
allocate<3>(x);
X(x[0]);
X(x[2]);
}
qfunc main(output res: qnum){
a: qnum;
b: qnum;
get_3(a);
get_5(b);
res = a + b;
}
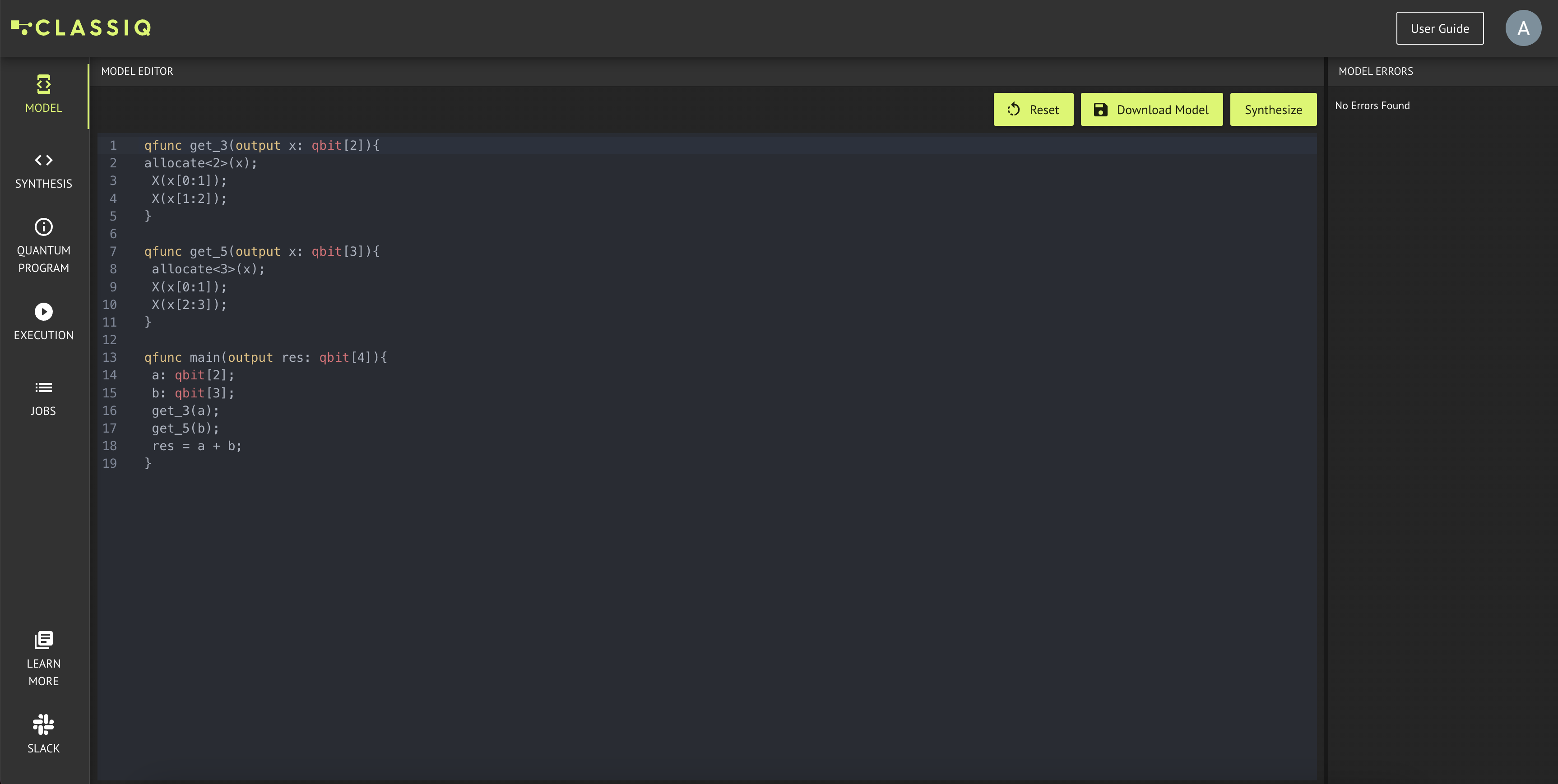
- Press Synthesize:
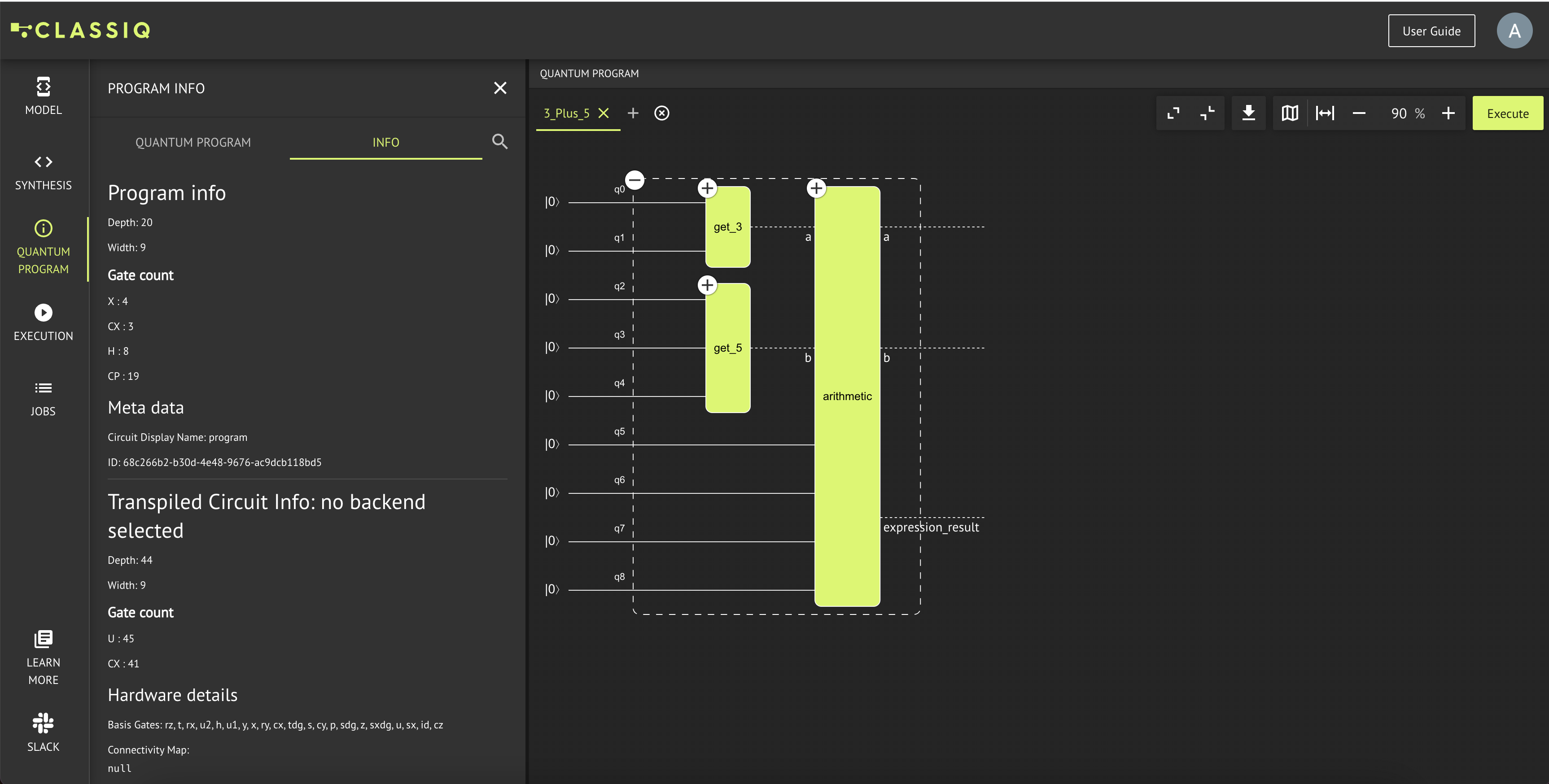
- Press Execute:
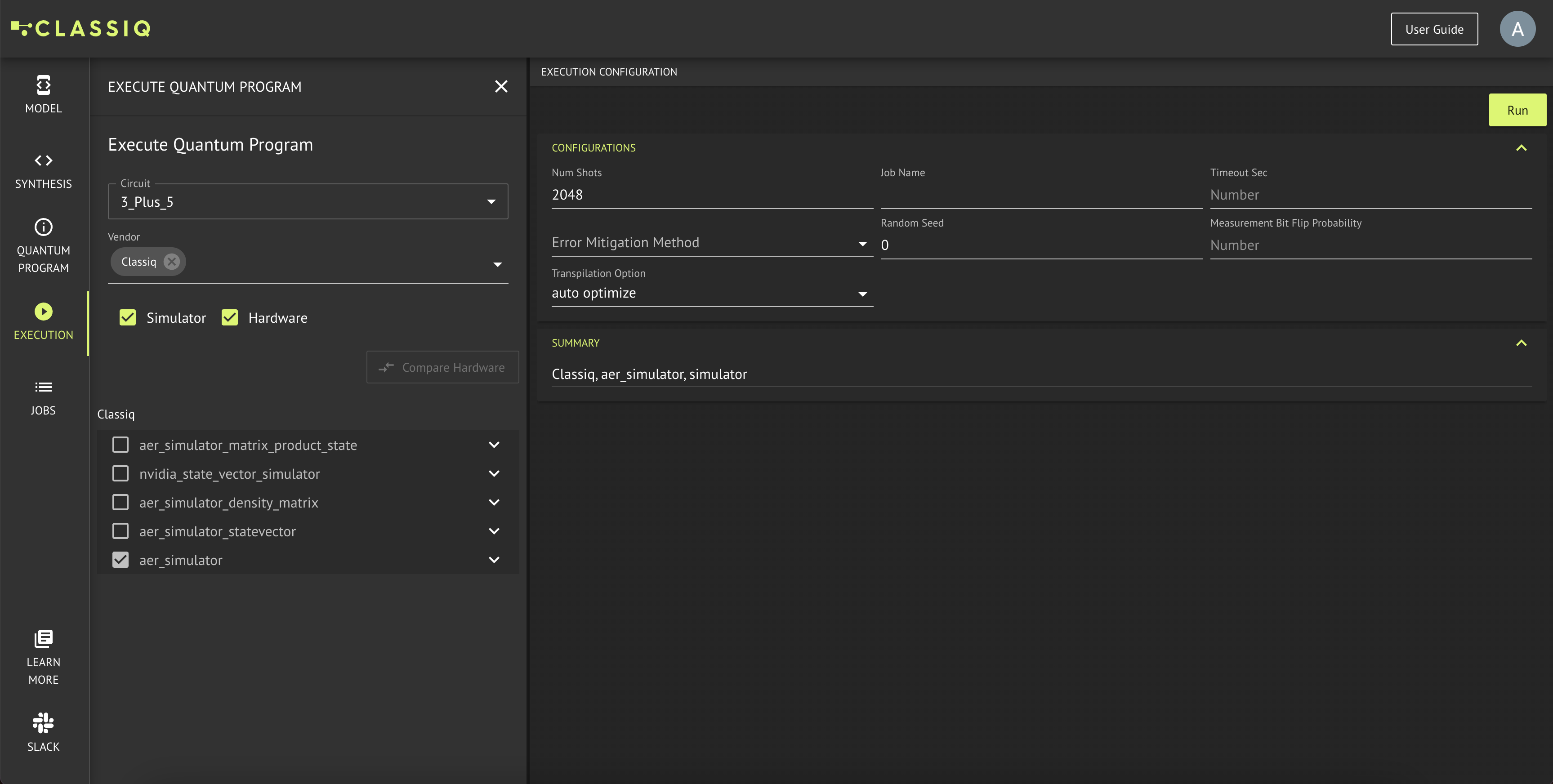
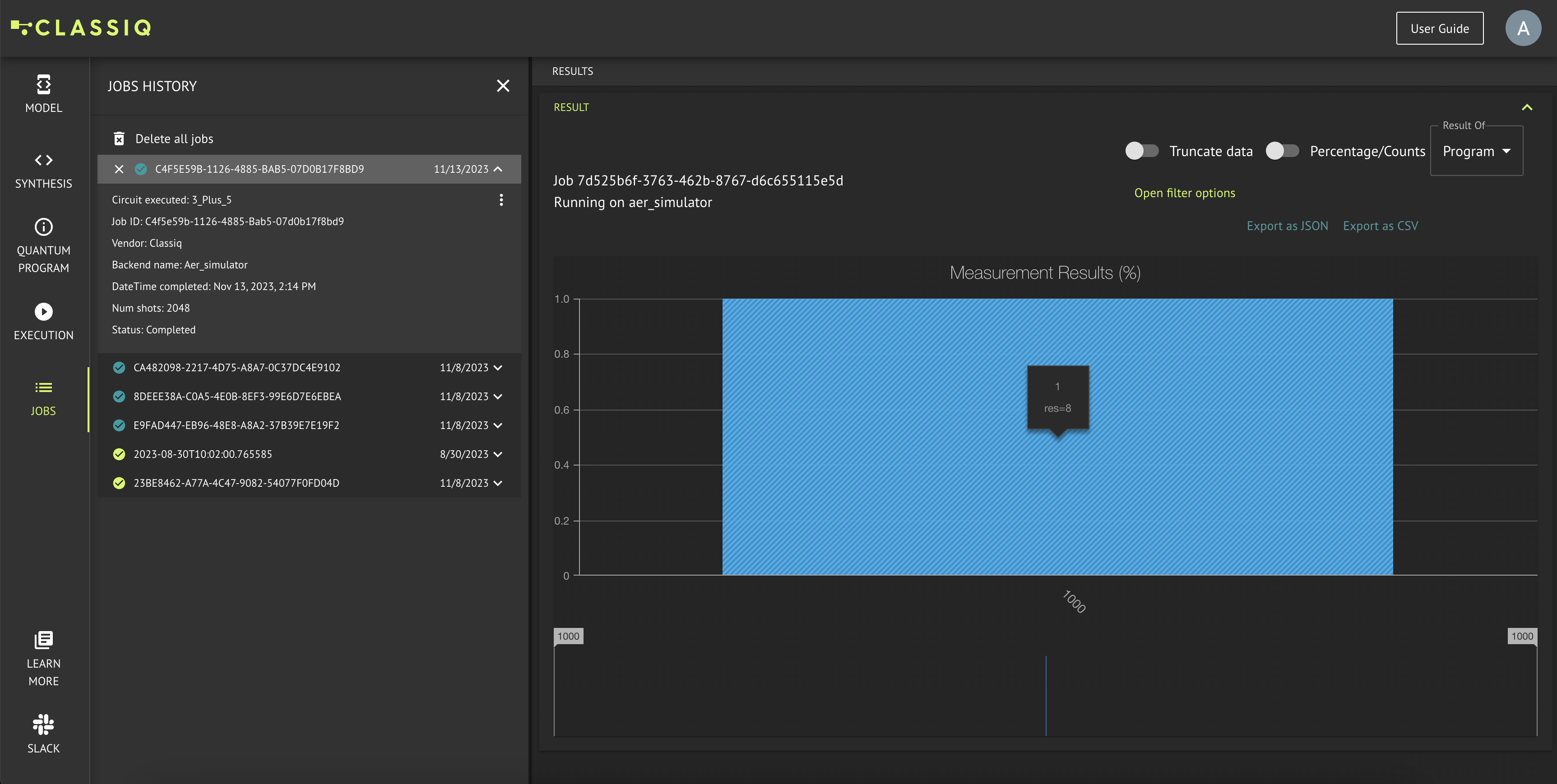
- Press Run:
- View Results:
Have questions? Feedback? Something to share? Welcome to join our open Slack Community