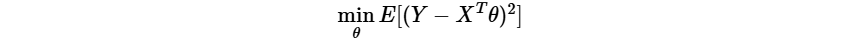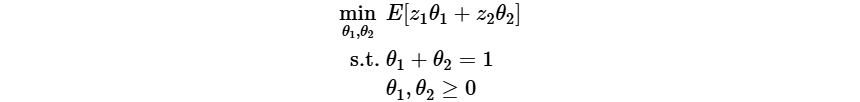This repository contains the Python implementation of the VE (VoteEnsemble) family of ensemble learning methods:
Among the three methods,
1. cd to the root directory, i.e., VoteEnsemble, of this repository.
2. Install the required dependencies, setuptools, numpy and zstandard, if not already intalled. You can install them directly with
pip install setuptools numpy zstandard
or
pip install -r requirements.txt
3. Install VoteEnsemble via
pip install .
To use VoteEnsemble, you need to define a base learning algorithm for you problem by subclassing the BaseLearner class defined in VoteEnsemble.py. Below are two simple use cases to illustrate this.
Consider a linear regression
where exampleLR.py implements such an example, where the base learning algorithm is least squares, and applies
python exampleLR.py
which shall produce the result
True model parameters = [0. 1. 2. 3. 4. 5. 6. 7. 8. 9.]
ROVE outputs the parameters: [3.92431628e-03 1.01457683e+00 1.96402875e+00 3.01047031e+00
4.00479241e+00 5.00741279e+00 5.99596621e+00 7.01602010e+00
7.99180409e+00 8.99286178e+00]
ROVEs outputs the parameters: [-7.11339923e-03 1.00764019e+00 1.97278415e+00 3.00220791e+00
3.99707439e+00 5.02509414e+00 5.98887793e+00 7.02417495e+00
8.01337643e+00 8.96901555e+00]
Consider a simple linear program with random coefficients
where exampleLP.py implements such an example, where the base learning algorithm is the sample average approximation, and applies
python exampleLP.py
which shall produce the result
True optimal objective value = 0.0
MoVE outputs the solution: [1. 0.], objective value = 0.0
ROVE outputs the solution: [1. 0.], objective value = 0.0
ROVEs outputs the solution: [1. 0.], objective value = 0.0
The VE methods involve constructing and evaluating ensembles on many random subsamples of the full dataset, which can be easily parallelized. This implementation supports parallelization through multiprocessing. By default, parallelization is disabled, but you can enable it when creating instances of each method as follows:
# Parallelize ensemble construction in MoVE with 8 processes
move = MoVE(yourBaseLearner, numParallelLearn=8)
# Parallelize ensemble construction and evaluation in ROVE with 8 and 6 processes respectively
rove = ROVE(yourBaseLearner, False, numParallelLearn=8, numParallelEval=6)
# Parallelize ensemble construction and evaluation in ROVEs with 8 and 6 processes respectively
roves = ROVE(yourBaseLearner, True, numParallelLearn=8, numParallelEval=6)
If your machine learning model or optimization solution is memory-intensive, it may not be feasible to store the entire ensemble in RAM. This implementation provides a feature to offload all learned models/solutions to disk, and load a model/solution to memory only when the methods need access to it. By default, this feature is disabled, but you can enable it as follows:
# Offload the ensemble in MoVE to the specified directory
move = MoVE(yourBaseLearner, subsampleResultsDir="path/to/your/directory")
# Offload the ensemble in ROVE to the specified directory
rove = ROVE(yourBaseLearner, False, subsampleResultsDir="path/to/your/directory")
# Offload the ensemble in ROVEs to the specified directory and retain it after execution
roves = ROVE(yourBaseLearner, True, subsampleResultsDir="path/to/your/directory", deleteSubsampleResults=False)