mikepierce/YTYGraphTransforms

Mathematica package for performing triangle-wye (TY) and wye-triangle (YT) transforms

Wye-Triangle-Wye Graph Transforms

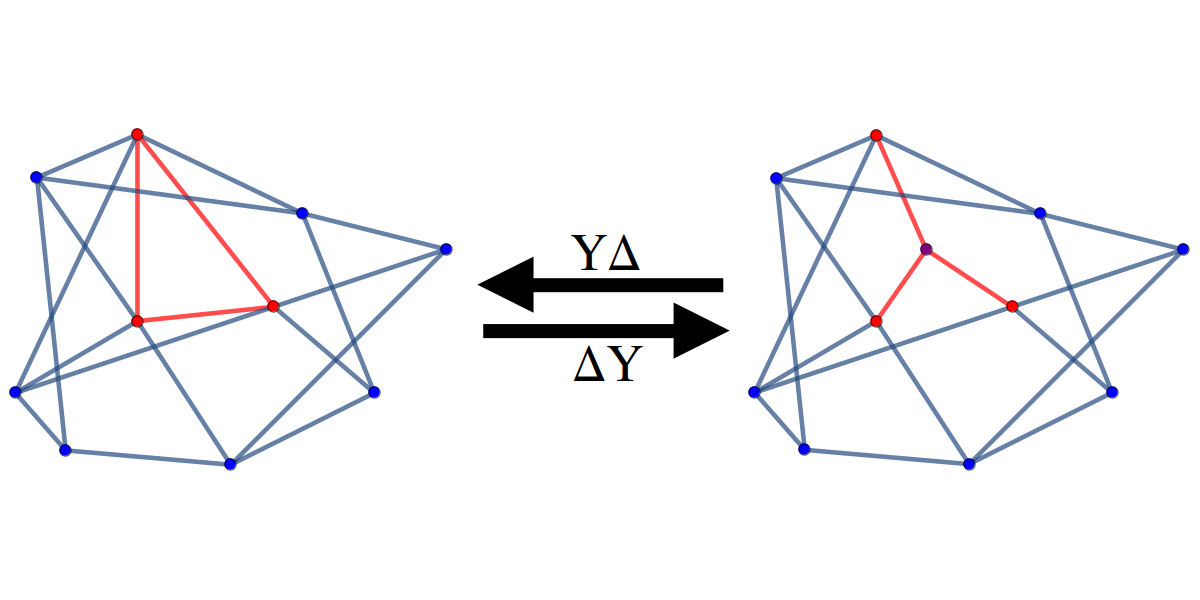
A Mathematica package that contains functions for performing triangle-wye (also delta-wye or ΔY) and wye-triangle (also wye-delta or YΔ) transforms on simple undirected graphs.

The main feature of this package is the function WyeTriangleWyeFamily that can efficiently generate all (or a selection of) graphs that are the result of any sequence of triangle-wye or wye-triangle transforms on a graph.

For further reading, see:

• Y-Δ Transform Wikipedia Article
• Delta-wye-delta transformations: algorithms and applications, Isidoro Gitler
• More Forbidden Minors for Wye-Delta-Wye Reducibility, Yaming Yu (pdf)
• On the delta-wye reduction for planar graphs, K. Truemper
• Four-terminal reducibility and projective-planar wye-delta-wye-reducible graphs, Archdeacon, etal (pdf)

Functions

• TriangleWye[g, {a,b,c}] performs a triangle-wye transform on the triangle given by vertices {a, b, c} in graph g by deleting any edges among the vertices {a, b, c} and adding a new vertex incident to each of {a, b, c}.

• TriangleWyeChildren[g] returns every graph (distinct up to isomorphism) that can be created by performing a triangle-wye transform on some triangle in g. Relies on function TriangleWye.

• TriangleWyeDescendants[g] returns a nested list of all (not necessarily distinct) graphs that can be created by performing a sequence of triangle-wye transforms on g. The nested lists keep track of the family heritage and looks like {graph, TriangleWyeDescendants /@ TriangleWyeChildren[graph]}. Relies on function TriangleWyeChildren.

  To get a flat list of the distinct triangle-wye descendants of g, use

   DeleteDuplicates[Flatten[TriangleWyeDescendants[g]], IsomorphicGraphQ[#1, #2] &]
  

• WyeTriangle[g, v] performs a wye-triangle transform on vertex v in graph g by deleting v and forming a 3-cycle among the neighbors of v. This function fails if VertexDegree[g, v] != 3.

• WyeTriangleParents[g] returns every graph (distinct up to isomorphism) that can be created by performing a wye-triangle transform on some degree 3 vertex in g. Relies on function WyeTriangle.

  WyeTriangleParents[g, True] does the same thing using a stricter definition of a wye-triangle transform where the neighbors of the vertex to be deleted must not be neighbors of each other.

• WyeTriangleAncestors[g] returns a nested list of all (not necessarily distinct) graphs that can be created by performing a sequence of wye-triangle transforms on g. The nested lists keep track of the family heritage and looks like {graph, WyeTriangleAncestors /@ WyeTriangleParents[graph]}. Relies on function WyeTriangleParents.

  WyeTriangleAncestors[g, True] does the same thing using a stricter definition of a wye-triangle transform where the neighbors of the vertex to be deleted must not be neighbors of each other.

  To get a flat list of the distinct wye-triangle ancestors of g, use

   DeleteDuplicates[Flatten[WyeTriangleAncestors[g]], IsomorphicGraphQ[#1, #2] &]
  

• WyeTriangleWyeFamily[g] returns a flattened list of all distinct graphs that can be created by performing a sequence of triangle-wye and wye-triangle transforms on g, where g is either a single graph or a list graphs. Relies on functions WyeTriangleParents and TriangleWyeChildren.

  WyeTriangleWyeFamily[g, Limit, ProgressFlag, LogFlag, Strict, Condition] returns a flattened list of all distinct graphs that can be created by performing a sequence of triangle-wye and wye-triangle transforms on g with a few optional conditions:

  • Limit is a positive integer such that the function will produce only the graphs that are no more than Limit triangle-wye and wye-triangle transforms from g.

  • Set ProgressFlag to True to print some output to indicate the progress of the algorithm. In this output, G is the starting graph (or set of graphs), and each row contains the list of (the sizes of) sets of graphs produced with the same edge count.

  • Set LogFlag to True to produce a simple log file containing the edgelists of the graphs produced.

  • Set Strict to True to use a stricter definition of a wye-triangle transform where the neighbors of the vertex to be deleted must not be neighbors of each other.

  • Condition should be a function that takes a single graph object and returns True or False. If Condition is defined, all graphs (except those of g) that don't satisfy Condition will be immediately discarded from consideration. By default, Condition is GraphQ.

ToDo

• Change the strictness second argument in WyeTriangleParents and WyeTriangleAncestors and all the arguments in WyeTriangleWyeFamily to utilize OptionsPattern[] and OptionsValue[].
• Add a feature to WyeTriangleWyeFamily (and maybe to the Ancestor/Descendent functions too) to produce a graphic of the family showing the lineage.