Revisiting BM Boghosian, PV Coveney, and H Wang. A new pathology in the Simulation of Chaotic Dynamical Systems on Digital Computers, Adv. Theory Simul. 2019, 2, 1900125, DOI: 10.1002/adts.201900125
now published in
Klöwer, M, PV Coveney, EA Paxton and TN Palmer, 2023. Periodic orbits in chaotic systems simulated at low precision, Scientific reports, DOI: 10.1038/s41598-023-37004-4
The corresponding notebook with details on the numerical implementation can be found here.
The generalised Bernoulli map was recently used to analyse a "new pathology" of binary number formats in dynamical systems by Boghosian, Coveney and Wang, 2019. We revisit their results when simulating the generalised Bernoulli map with the following number formats: 16, 32 and 64-bit floating-points numbers, with deterministic and stochastic rounding, 32-bit posits and 16-bit logarithmic fixed-point numbers (logfixs). The numerical collapse of the attractor is confirmed for the special case β=2, which can only be prevented with logfixs whose rounding errors on subtraction preserve the chaotic property better. For the generalised Bernoulli map with varying β the attractor is not found to collapse and better represented with higher precision number formats. Short periodic orbits are found, which, however, extend in period length with more precision, similar as in many other dynamical systems. Despite the periodic orbits, a negligible discrepancy to the analytical invariant measures is found as long as enough precision is provided, especially with Float64 or Float32 with stochastic rounding.
The generalised Bernoulli map is a one-variable chaotic system
xⱼ₊₁ = fᵦ(xⱼ) = βxⱼ mod 1
with a dense attractor for many choices of β>1. Its invariant measures are (Hofbauer, 1978)
hᵦ(x) = C∑ᴺⱼ₌₀ β ⁻ʲ θ(1ⱼ - x)
with xⱼ = fʲᵦ(xⱼ) and 1ⱼ = fʲᵦ(1). The Heaviside function is θ(x) and C a normalisation constant.
This series is evaluated with N→∞, but in practice N=100 sufficies to calculate the invariant measure
at much higher precision than can be obtained from the numerical solution of the Bernoulli map.
For β=2 the Bernoulli map is poorly represented with most binary arithmetics, such as floating-point number or
posits.
The multiplication with β acts as a left-bitshift in binary formats with linearly-spaced significand.
The mod 1 operation maps x ∈ [1,2) to [0,1), which is for floats and posits an error-free subtraction with 1 as
for every x ∈ [1,2) the corresponding x-1 is perfectly representable in the same number number format.
Consequently, an initial condition x₀ at finite precision (i.e. 0s exist implicitly for the unrepresented significant bits)
will yield xₙ = 0 after n time steps as βx sets one signficant bit per iteration to zero, starting from the least significant.
Analytically, any rational initial condition x₀ will show the same behaviour, but irrational x₀ will remain chaotic in time.
As floats or posits only represent rational numbers, their attractors will eventually collapse to x=0 too.
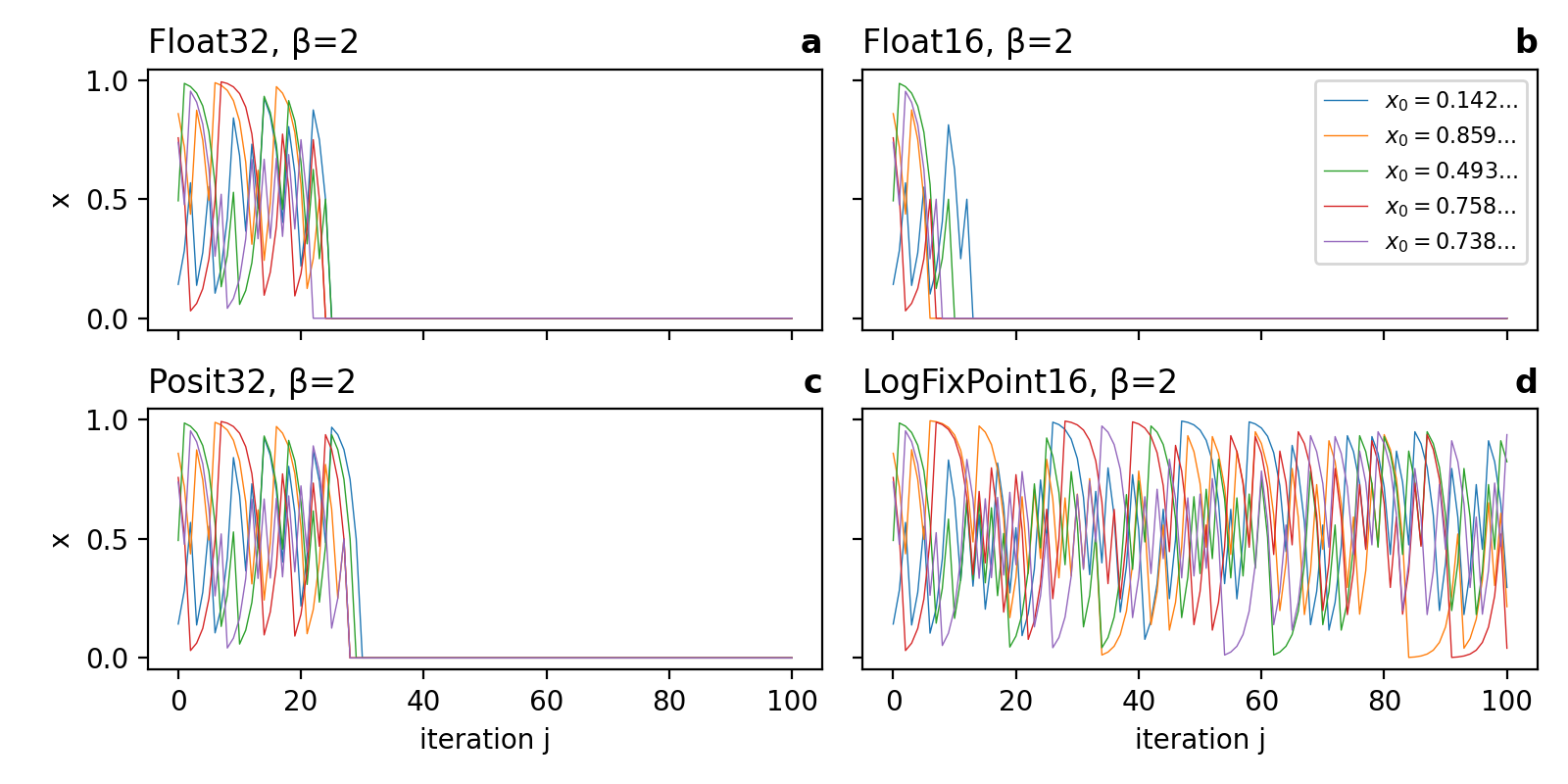
This effect is shown in Fig. 1 for floats (32-bit single-precision Float32 and 16-bit half-precision Float16) and posits (32-bit Posit32). Stochastic rounding as an alternative to the deterministic round to nearest (as in the IEEE-754 standard) has no impact here for Float32 or Float16, as all operations in the Bernoulli map are rounding error-free.
Fig. 1 The Bernoulli map fᵦ for β=2 with different number formats. (a) Float32, (b) Float16, (c) Posit32
and (d) LogFixPoint16 starting from random initial conditions in [0,1). The Bernoulli map f₂ does not introduce arithmetic
rounding errors in (a-c), such that stochastic rounding has no impact. The logfix subtraction in f₂ introduces rounding errors
in (d) that prevent the collapse of the attractor to 0 in (a-c).
Interestingly, the logarithmic-fixed point number format LogFixPoint16 does not
show the collapse of the attractor after (at most) n time steps, which corresponds to the number of significant/fraction bits in
the respective number format. Logfixs are rounding error-free in multiplication, but not in addition, such that the mod 1 operation
of the Bernoulli map yields both 0 or 1 in the least signficant bit, preventing the attractor from collapse. Consequently, the
rounding error for logfixs preserves the chaotic property of the analytical Bernoulli map.
The Hofbauer invariant measure hᵦ(x) of the Bernoulli map are compared with numerical estimations when simulating the system with various number
formats. The Bernoulli map is calculated with an ensemble of Nens = 1000 members (each starting from a different random initial condition)
for Nsteps = 10,000 time steps, discarding a spin-up of 100 time steps. The sample size for x is therefore about 10,000,000, smaller ensembles
or fewer time steps were not found to yield robust statistics. The invariant measures are estimated as histograms h*(x) over x with a
bin-width of 0.025 and normalised to probability 1, ∫₀¹ h*(x) dx = 1.
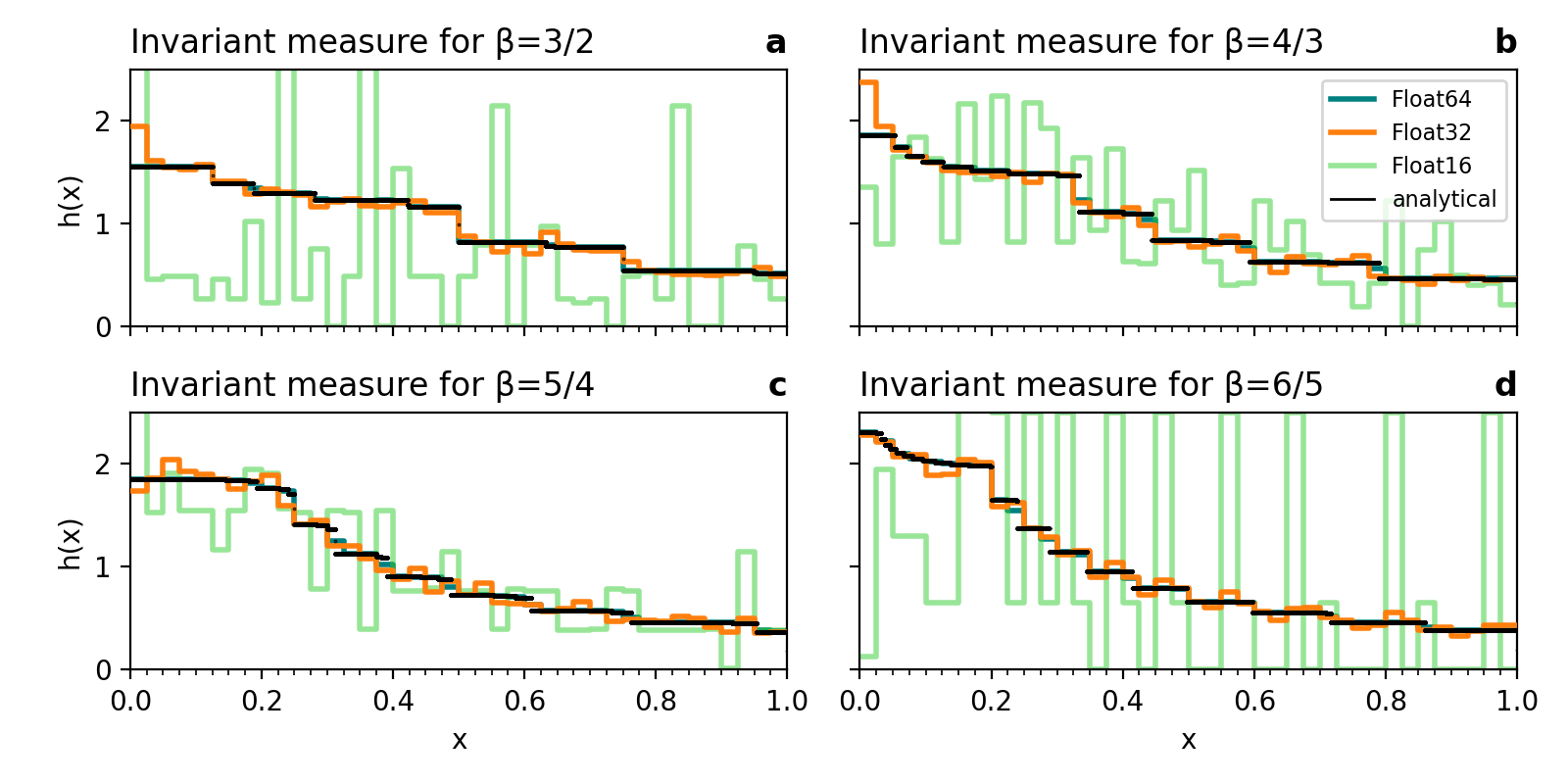
The free parameter β is changed to be 3/2, 4/3, 5/4 or 6/5, such that the multiplication with β in the Bernoulli map is not rounding error-free. The estimated invariant measures resemble the analytical one from Hofbauer, but differ due to rounding errors. Note that the discrete analytical invariant measures do not coincide with the chosen bins, such that the discrete steps are not correctly represented - an artifact from the methodology.
Fig. 2 The invariant measures of the generalised Bernoulli map for β = (a) 3/2, (b) 4/3, (c) 5/4 and (d) 6/5
calculated with different number formats and rounding modes: 64 and 32-bit floating-point numbers (Float64,Float32),
32-bit posits and Float32 with stochastic rounding. The invariant measures are obtained from long integrations of the
Bernoulli map from many different initial conditions x₀ in [0,1). Histograms of x with bin width 0.025 and the
analytical invariant measures are normalised.
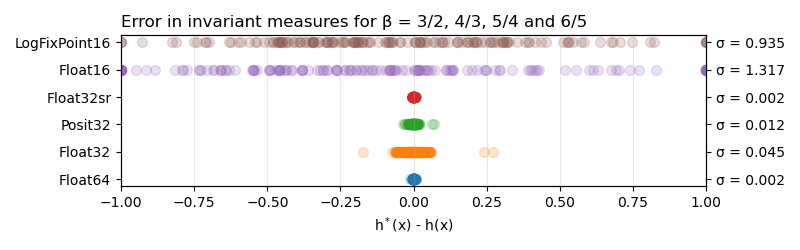
Other than for β=2, where the attractor entirely collapses, the misrepresentation of the invariant measure here is only slight. The question arises whether this is improved with higher precision or with other number formats. The error between the analytical invariant measure and the numerical estimation is shown in Fig. 3. The lower errors with Float64 compared to Float32 confirm that a higher precision reduces the errors in the simulation of the Bernoulli map. All 32-bit formats have a considerably lower error than the 16-bit formats, Float16 and LogFixPoint16, mathing the idea that more precision reduces the overall error in the simulation of dynamical systems. Among the 32-bit formats, Posit32 performs better than Float32, which can be explained with its higher precision of numbers around 1. Stochastic rounding for Float32 drastically reduces the error such that the remaining error is indistinguishable from Float64.
Fig. 3 Error in the invariant measures for the Bernoulli map. The invariant measures h*(x) simulated with different number
formats are quantified from the histograms in Fig. 2. The errors are calculated with respect to the analytical invariant measures
h(x). The standard deviations of the error distributions are denoted with 𝜎. For Float16 and LogFixPoint16 parts of the error
distribution is outside of the axis limits.
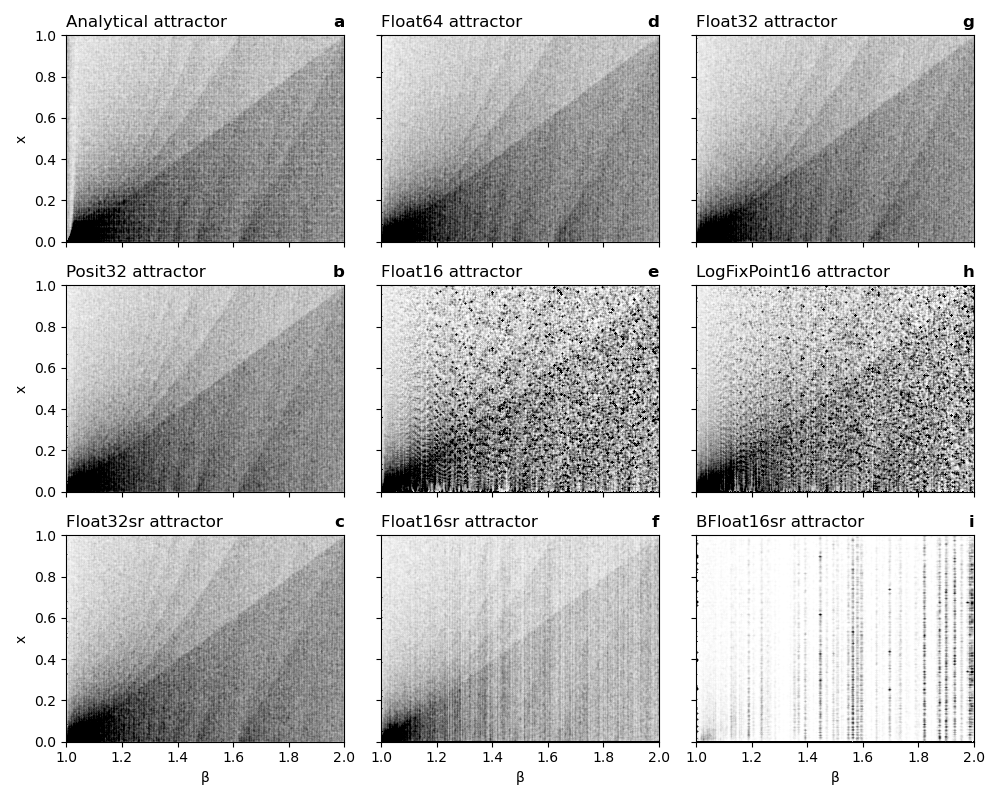
The attractor of the Bernoulli map is dense and although collapsing for β=2 (Fig. 1) similarly dense when simulated with various
number formats for the general case of 1<β<2 (Fig. 5). The invariant measure is slightly changed with Float16 and islands of high probability mass
appear which are an artefact of the 16-bit arithmetic. Some smaller discrepancies can be seen for β not much larger than 1, where
the analytical structure is not well reproduced. Apart from these differences the general invariant measure structure is well simulated
with finite precision arithmetics.
Fig. 4 Analytical attractor and as simulated with various number formats. (a) Analytical attractor sampled from Hofbauer's h(x),
(b-f) attractors obtained from simulation of the generalised Bernoulli map with various number formats: (b) Float64, (c) Float32, (d)
Posit32, (e) Float32 + stochastic rounding, (f) Float16.
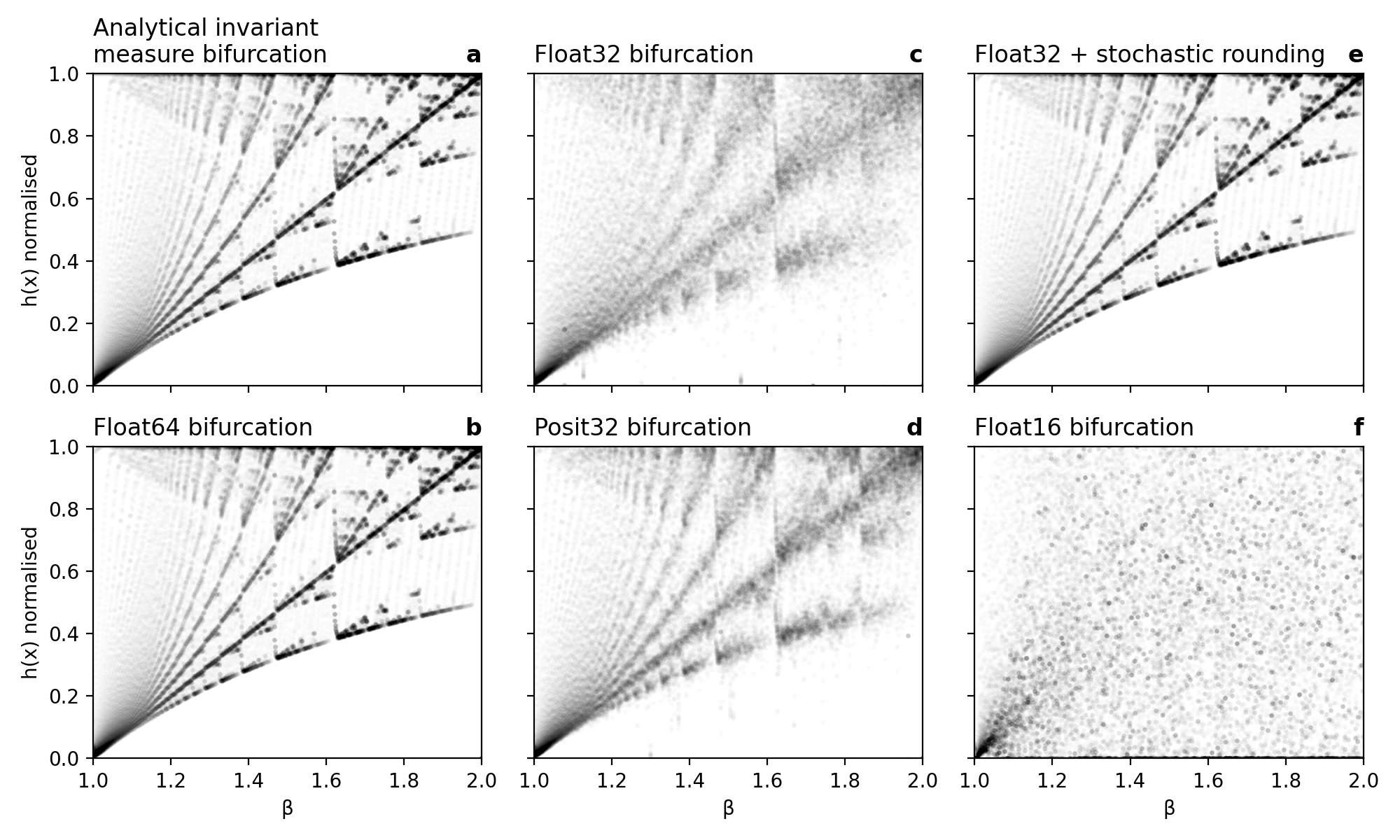
To investigate the structure of the generalised Bernoulli map, we analyse a bifurcation diagram of
the quantization levels of the invariant measures varying β in (1,2).
Although the attractor of the generalised Bernoulli map is dense in [0,1], its invariant measure consists of
discrete quantization levels as shown in Fig. 2. The bifurcation of these levels is visualised in Fig. 4a
as follows from a sampling of the analytical
invariant measure (to keep the methodology consistent and to account
for artifacts as discussed above from the histogram binning),
and from numerical simulations of the generalised Bernoulli map with various number formats.
The analytical bifurcation diagram shows a complex structure that is, in general, very well represented with Float64, Float32 + stochastic rounding, or Posit32 (despite slightly less sharp). Float32 resembles the structure, but appears washed-out as the invariant measures are not as discrete and errors prevail (Fig. 3). The collapse of the attractor, as shown for β=2 in Fig. 1, should therefore be regarded more as a special case due to the vanishing rounding errors. However, the bifurction diagram as results from Float16 arithmetic shows discrepancies, such that 16-bit arithmetic were not found to be sufficient to preserve the invariant measure of the system.
Fig. 5 Bifurcation diagram of the invariant measure h(x) analytically and as simulated with various number formats, varying β.
(a) Analytical invariant measure's bifurcation from Hofbauer's h(x), (b-f) Bifurcation obtained from the histograms of x simulated
with various number formats: (b) Float64, (c) Float32, (d) Posit32, (e) Float32 + stochastic rounding, (f) Float16.
Normalisation is applied with max(hᵦ(x)).