Copyright(c) 2015 Milo Yip (miloyip@gmail.com)
This benchmark evaluates the performance of generting random numbers with standard normal distribution. The function prototypes are:
void normaldistf(float* data, size_t n);
void normaldist(double* data, size_t n);These functions generate n standard normal distributed random numbers (samples), in float and double respectively.
Generating muliple random numbers, instead of generating a single random number, can be suitable for some algorithms (such as Box-Muller generates two numbers at once, and also SIMD versions).
Some implemenetations require data to be 16 or 32 byte aligned, and n to be multiples of 2, 8, 16, 32 etc.
Firstly the program verifies the correctness of implementations. The correctness is simply using the following critera:
bool correctness =
std::abs(mean ) < 0.01 &&
std::abs(sd - 1.0) < 0.01 &&
std::abs(skewness) < 0.01 &&
std::abs(kurtosis) < 0.01;where skewness is Pearson's moment coefficient of skewness and kurtosis is excess kurtosis.
In the benchmark, each trial generates n = 1000000 (1 million) samples. The minimum time duration is measured for 10 trials.
- Obtain premake4.
- Copy premake4 executable to
normaldist-benchmark/buildfolder (or system path). - Run
premake.batorpremake.shinnormaldist-benchmark/build - On Windows, build the solution at
normaldist-benchmark/build/vs2008/or/vs2010/. - On other platforms, run GNU
make config=release32(orrelease64) atnormaldist-benchmark/build/gmake/ - On success, run the
normaldistXXXexecutable is generated atnormaldist-benchmark/ - The results in CSV format will be written to
normaldist-benchmark/result. - Run GNU
makeinnormaldist-benchmark/resultto generate results in HTML.
Note that, for platforms not supporting SSE2/AVX, please modify build/premake4.lua and src/test.h.
| Function | Description |
|---|---|
| boxmuller | Box-Muller transform [1]. Requires n % 2 == 0. |
| cpp11random | std::normal_distribution with std::minstd_rand. |
cltm |
By central limit theorem (CLT), sum m uniform random numbers, then adjust the mean and re-scale for standard deviation. |
| inverse | Inverse transform sampling with inverse normal CDF developed by Peter John Acklam. |
| marsagliapolar | Marsaglia polar method [2]. Requires n % 2 == 0. |
| ziggurat | Ziggurat algorithm by Marsaglia et al [3], using Jochen Voss's implementation. |
| null | Generates uniform random numbers. |
Note that the null implementation generates unform random numbers. It measures the overheads of looping, memory writing, and uniform random number generation. Uniform number generation is included because normally distributed random number generators are based on at least one uniform random number generation.
CLT implementations were actually unable to pass the correctness tests, as their kurtosis are higher than threshold.
All implementations except cpp11random uses simplest linear congruential generator as uniform distributed pseudo random number generator (PRNG).
| Suffixes | Description |
|---|---|
| sse2 | SSE2 version (data requires 16-byte alignment) |
| avx | AVX version (data requires 32-byte alignment) |
Some implementations of sse2 and avx version are using math libraries sse_mathfun and avx_mathfun, which provides logarithm and sine/cosine functions.
The following are results measured on a iMac (Core i5 3330S @2.70GHz).
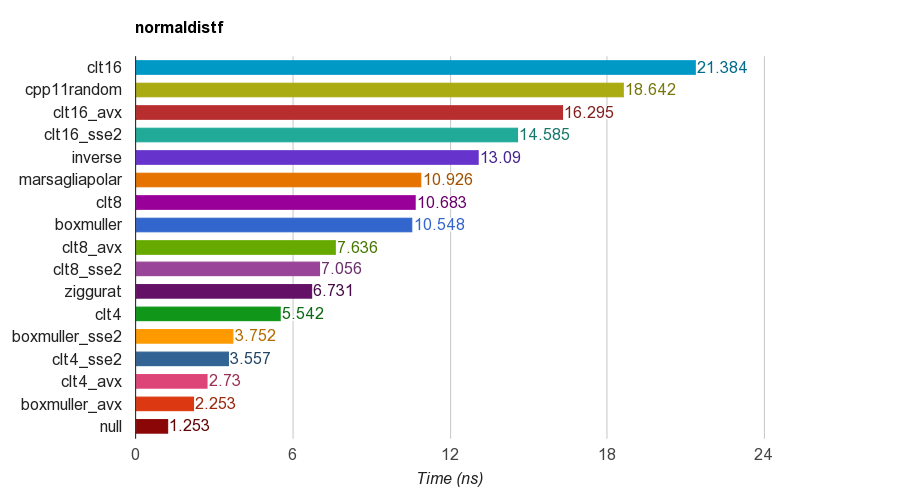
normaldistf (single precision):
| Function | Time (ns) | Speedup |
|---|---|---|
| clt16 | 21.384 | 1.00x |
| cpp11random | 18.642 | 1.15x |
| clt16_avx | 16.295 | 1.31x |
| clt16_sse2 | 14.585 | 1.47x |
| inverse | 13.090 | 1.63x |
| marsagliapolar | 10.926 | 1.96x |
| clt8 | 10.683 | 2.00x |
| boxmuller | 10.548 | 2.03x |
| clt8_avx | 7.636 | 2.80x |
| clt8_sse2 | 7.056 | 3.03x |
| ziggurat | 6.731 | 3.18x |
| clt4 | 5.542 | 3.86x |
| boxmuller_sse2 | 3.752 | 5.70x |
| clt4_sse2 | 3.557 | 6.01x |
| clt4_avx | 2.730 | 7.83x |
| boxmuller_avx | 2.253 | 9.49x |
| null | 1.253 | 17.07x |
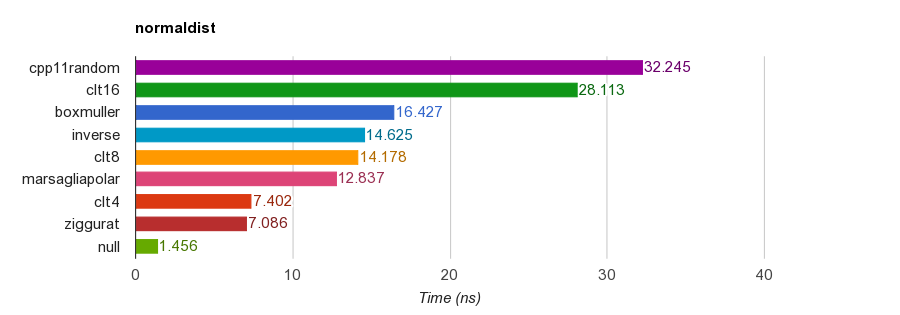
normaldist (double precision):
| Function | Time (ns) | Speedup |
|---|---|---|
| cpp11random | 32.245 | 1.00x |
| clt16 | 28.113 | 1.15x |
| boxmuller | 16.427 | 1.96x |
| inverse | 14.625 | 2.20x |
| clt8 | 14.178 | 2.27x |
| marsagliapolar | 12.837 | 2.51x |
| clt4 | 7.402 | 4.36x |
| ziggurat | 7.086 | 4.55x |
| null | 1.456 | 22.15x |
-
How to add an implementation?
You may clone an existing implementation file (e.g.
boxmuller.cpp). And then modify it. Re-runpremaketo add it to project or makefile. Note that it will automatically register to the benchmark by macroREGISTER_TEST(name).Making pull request of new implementations is welcome.
[1] G. E. P. Box and Mervin E. Muller, A Note on the Generation of Random Normal Deviates, The Annals of Mathematical Statistics (1958), Vol. 29, No. 2 pp. 610–611.
[2] Marsaglia, George, and Thomas A. Bray. "A convenient method for generating normal variables." SIAM review 6.3 (1964): 260-264.
[3] Marsaglia, George, and Wai Wan Tsang. "The ziggurat method for generating random variables." Journal of statistical software 5.8 (2000): 1-7.