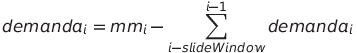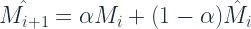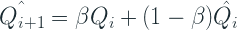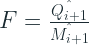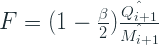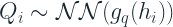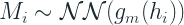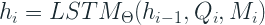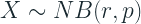Paper deep AR y deep renewal processes for intermitent demand de amazon , implementación a través de gluonts y MX-NET, también se usan redes lstm para hacer baselines del problema.
Esta en desarrollo, este repo, quedan partes por implementar ...
Documentación de los modulos con sphinx
build/html/index.html$ git clone https://github.com/matheus695p/deep-ar.git
$ cd deep-ar
$ pip install -r requirements.txtEj: a través de anaconda, tiene que ser en ambiente con python=3.6
$ conda create -n deepAR python=3.6 anaconda
$ conda activate deepAR
$ conda install pip
$ pip install pytorchts==0.3.1
$ echo en mi caso necesitaba install cudnn para correr en la GPU
$ pip install torch==1.8.1+cu111 torchvision==0.9.1+cu111 torchaudio===0.8.1 -f https://download.pytorch.org/whl/torch_stable.html
$ pip install pandas==1.0.5
$ pip install tensorflow-gpu==2.4.0 (esto en mi caso dado el cudnn que tenía instalado)tree del proyecto
│ .gitignore
│ README.md
│ requirements.txt
├───codes
│ ├───electricity
│ │ main.py ---> códicos para hacer predicción de demanda de electricicdad
│ │
│ └───manufacturing
│ main.py ---> códicos para hacer predicción de demanda de skus, caso de manufactura
│ transformations.py ---> códicos para transformación al formato de datos de gluonts
├───data
│ LD2011_2014.txt
│ manufacturing.csv
│ raw_manufacturing.csv
├───docs
├───documents
│ paper-amazon-deepAR.pdf ---> paper de deep autoregresive neural networks
│ paper-gluontsTS.pdf ---> paper de la implementación en gluonts
├───images ---> resultados para los difererentes casos
│ caso_electricidad_{nombre}.png
│ caso_manufactura_{nombre}.png
├───results ---> resultados para los difererentes casos
│ │ resultados_energia.csv
│ │ resultados_manufactura.csv
│ ├───energy-model ---> modelo de energia
│ │ input_transform.json
│ │ parameters.json
│ │ prediction_net-0000.params
│ │ prediction_net-network.json
│ │ type.txt
│ │ version.json
│ └───manufacturing-model ---> modelo de manufactura
│ input_transform.json
│ parameters.json
│ prediction_net-0000.params
│ prediction_net-network.json
│ type.txt
│ version.json
└───src
│ module.py ---> módulo de funciones
└───__init__.pyLos scripts utilizados para hacer las pruebas se pueden encontrar en
├───codes
│ ├───electricity
│ │ main.py ---> códicos para hacer predicción de demanda de electricicdad
│ └───manufacturing
│ main.py ---> códicos para hacer predicción de demanda de skus, caso de manufactura
│ transformations.py ---> códicos para transformación al formato de datos de gluonts
│ stationary_tests.py ---> códicos para verificar estacionaridad de las series de tiempoLos datos manejados son de supply, los que equivalen a la demanda de diferentes articulos en el tiempo de una empresa manufacturera, para probar deep AR se eligen los sku's con mayor cantidad de ventas realizadas en el tiempo, de tal manera de abarcar el 80/20 de la producción. En el caso de manufactura es más complejo el preprocesamiento de las series de tiempo, dado que a diferencia del caso academico de energia, es necesario: (1) Hacer tests estadísticos de estacionaridad, (2) En el caso de que no sean estacionarias, por resultado del test, es necesario aplicar técnicas, para llevarlas a ser estacionarias, con el fin de que los módelos de forecasting, tengan el trabajo más fácil. (3) Entrenar modelos con arquitecturas deep AR (4) finetuning a los módelos.
Para el preprocesamiento de los datos, solo se trabajara en esta prueba de conceptos con bases de sku's, existen al rededor de 30.000 sku's diferentes, por lo que se hace imposible realizar modelo para cada sku, además las para ellos se extraen las bases de un sku y con ellas se trabaja.
- SKU = METAL # 4.5|11|540|DO|COMPANY|ZP48 ZAMAC
- BASE_SKU = METAL # 4.5
De esta forma se reduce a trabajar solamente con 19 productos, del total de sku's que son las base del 80/20 de la empresa en cuestión. formato usado para el ingreso de los datos a deepAR:
─── columnas: bases de sku
│
│
filas: compras
realizadas de
esa base de
sku¿Cómo manejar los largos períodos sin demanda que no siguen un patrón específico?"
La respuesta esta pregunta es Análisis de demanda intermitente o Análisis de datos dispersos, esto pasa cuando existen "muchos ceros" en relación con el número de no ceros. El problema es que hay dos variables aleatorias, la primerisima es el tiempo entre eventos (a tu elección) y el tamaño esperado del evento. Si vemos gráficos de autocorrelación (acf) del conjunto completo de lecturas no tiene ningún sentido debido a que la secuencia de ceros realza falsamente el acf (no hay ningún patrón). Hay un par de enfoques para resolver esto, en primera instancia nos quedaremos con el más fácil (spoiler: última)
- Podemos seguir el "método de Croston", que es un procedimiento basado en modelos en lugar de un procedimiento basado en datos. El método de Croston es vulnerable a valores atípicos y cambios / tendencias / cambios de nivel en la tasa de demanda, es decir, la demanda dividida por el número de períodos desde la última demanda.
- Un enfoque mucho más riguroso podría ser buscar "Datos dispersos - Datos desigualmente espaciados" o búsquedas como esa.
- Una solución bastante ingeniosa y simple es el smothing. Si una serie tiene puntos de tiempo en los que surgen ventas y largos períodos de tiempo en los que no surgen ventas, es posible convertir las ventas en ventas por período dividiendo las ventas observadas por el número de períodos sin ventas obteniendo así una tasa. Entonces es posible identificar un modelo entre la tasa y el intervalo entre las ventas que culminan en una tasa pronosticada y un intervalo pronosticado. Esto de manera más sencilla se transforma en una media movil.
Hay algunas nociones más detalladas de estacionariedad que puede encontrar si profundiza en este tema. Son: Son:
- Proceso estacionario (stationary process): proceso que genera una serie estacionaria de observaciones.
- Modelo estacionario (stationary model): un modelo que describe una serie estacionaria de observaciones.
- Tendencia estacionaria (trend c): una serie de tiempo que no muestra una tendencia.
- Estacional por periodos (seasonal stationarity): una serie de tiempo que no exhibe estacionalidad.
- Estrictamente estacionario (strictly (stationary model)): una definición matemática de un proceso estacionario, específicamente que la distribución conjunta de observaciones es invariante al cambio de tiempo.
Podemos usar una prueba estadística para verificar si la diferencia entre dos muestras de variables aleatorias gaussianas es real o una casualidad estadística. Podríamos explorar pruebas de significación estadística, como la prueba t de Student. En esta parte del trabajo, se utiliza una prueba estadística diseñada para comentar explícitamente si una serie de tiempo univariante es estacionaria. El test se llama Augmented Dickey-Fuller.
Hay una serie de pruebas de raíz unitaria y Augmented Dickey-Fuller puede ser una de las más utilizadas. Utiliza un modelo autorregresivo y optimiza un criterio de información a través de múltiples valores de retardo (lags) diferentes. La hipótesis nula de la prueba es que la serie de tiempo se puede representar mediante una raíz unitaria, que no es estacionaria (tiene alguna estructura dependiente del tiempo). La hipótesis alternativa (que rechaza la hipótesis nula) es que la serie de tiempo es estacionaria.
- Hipótesis nula (H0): si no se rechaza, sugiere que la serie de tiempo tiene una raíz unitaria, lo que significa que no es estacionaria. Tiene alguna estructura dependiente del tiempo --> problemas.
- Hipótesis alternativa (H1): Se rechaza la hipótesis nula; sugiere que la serie de tiempo no tiene una raíz unitaria, lo que significa que es estacionaria. No tiene una estructura dependiente del tiempo.
Voy a interpretar este resultado utilizando el valor p de la prueba. Un valor p por debajo de un umbral (como 5% o 1%) sugiere que rechazamos la hipótesis nula (estacionaria); de lo contrario, un valor p por encima del umbral sugiere que no rechazamos la hipótesis nula (no estacionaria), este es el lo clásico en tests estadísticos.
- Valor p> 0.05: No se rechaza la hipótesis nula (H0), los datos no son estacionarios
- Valor de p <= 0.05: Rechaza la hipótesis nula (H0), los datos son estacionarios
Los resultados se pueden ver en results/stationary_test_manufacturing, acá un ejemplo de los 3 primeros, las series de tiempo trabajadas son estacionarias
Para la columna: SP40
Rechaza la hipótesis nula (H0), los datos son estacionarios
ADF estadisticas: -6.757590
Valor de p: 0.000000
Valores criticos:
1%: -3.436
5%: -2.864
10%: -2.568
Para la columna: SP60-S
Rechaza la hipótesis nula (H0), los datos son estacionarios
ADF estadisticas: -5.848840
Valor de p: 0.000000
Valores criticos:
1%: -3.436
5%: -2.864
10%: -2.568
Para la columna: MP60-S
Rechaza la hipótesis nula (H0), los datos son estacionarios
ADF estadisticas: -5.881735
Valor de p: 0.000000
Valores criticos:
1%: -3.436
5%: -2.864
10%: -2.568Los resultados de las redes lstm fueron bastante buenos en el dataset de moving_avarege, al mismo nivel que deep AR De las 19 series de tiempo en 16/19 de las series tuvieron un mape (mean porcentage error) menor 30 % y la accuracy promedio fue de 77.16 % de todos los modelos juntos.
Este es un excelente resultado excelente sabiendo la dificultad que existe en la predicción con series de tiempo que son intermitentes
Resultados Los resultados se pueden encontrar en la carpeta:
results/lstm/*.pngAlgunos resultados:
Los resultados anteriores, corresponden a las predicciones sobre un dataset tratado a través de medias móviles, esto no nos dice nada a simple vista, solo que somos capaces de predecir cual será la media movil futura. Es por eso que sobre estos resultados, es necesario hacer una transformación para determinar la demanda en un punto i del tiempo.
Usamos la siguiente técnica de descompresión ver ecuación:
Donde:
- mmi: Es la media movil del periodo (acá se hizó con 30 días)
- demanda i: Es la demanda en el punto i (acá se hizó con 30 días)
- sumatoria de la demanda hasta el día antes: Es la demanda en el punto i (acá se hizó con 30 días)
- En cada punto i, se debe escoger el máximo entre la demandai y 0, de modo de seguir con la distribución propuesta por la predicción de la red
Entonces, al ser capaces de predecir la medía movil del primer día, al conocer la demanda de los últimos 29, podemos saber cual es la demanda en el punto i, del mismo modo ahora para el caso de i + 1, en donde ahora es conocida la demanda i, que viene dada por la predicción de la media movil.
De esta forma, podemos descomprimir los resultados de predicciones de medias moviles futuras, en demandas en puntos especificos del tiempo.
Al hacer esto, tenemos cual sería la predicción de la demanda en el tiempo, dado el modelo general.
Acá dejo un link a la tabla con los resultados de cada uno de estos modelos.
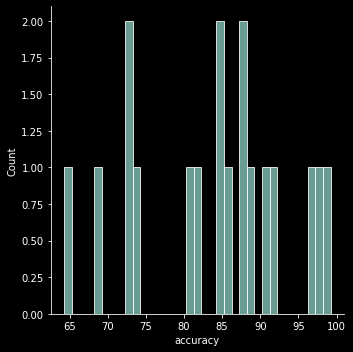
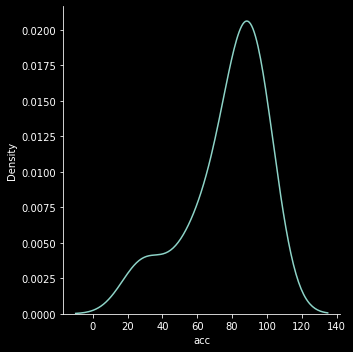
Los resultados son buenismos, acá la distribución de error esperada del conjunto de series de tiempo.
Muy buenas predicciones !!!
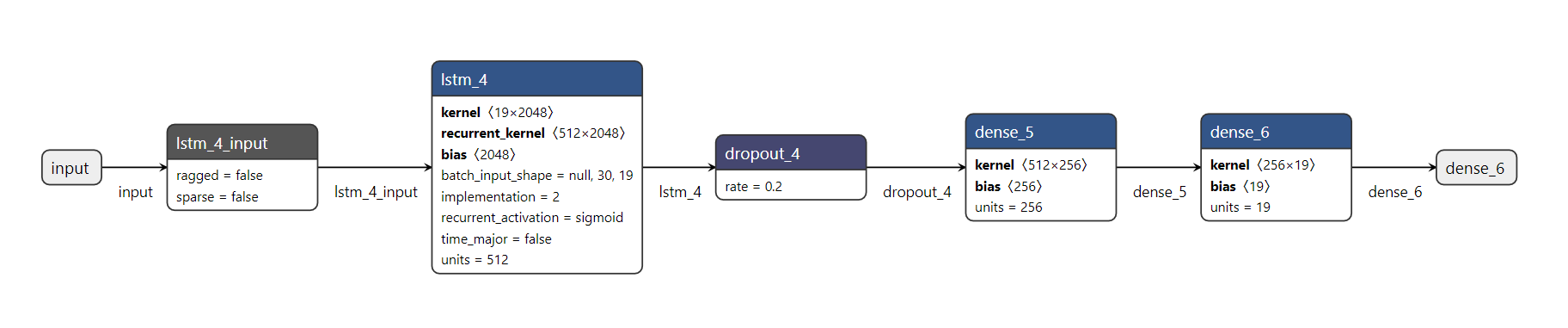
La es una LSTM con 512 neuronas LSTM en la primera capa, mas 256 neuronas Dense en la segunda capa, la capa de salida es del tamaño de la cantidad de Bases de SKU que se hicieron. La regularización de la red se hizo con dropout a tasa de 0.2.
Visualización hecha a través de netron/ re buen visualizador de arquitecturas, recomendado !!!
¿Como avanzamos?
Para un periodo de 45 días, se es capaz de predecir de manera precisa cual sería el total de la demanda en un periodo T de tiempo (cuantos articulos iban a requerir de tal tipo), el problema es que el método de decompresión usado, sesga los subperiodos (díás) en lo que se hace efectiva esta demanda de producción, dado que va escogiendo el máximo entre la demanda del día i y 0, por lo tanto es super improbable acertar a los días exactos en el que se realizó la demanda (intermitencia en los datos). Sin embargo de manera global (en un periodo T) se hace bien, que es lo que le interesa al cliente.
Finalmente conseguimos una accurracy promedio del 83 %, con la mediana en 85 %, lo que es super elevado, sabiendo que un solo modelo maneja 19 bases de SKU. La distribución mostrada anteriormente es reflejo de esto.
Para poder avanzar más en estos resultados, necesitamos ir a buscar esta distribución de la demanda en un periodo T de tiempo, es ahí donde se introduce el paper de amazon deep autoregressive models.
De el modelamiento anterior surge la necesidad de encontrar la distribución de probabilidad de la demanda durante los dias de la predicción, y es en este punto donde entran los modelos probabilisticos como deep AR. Dado que este punto, se ha construido un modelo muy preciso en saber cual sera la demanda en un periodo de tiempo, pero no como va a ocurrir en ese periodo, y es en este punto en donde entra esta solución.
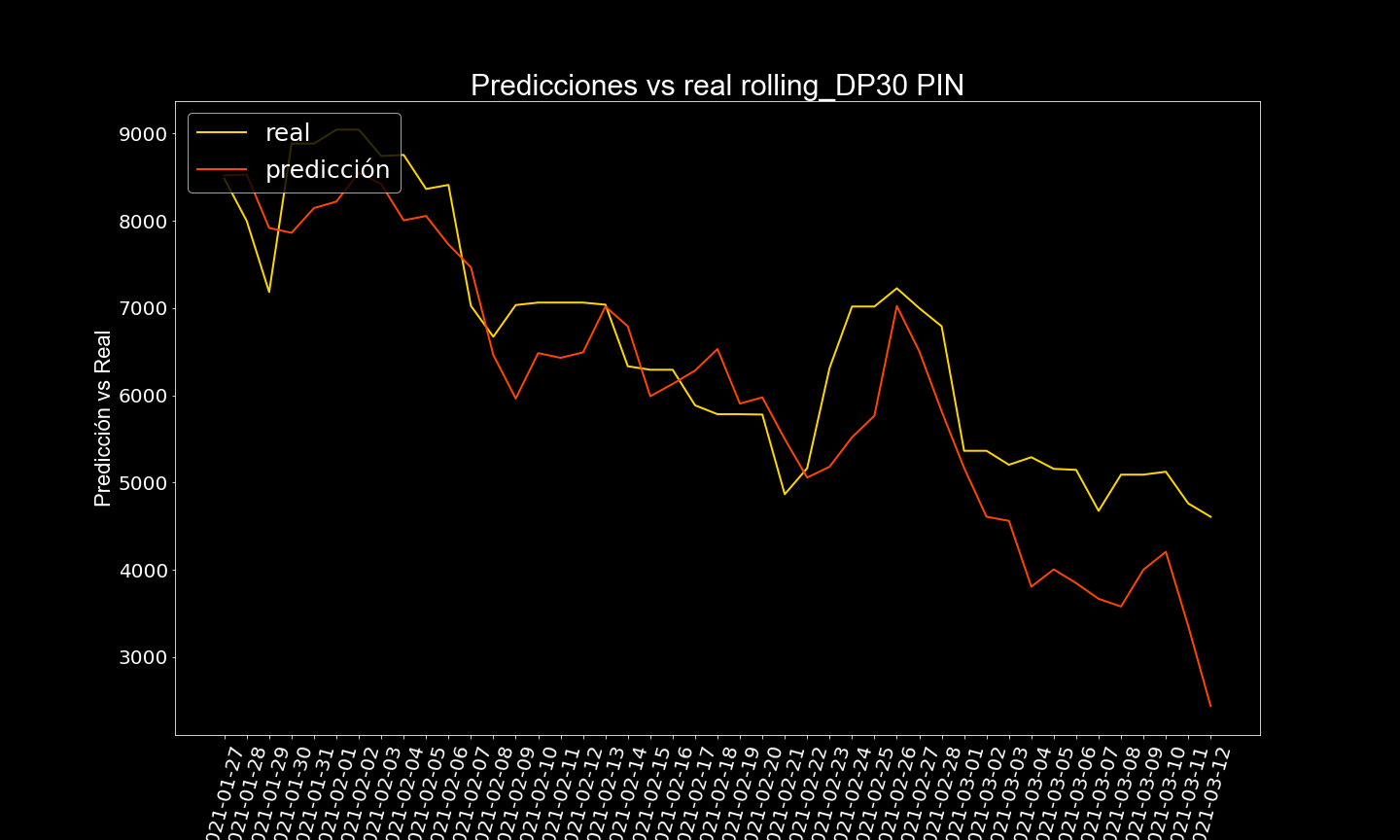
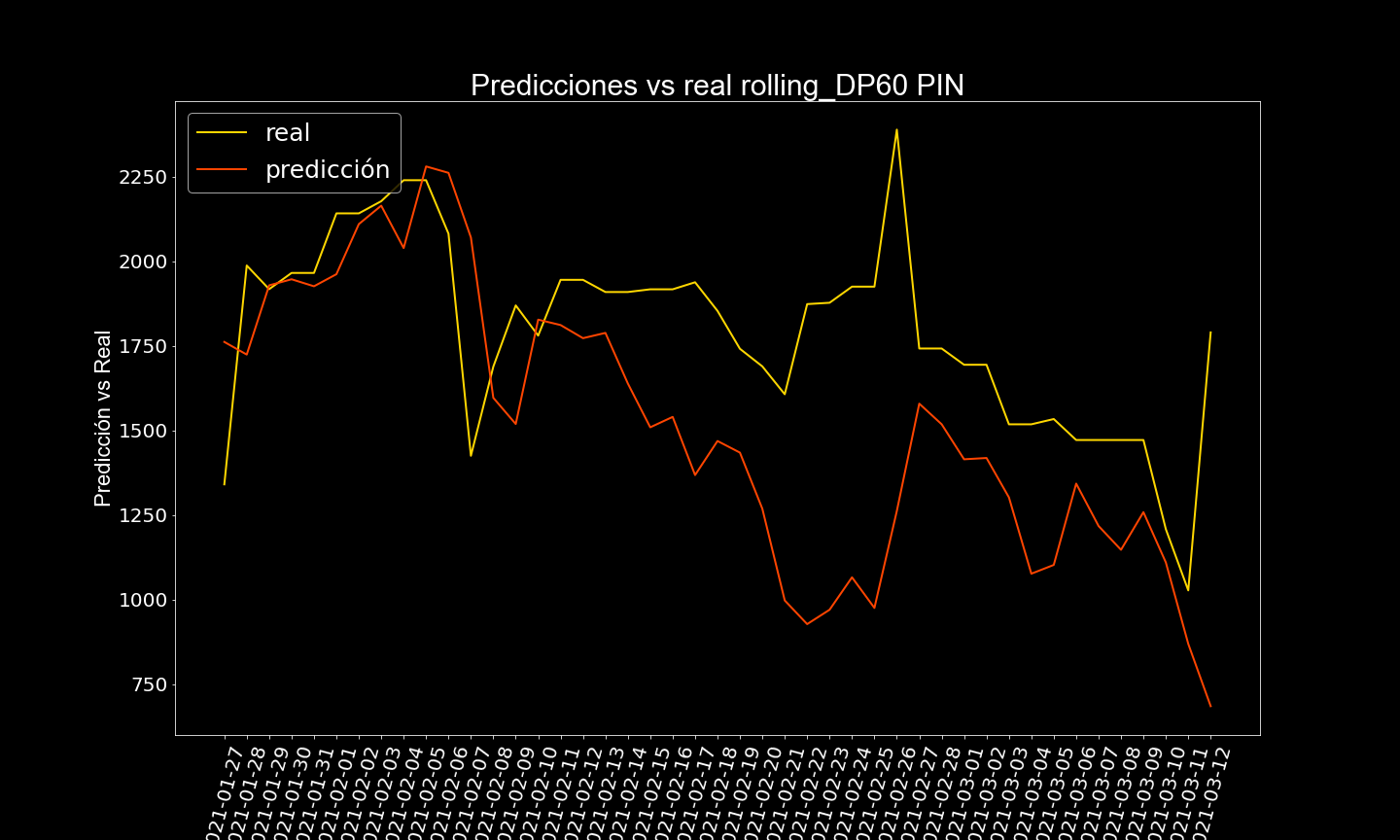
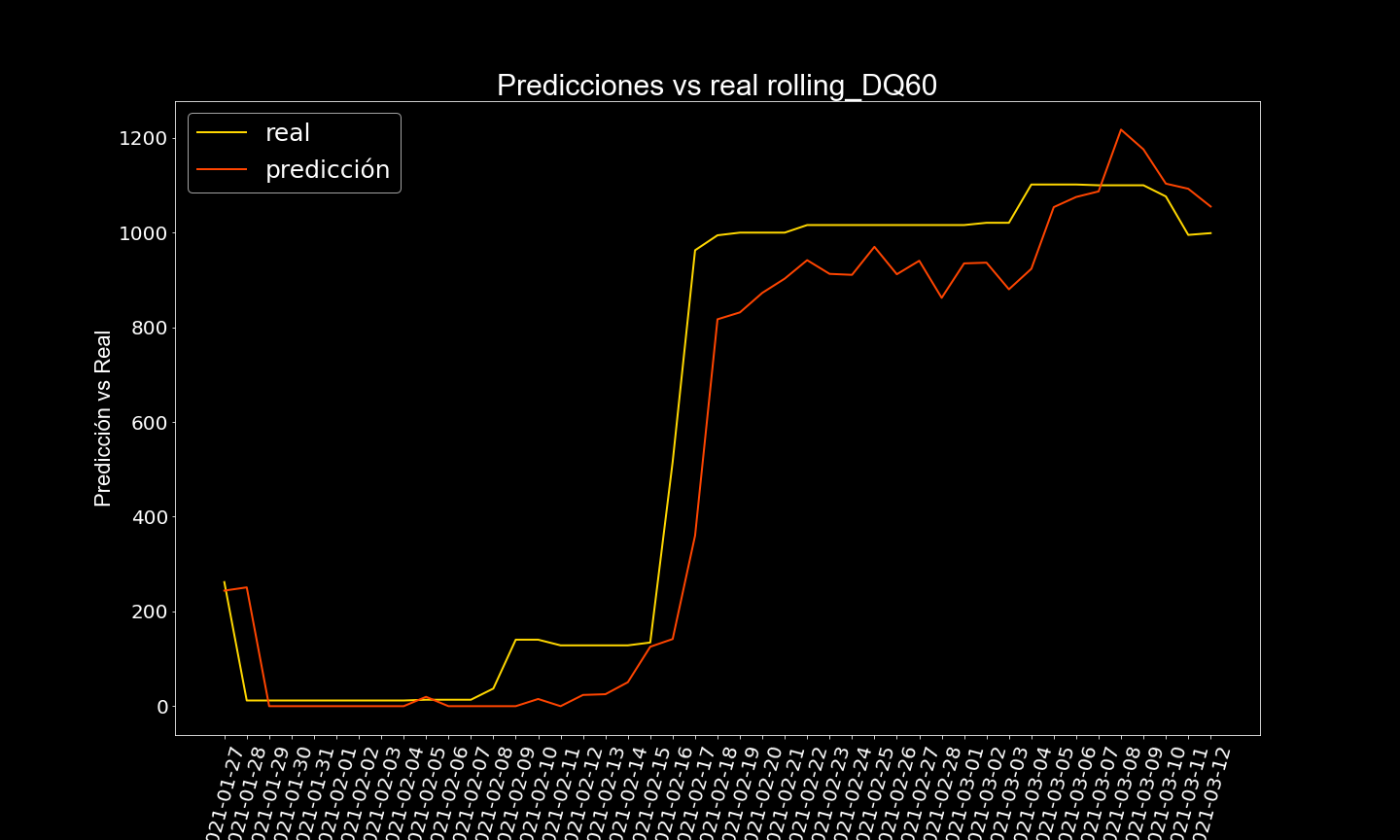
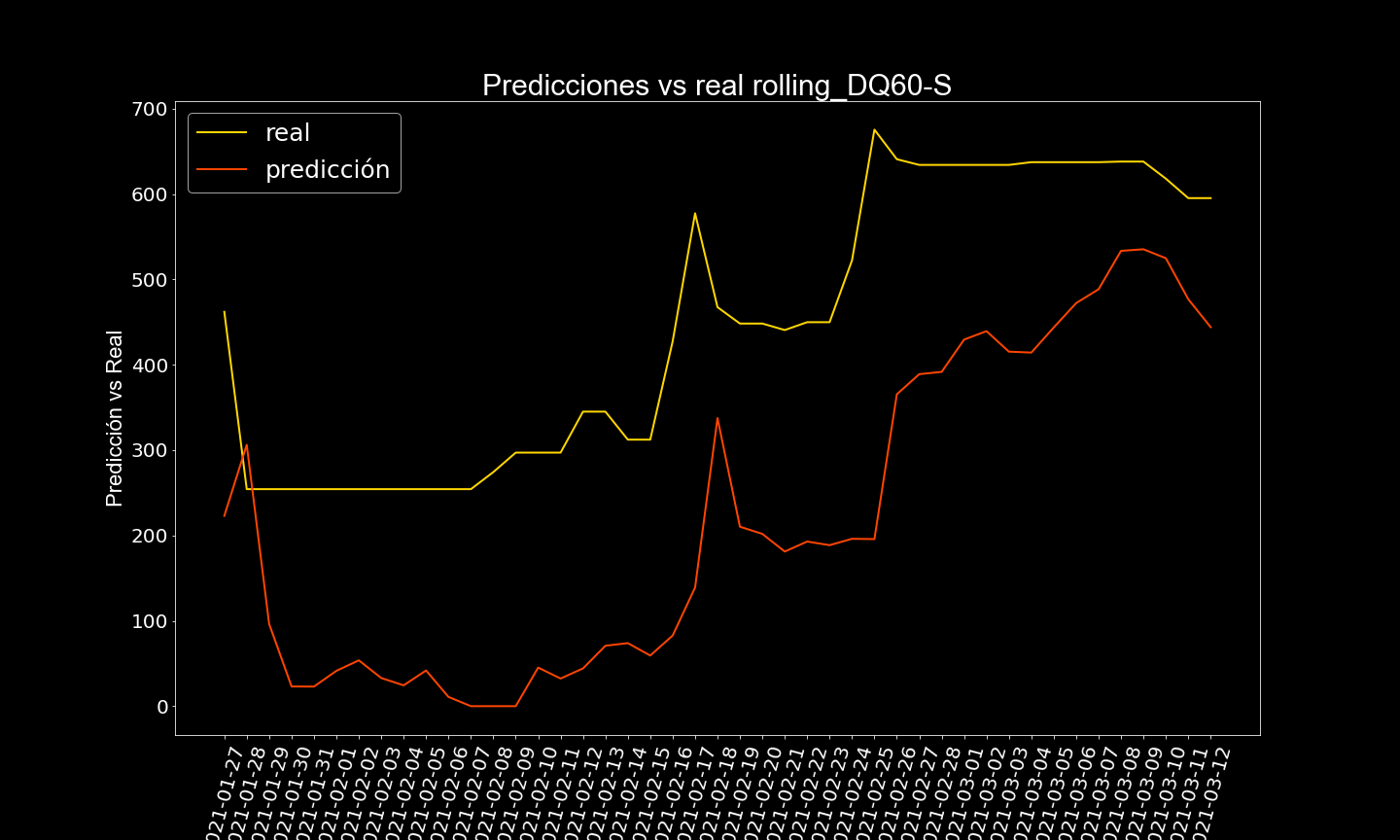
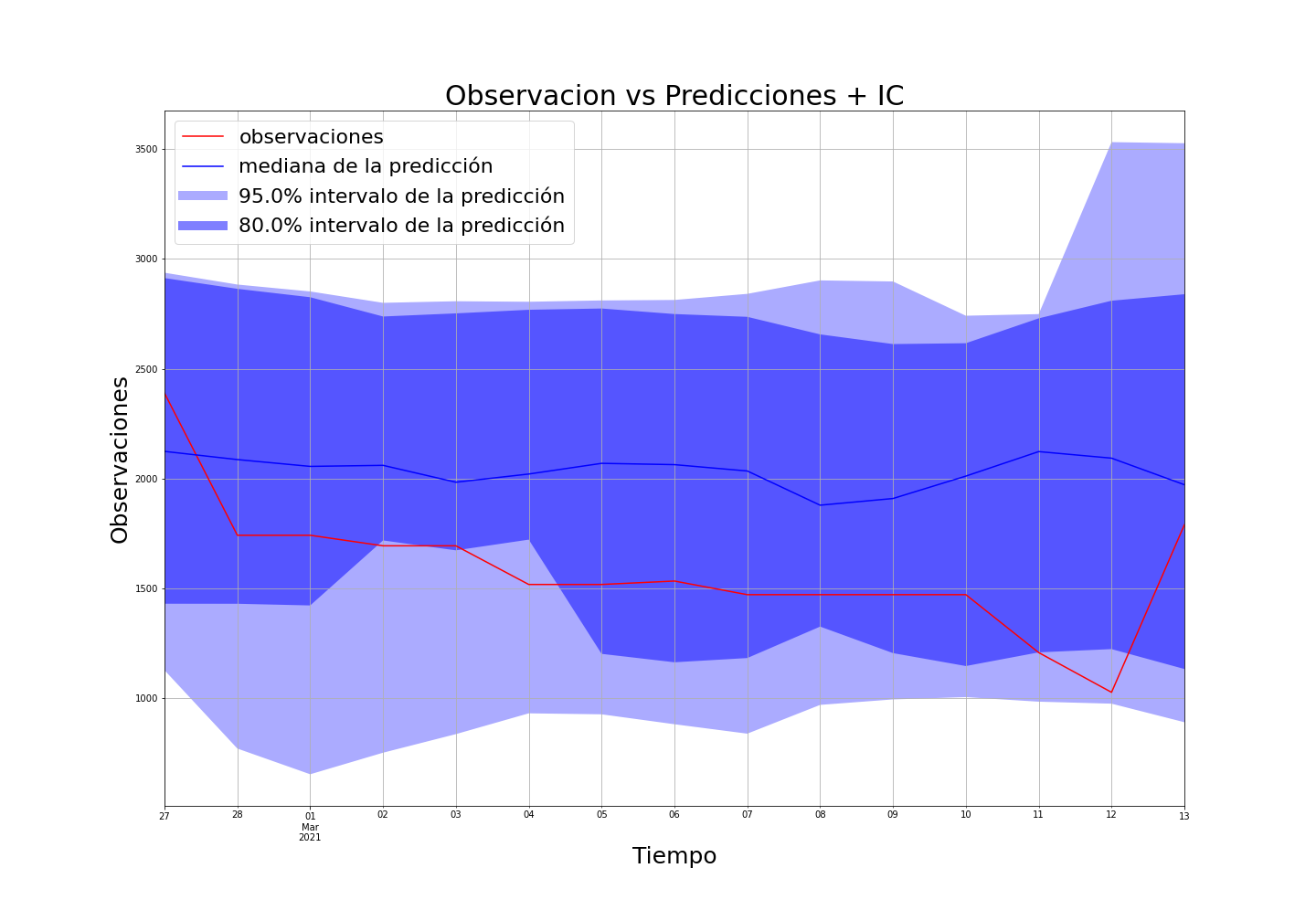
Después de varías pruebas, se determinó que la frecuencia de predicción sería de 14 días, es decir a partir de la última fecha en train, se predice 14 días al futuro, dos semanas, lo ideal es que se hagan predicciones cada 2 semanas, considerando los datos anteriores.
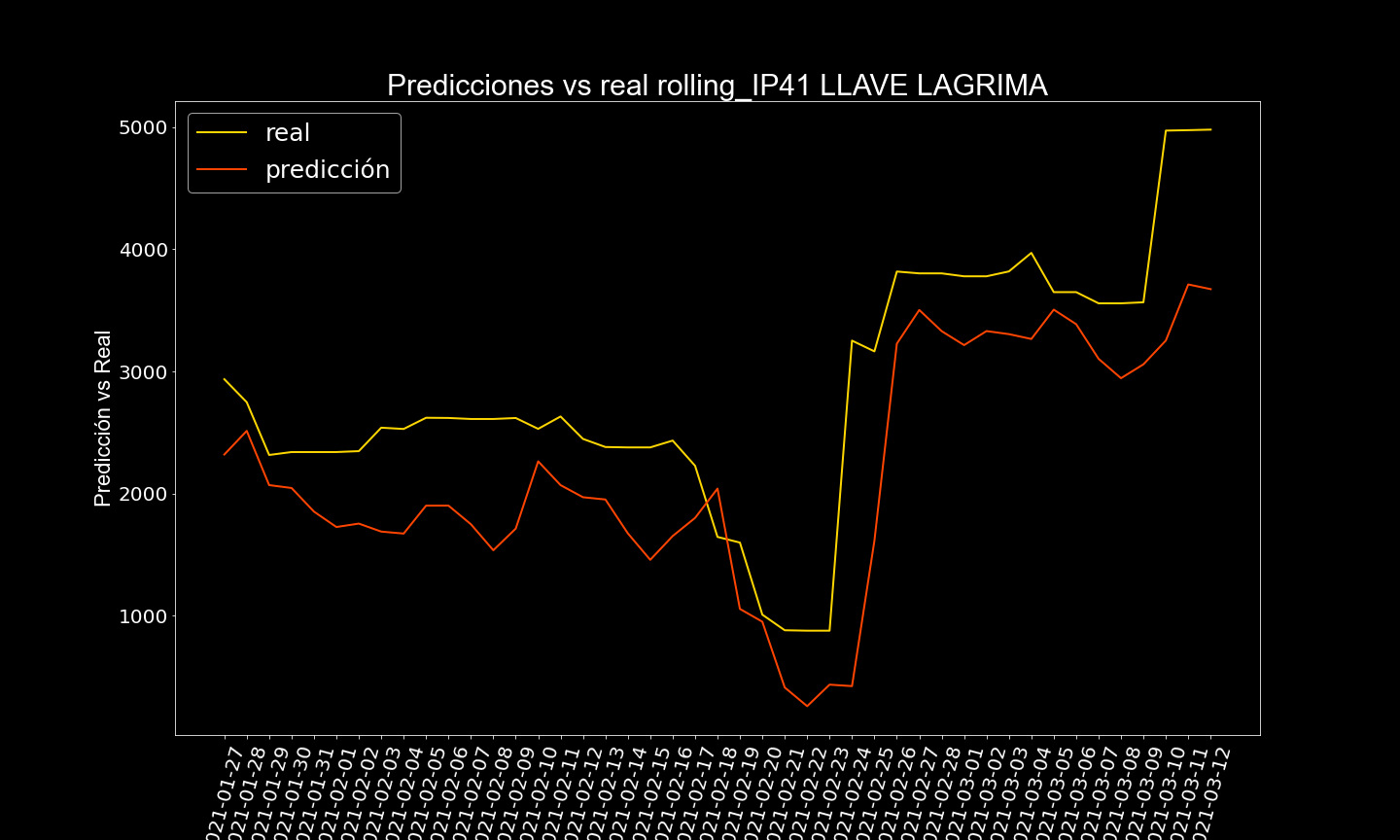
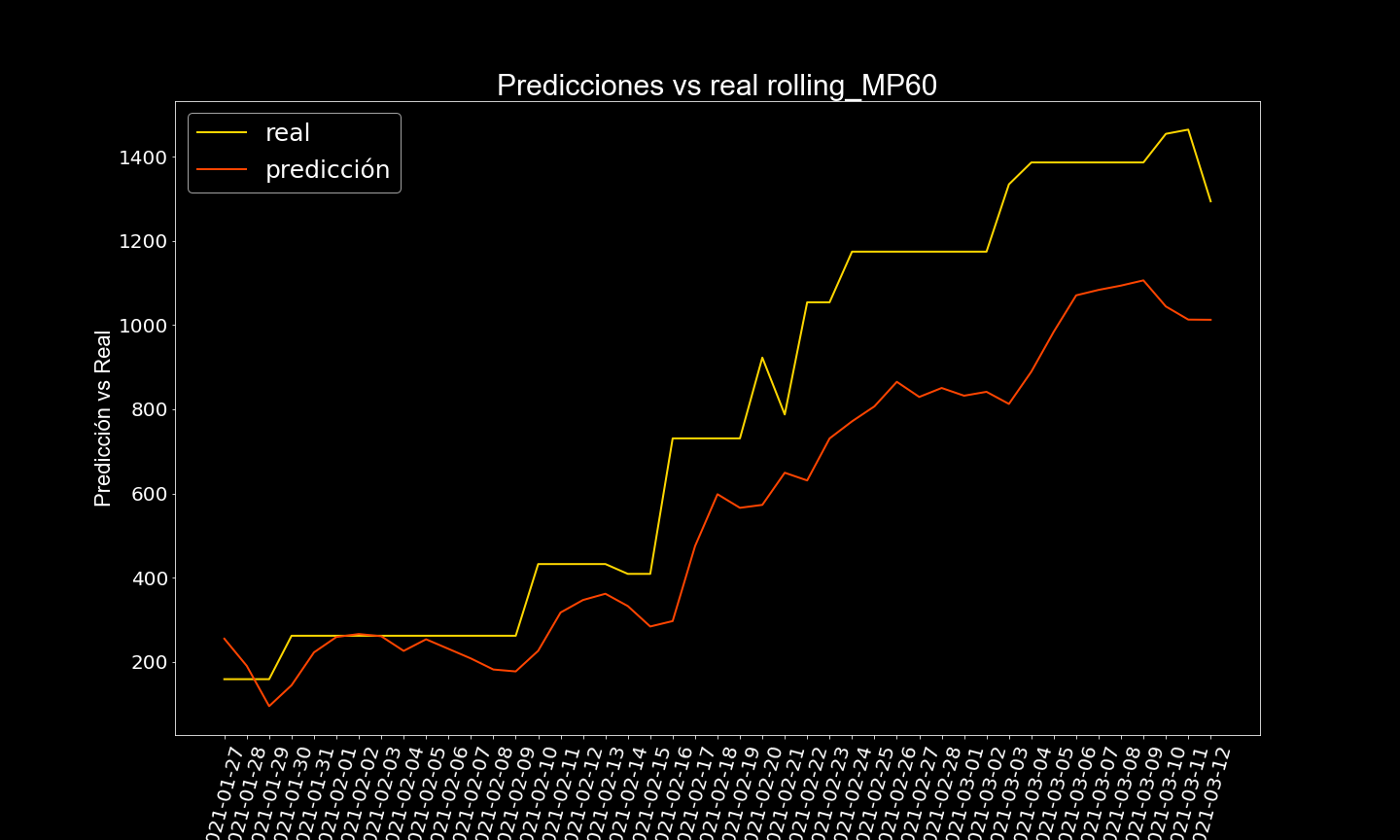
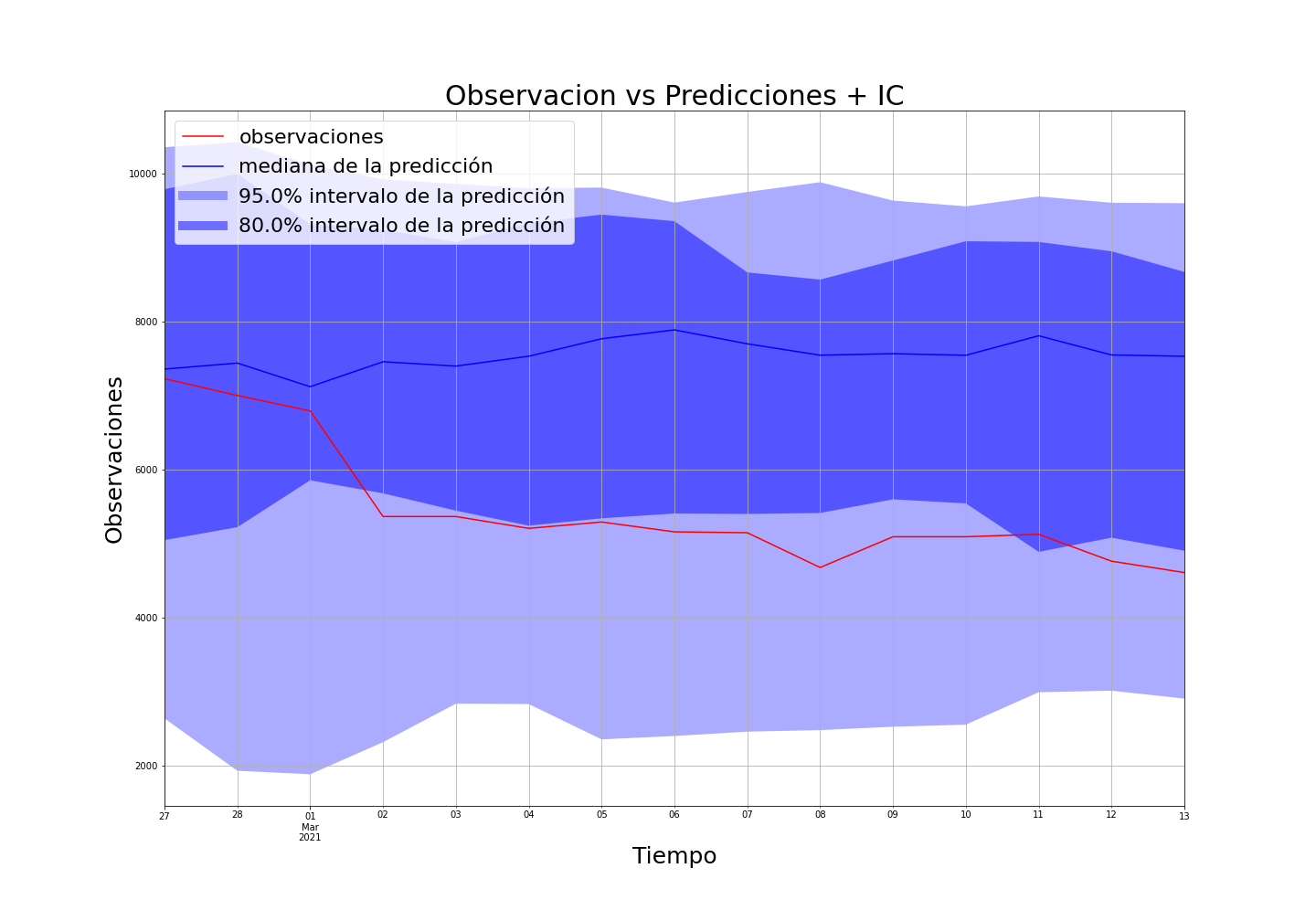
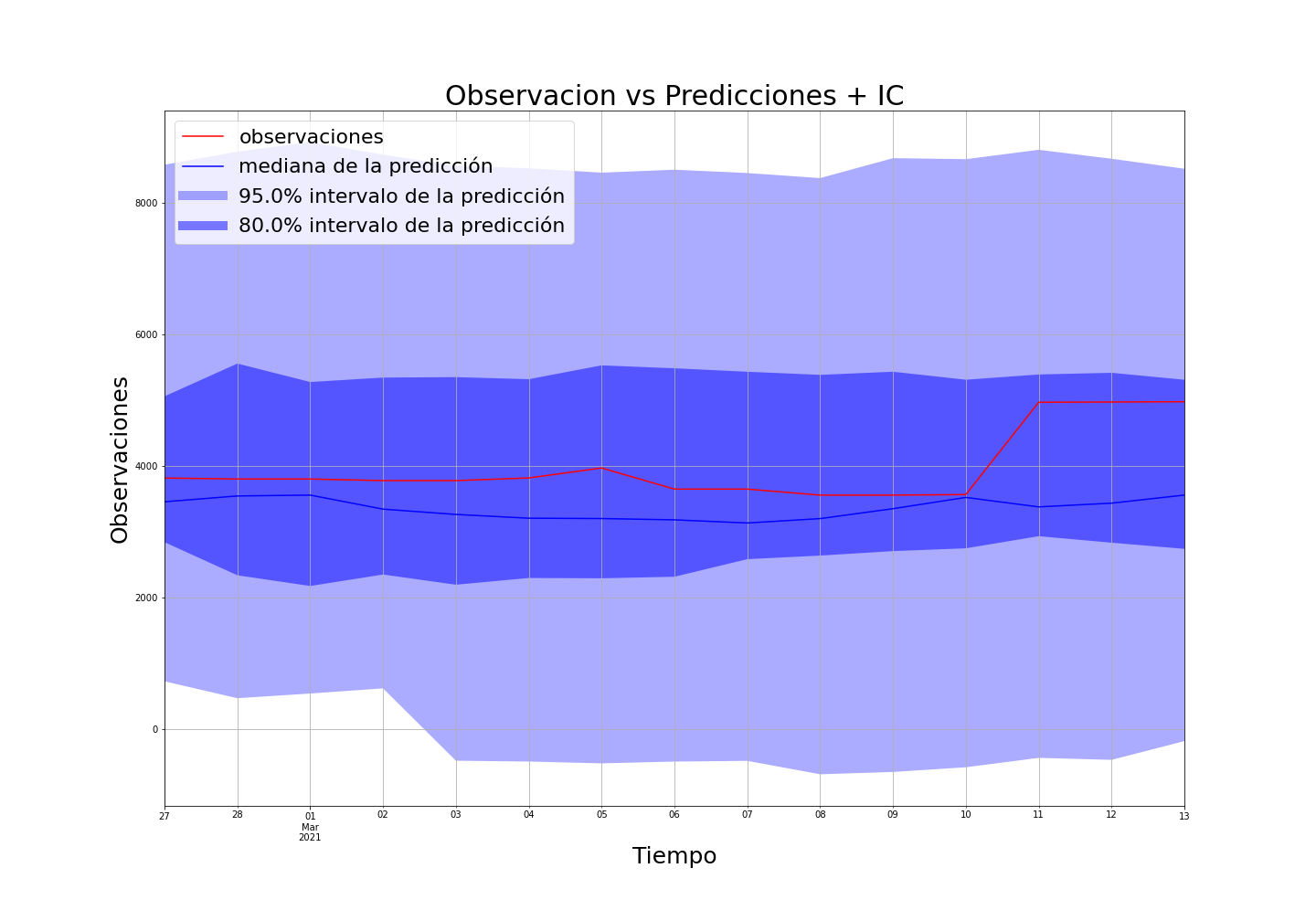
Acá se muestran algunos resultados
Ejemplos de casos no tan buenos
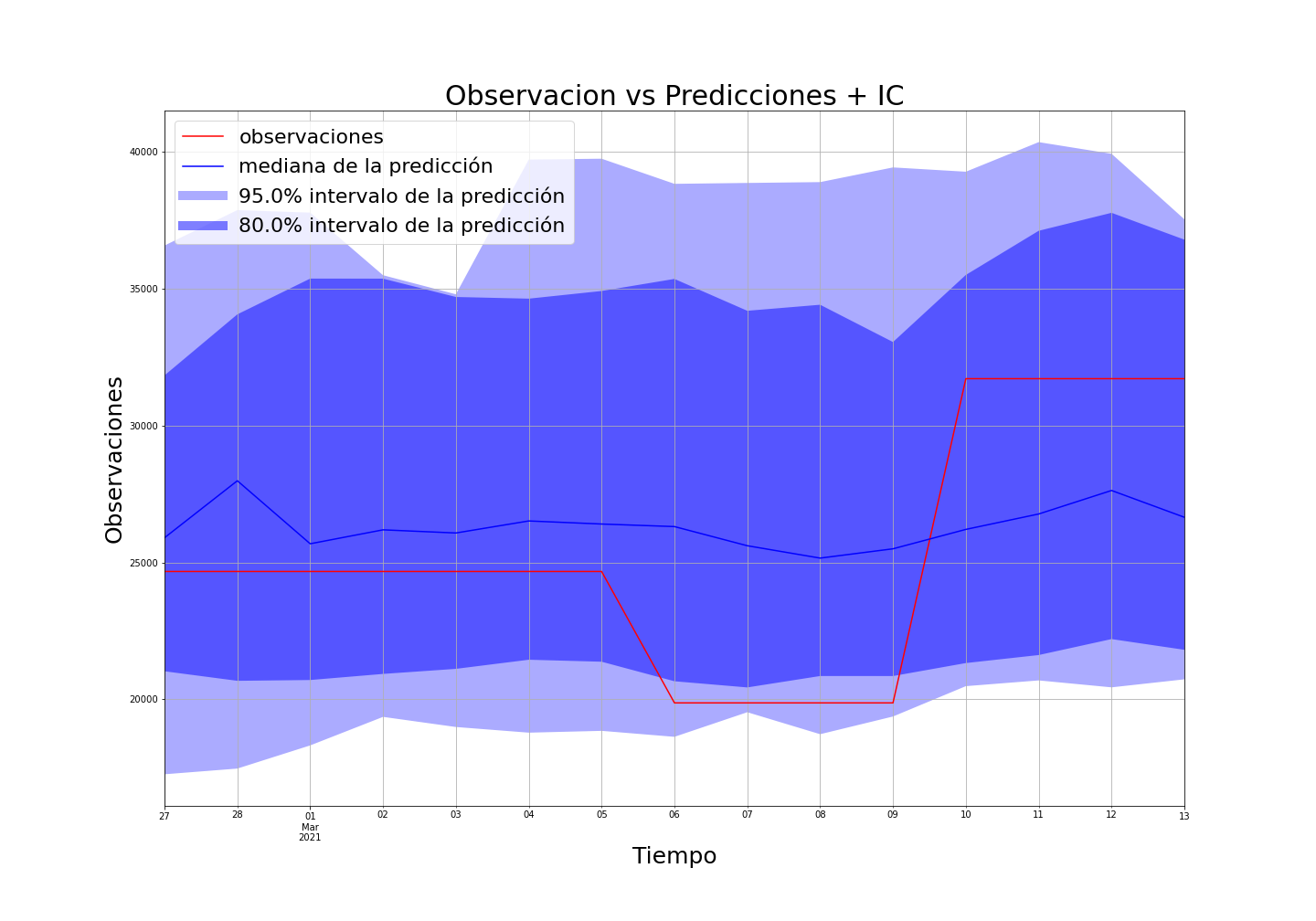
Llegados a este punto, el caso de manufactura puede ser resuelto siempre y cuando se encuentre una forma de suavizar las curvas de demanda, ya que como vimos en los casos de LSTM, estos solo funcionan cuando se suaviza el problema a través de una media movil, la cual no es posible volver atrás y hacer predicciones. Seamos sinceros. Cualquiera que haya trabajado en problemas de predicción de series temporales en el retail, logística, el e-commerce, etc. definitivamente habría maldecido esa serie que se comporta de manera intermitente y arbitraríá. La temida serie temporal intermitente que dificulta el trabajo de un forescaster. Esta molestia hace que la mayoría de las técnicas de pronóstico estándar sean impracticables, plantea preguntas sobre las métricas (ya que mape no puede ser usado), la selección del modelo (pasando desde una amplia gama), el conjunto de modelos, lo que sea. Y para empeorar las cosas, puede haber casos (como en la industria de las piezas de manufactura, repuestos, donde aparecen patrones intermitentes, artículos de movimiento lento pero muy críticos o de alto valor, casos en minería).
Nos basaremos en lo que se entrega en el paper [paper](./documents/paper-intermittent demand forecasting with deep renewal processes.pdf), toda esta revisión bibliográfica viene de los autores Ali Canner, Tim Janushowski, Yuyang Wang y Ali Taylan.
- **Notación: **
- Y - i-ésimo elemento de la serie temporal
- n - El índice de series temporales
- i - El índice de demanda distinta de cero
- Qi: el intervalo entre demanda, es decir, la brecha entre dos demandas distintas de cero.
- Mi- El tamaño de la demanda en un punto de demanda distinto de cero.
Tradicionalmente, existe una clase de algoritmos que toman un camino ligeramente diferente para pronosticar las series de tiempo intermitentes. Este conjunto de algoritmos consideró la demanda intermitente en dos partes (tamaño de la demanda e intervalo entre demanda) y los modeló por separado.
Croston propuso aplicar un único suavizado exponencial por separado a M y Q, como se muestra a continuación:
Después de obtener estas estimaciones, el pronóstico final:
Y este es un pronóstico de un paso adelante y si tenemos que extenderlo a varios pasos de tiempo, nos quedamos con un pronóstico plano con el mismo valor.
Syntetos y Boylan, 2005, mostraron que el pronóstico de Croston estaba sesgado en la demanda intermitente y propuso una corrección con el β de la estimación del intervalo entre demanda.
Shale, Boylan y Johnston (2006) derivaron el sesgo esperado cuando la llegada sigue un proceso de Poisson.
El proceso de renovación es un proceso de llegada en el que los intervalos entre llegadas son variables aleatorias (RV) positivas, independientes e idénticamente distribuidas (IID). Esta formulación generaliza el proceso de Poison durante largos períodos de tiempo arbitrarios. Por lo general, en un proceso de Poisson, los intervalos entre demanda se distribuyen exponencialmente (suposición fuerte). Pero los procesos de renovación tienen un i.i.d. tiempo entre demanda que tiene una media finita. Turkmen et al. 2019 arroja a Croston y sus variantes en un molde de proceso de renovación. Las variables aleatorias, M y Q, ambas definidas en números enteros positivos definen completamente la Yn (ver más arribita la notación)
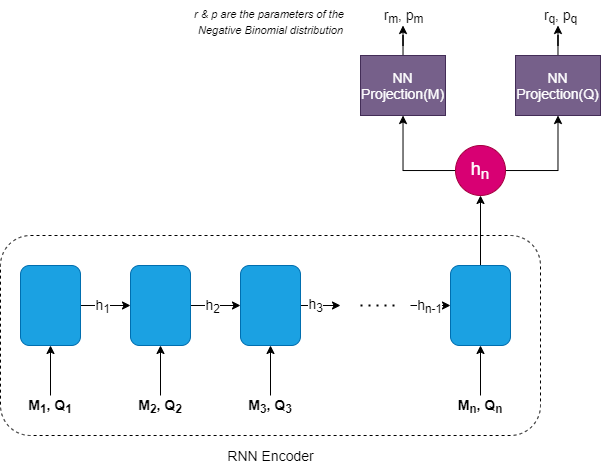
Una vez que el pronóstico de Croston fue presentado como un proceso de renovación, Turkmen et al. propuso estimarlos utilizando una red recurrente (RNN) separada para cada “Tamaño de la demanda” e “Intervalo entre demanda”.
donde:
Esto significa que tenemos una sola RNN, que toma como entrada tanto M como Q y codifica esa información en un encoder (h). Y luego se colocan dos capas NN separadas encima de esta capa oculta para estimar la distribución de probabilidad de M y Q. Tanto para M como para Q, la distribución binomial negativa es la opción sugerida por el artículo, dada esta intermitencia en la demanda.
La distribución binomial negativa es una distribución de probabilidad discreta que se utiliza comúnmente para modelar datos de recuento. Por ejemplo, la cantidad de unidades de un SKU vendidas, la cantidad de personas que visitaron un sitio web o la cantidad de llamadas de servicio que recibe un centro de llamadas, llegadas a una estación de servicio de combustible, etc.
La distribución se deriva de una secuencia de ensayos de Bernoulli, que dice que solo hay dos resultados para cada experimento. Un ejemplo clásico es el lanzamiento de una moneda, que puede ser cara o cruz. Entonces, la probabilidad de éxito es p y el fracaso es 1-p (en un lanzamiento de moneda justo, esto es 0.5 cada uno). Entonces, si seguimos realizando este experimento hasta que veamos r éxitos, el número de fallas que veamos tendrá una distribución binomial negativa.
El significado semántico de éxito y fracaso no tiene por qué ser cierto cuando aplicamos esto, pero lo que importa es que solo hay dos tipos de resultados.
El documento solo habla de pronósticos de un paso adelante, que es también lo que encontrará en mucha literatura sobre Pronósticos de demanda intermitente. Pero en un mundo real, necesitaríamos más tiempo para planificar correctamente. Ya sea que se trate de Croston o de un deep renewal process, la forma en que generamos un pronóstico de n pasos adelante es el mismo: un pronóstico plano de tamaño de la demanda (M) / tiempo entre demanda (Q).
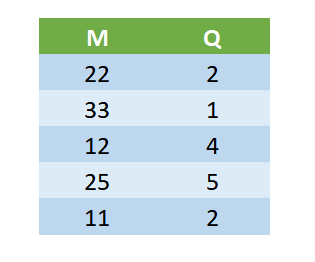
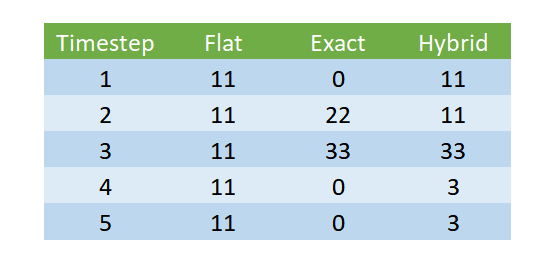
Hemos introducido dos nuevos métodos para decodificar el output, Exact e Hybrid, además del método Flat existente. Suponga que entrenamos el modelo con una longitud de predicción de 5.
La salida sin procesar del modo sería:
-
Flat: En la decodificación plana, solo elegiríamos el primer conjunto de salidas (M = 22 y Q = 2) y generaríamos un pronóstico de un paso adelante y extenderíamos el mismo pronóstico para los 5 pasos de tiempo.
-
Exact La decodificación exacta es una versión más segura de la decodificación. Aquí predecimos una demanda de tamaño de demanda M, cada tiempo entre demanda de Q y hacemos que el resto del pronóstico sea cero.
-
Hibrid En la decodificación híbrida, combinamos estos dos para generar un pronóstico que también tiene en cuenta los cambios a largo plazo en las expectativas del modelo. Usamos el valor M / Q para el pronóstico, pero actualizamos el valor M / Q en función de los siguientes pasos. Por ejemplo, en el ejemplo que tenemos, pronosticaremos 11 (que es 22/3) para los primeros 2 pasos de tiempo, y luego pronosticaremos 33 (que es 33/1) para el siguiente paso de tiempo, etc.
El algoritomo esta usando GluonTS, que es un marco para el pronóstico de series de tiempo neuronales, construido sobre MXNet. AWS Labs está detrás del proyecto de código abierto y algunos de los algoritmos como DeepAR son utilizados internamente por Amazon para producir estos pronósticos. Nosotros nos colgaremos de la librería deeprenewal para hacer estas predicciones, trayendonos el objeto modelo desde ahí.
codes/manufacturing/deep_renewal.py Fallé en el uso de GPU, gluonts no tiene incorporado cudann11, que es lo que ocupa la gpu que ocupo, se demorá mucho si no tienes GPU, voy intentar probarlo por SageMaker, pero puede tener costo, se demorá infinito solo en CPU.
El issue sigue abierto: