ZOOpt

ZOOpt is a python package for Zeroth-Order Optimization.

Zeroth-order optimization (a.k.a. derivative-free optimization/black-box optimization) does not rely on the gradient of the objective function, but instead, learns from samples of the search space. It is suitable for optimizing functions that are nondifferentiable, with many local minima, or even unknown but only testable.

ZOOpt implements some state-of-the-art zeroth-order optimization methods and their parallel versions. Users only need to add several keywords to use parallel optimization on a single machine. For large-scale distributed optimization across multiple machines, please refer to Distributed ZOOpt.

Documents: Tutorial of ZOOpt

Citation:

Yu-Ren Liu, Yi-Qi Hu, Hong Qian, Yang Yu, Chao Qian. ZOOpt: Toolbox for Derivative-Free Optimization. CORR abs/1801.00329

(Features in this article are from version 0.2)

Installation

The easiest way to install ZOOpt is to type pip install zoopt in the terminal/command line.

Alternatively, to install ZOOpt by source code, download this repository and sequentially run following commands in your terminal/command line.

$ python setup.py build
$ python setup.py install

Quick tutorial for `Dimension2` class

Since release 0.4.1, Dimension2 class in ZOOpt supports constructing THREE types of dimensions, i.e.: ValueType.CONTINUOUS, ValueType.DISCRETE, and ValueType.GRID.

For continuous dimensions, the arguments should be like (ValueType.CONTINUOUS, range, float_precision).
Where ValueType.CONTINUOUS indicates this dimension is continuous. range is a list that indicates the search space, such as [min, max] (endpoints are inclusive). float_precision means the precision of this dimension, e.g., if it is set to 1e-6, 0.001, or 10, the answer will be accurate to six decimal places, three decimal places, or tens places.

For discrete dimensions, the arguments should be like (ValueType.DISCRETE, range, has_partial_order).
Where ValueType.DISCRETE indicates this dimension is discrete. range is also a list that indicates the search space, such as [min, max] (endpoints are inclusive), but ONLY integers can be sampled. has_partial_order means whether this dimension is ordered. True is for an ordered relation and False means not.

For grid dimensions, the arguments should be like (ValueType.GRID, grid_list).
Where ValueType.GRID indicates this dimension is a grid, which is convenient to instance-wise search. grid_list is a list whose values can be str, int, float, etc. All values in this list will be sampled like grid search.

For instance, you can define your own dimensions like:

dim_list = [
    (ValueType.CONTINUOUS, [-1, 1], 1e-6),
    (ValueType.DISCRETE, [-10, 10], False),
    (ValueType.DISCRETE, [10, 100], True),
    (ValueType.GRID, [64, 128, 256, 512, 1024]),
    (ValueType.GRID, ["relu", "leaky_relu", "tanh", "sigmoid"])
]

dim = Dimension2(dim_list)

A simple example

We define the Ackley function for minimization (note that this function is for arbitrary dimensions, determined by the solution)

import numpy as np
def ackley(solution):
    x = solution.get_x()
    bias = 0.2
    value = -20 * np.exp(-0.2 * np.sqrt(sum([(i - bias) * (i - bias) for i in x]) / len(x))) - \
            np.exp(sum([np.cos(2.0*np.pi*(i-bias)) for i in x]) / len(x)) + 20.0 + np.e
    return value

Ackley function is a classical function with many local minima. In 2-dimension, it looks like (from wikipedia)

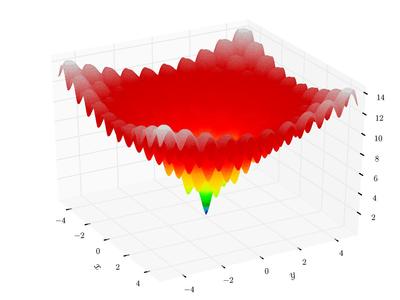Then, use ZOOpt to optimize a 100-dimension Ackley function:

from zoopt import Dimension, ValueType, Dimension2, Objective, Parameter, Opt, ExpOpt

dim_size = 100  # dimension size
dim = Dimension(dim_size, [[-1, 1]]*dim_size, [True]*dim_size)  
# dim = Dimension2([(ValueType.CONTINUOUS, [-1, 1], 1e-6)]*dim_size)
obj = Objective(ackley, dim)
# perform optimization
solution = Opt.min(obj, Parameter(budget=100*dim_size))
# print the solution
print(solution.get_x(), solution.get_value())
# parallel optimization for time-consuming tasks
solution = Opt.min(obj, Parameter(budget=100*dim_size, parallel=True, server_num=3))

For a few seconds, the optimization is done. Then, we can visualize the optimization progress

import matplotlib.pyplot as plt
plt.plot(obj.get_history_bestsofar())
plt.savefig('figure.png')

which looks like

We can also use `ExpOpt` to repeat the optimization for performance analysis, which will calculate the mean and standard deviation of multiple optimization results while automatically visualizing the optimization progress.

solution_list = ExpOpt.min(obj, Parameter(budget=100*dim_size), repeat=3,
                           plot=True, plot_file="progress.png")
for solution in solution_list:
		print(solution.get_x(), solution.get_value())

More examples are available in the example fold.

Releases

release 0.4.1

Fix known bugs when sampling for Tune and compatible with the latest Ray 0.8.7. It is strongly recommended to update to this version if you are leveraging Ray.
Add ValueType.GRID for instance-wise search in Dimension2 class.

release 0.4

Add Dimension2 class, which provides another format to construct dimensions. Unlike Dimension class, Dimension2 allows users to specify optimization precision.
Add SRacosTune class, which is used to suggest/provide trials and process results for Tune (a platform based on RAY for distributed model selection and training).
Deprecate Python 2 support

release 0.3

Add a parallel implementation of SRACOS, which accelarates the optimization by asynchronous parallelization.
Add a function that enables users to set a customized stop criteria for the optimization.
Rewrite the documentation to make it easier to follow.

release 0.2

Add the noise handling strategies Re-sampling and Value Suppression (AAAI'18), and the subset selection method with noise handling PONSS (NIPS'17)
Add high-dimensionality handling method Sequential Random Embedding (IJCAI'16)
Rewrite Pareto optimization method. Bugs fixed.

release 0.1

Include the general optimization method RACOS (AAAI'16) and Sequential RACOS (AAAI'17), and the subset selection method POSS (NIPS'15).
The algorithm selection is automatic. See examples in the example fold.- Default parameters work well on many problems, while parameters are fully controllable
Running speed optmized for Python

Distributed ZOOpt

Distributed ZOOpt is consisted of a server project and a client project. Details can be found in the Tutorial of Distributed ZOOpt

mittalgovind/ZOOpt