nGMCA - non-negative Generalized Morphological Component Analysis

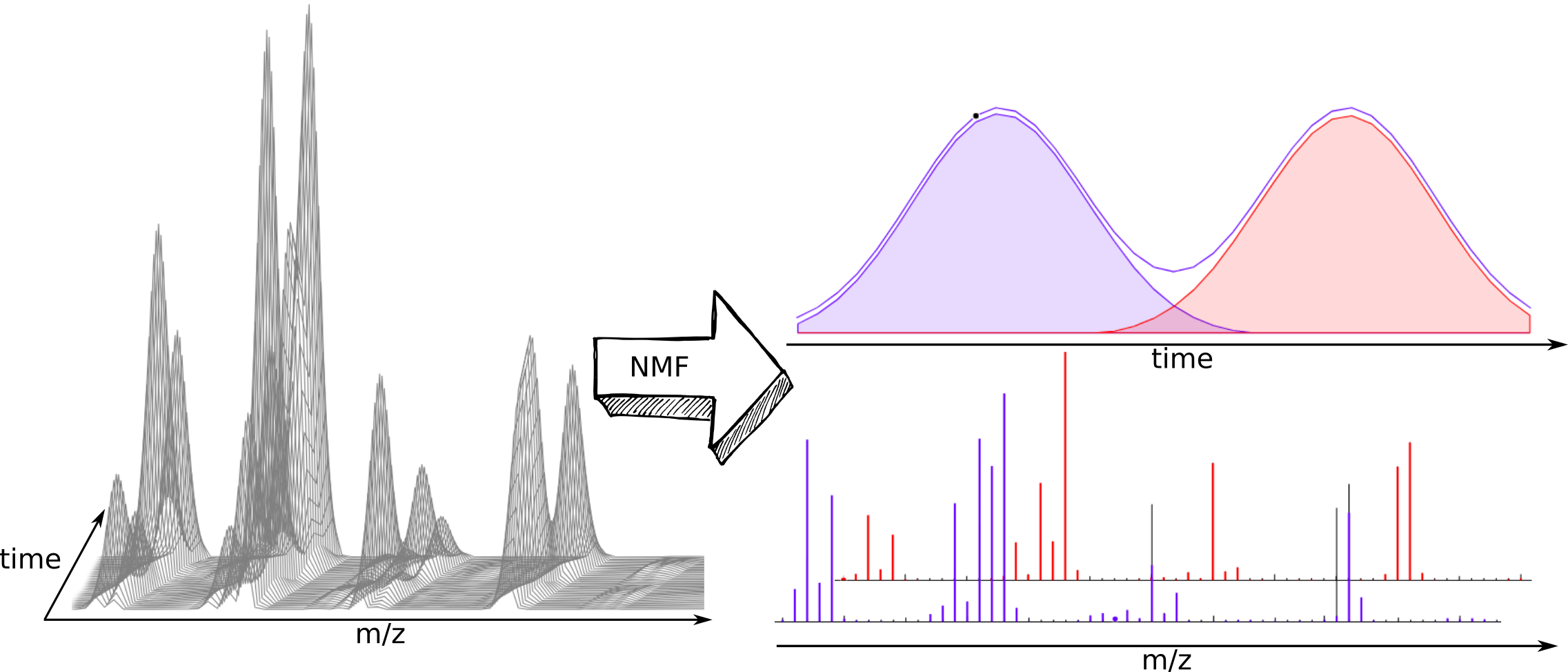
A tool for non-negative matrix factorization.

Instalation

$ npm install ml-ngmca

Usage

import { nGMCA } from 'ml-ngmca';

const result = nGMCA(dataMatrix, options);

As a CommonJS module

const { nGMCA } = require('ml-ngmca');

const result = nGMCA(dataMatrix, options);

API Documentation

This algorithm is based on the article Jérémy Rapin, Jérôme Bobin, Anthony Larue, Jean-Luc Starck. Sparse and Non-negative BSS for Noisy Data, IEEE Transactions on Signal Processing, 2013.IEEE Transactions on Signal Processing, vol. 61, issue 22, p. 5620-5632, 2013.

In order to get a general idea of the problem you could also check the Wikipedia article.

Examples

You will be able to separate the components of a mixture if you have a series of measurements correlated by a composition profile e.g NMR or mass spectra coming from a chromatographic coupled technique of two or more close retention times. So you will have a matrix with a number of rows equal or greater than the number of pure components of the mixture.

import { Matrix } from 'ml-matrix';
import { nGMCA } from 'ml-ngmca';

let pureSpectra = new Matrix([[1, 0, 1, 0]]);
let composition = new Matrix([[1, 2, 3, 2, 1]]);

// matrix = composition.transpose().mmul(pureSpectra)
let matrix = new Matrix([
  [1, 0, 1, 0],
  [2, 0, 2, 0],
  [3, 0, 3, 0],
  [2, 0, 2, 0],
  [1, 0, 1, 0],
]);

const options = {
  maximumIteration: 200,
  phaseRatio: 0.4,
};
const result = nGMCA(matrix, 1, options);
const { A, S } = result;
console.log(`A = ${A.to2DArray()} S =${S.to2DArray()}`);
/**
A = [
    [ 0.22941573387056177 ],
    [ 0.45883146774112354 ],
    [ 0.6882472016116853 ],
    [ 0.45883146774112354 ],
    [ 0.22941573387056177 ]
  ]
S = [ [ 4.358898943540674, 0, 4.358898943540674, 0 ] ]

if you reescale both S maxS and A with 1/maxS.
*/

let maxByRow = [];
for (let i = 0; i < S.rows; i++) {
  maxByRow.push(S.maxRow(i));
}

S.scale('row', { scale: maxByRow });
A.scale('column', {
  scale: maxByRow.map((e) => 1 / e),
});

/**
S = [ [ 1, 0, 1, 0 ] ]
A = [
  [1.0000000000000002],
  [2.0000000000000004],
  [3.0000000000000004],
  [2.0000000000000004],
  [1.0000000000000002]
  ]
*/

const estimatedMatrix = A.mmul(S);
const diff = Matrix.sub(matrix, estimatedMatrix);

Here is a second example:

let matrix = new Matrix([
  [0, 0, 1, 1, 1],
  [0, 0, 1, 1, 1],
  [2, 2, 2, 0, 0],
  [2, 2, 2, 0, 0],
]);

const options = {
  maximumIteration: 200,
  phaseRatio: 0.4,
};
const result = nGMCA(matrix, 1, options);
const { A, S } = result;
console.log(`A = ${A} S =${S}`);
/**
 A = [
  [
    0.707107 0       
    0.707107 0       
    2.26e-17 0.707107
    2.26e-17 0.707107
  ]
]
S = [
  [
    9.86e-32 9.86e-32 1.41421 1.41421 1.41421
    2.82843  2.82843  2.82843 0       0       
  ]
]
note: 9.86e-32 and 2.26e-17 is practically zero
so if you reescale both S maxS and A with 1/maxS.
*/

let maxByRow = [];
for (let i = 0; i < S.rows; i++) {
  maxByRow.push(S.maxRow(i));
}

S.scale('row', { scale: maxByRow });
A.scale('column', {
  scale: maxByRow.map((e) => 1 / e),
});

console.log(`A = ${A} S =${S}`);
/**
 A = [
  [
    1 0       
    1 0       
    0 1
    0 1
  ]
]
S = [
  [
    0 0 1 1 1
    2 2 2 0 0       
  ]
]
*/

The result has the matrices A and S, the estimated matrices of compositions and pureSpectra respectively. It's possible that the matrices A and S have not the same scale than pureSpectra and composition matrices because of AS has an infinity of combination to get the target matrix.

License

MIT

mljs/nGMCA