shapiq: Shapley Interactions for Machine Learning

An interaction may speak more than a thousand main effects.

Shapley Interaction Quantification (shapiq) is a Python package for (1) approximating any-order Shapley interactions, (2) benchmarking game-theoretical algorithms for machine learning, (3) explaining feature interactions of model predictions. shapiq extends the well-known shap package for both researchers working on game theory in machine learning, as well as the end-users explaining models. SHAP-IQ extends individual Shapley values by quantifying the synergy effect between entities (aka players in the jargon of game theory) like explanatory features, data points, or weak learners in ensemble models. Synergies between players give a more comprehensive view of machine learning models.

🛠️ Install

shapiq is intended to work with Python 3.9 and above. Installation can be done via pip:

pip install shapiq

⭐ Quickstart

You can explain your model with shapiq.explainer and visualize Shapley interactions with shapiq.plot. If you are interested in the underlying game theoretic algorithms, then check out the shapiq.approximator and shapiq.games modules.

📈 Compute any-order feature interactions

Explain your models with Shapley interaction values like the k-SII values:

import shapiq
# load data
X, y = shapiq.load_california_housing(to_numpy=True)
# train a model
from sklearn.ensemble import RandomForestRegressor
model = RandomForestRegressor()
model.fit(X, y)
# set up an explainer with k-SII interaction values up to order 4
explainer = shapiq.TabularExplainer(
    model=model,
    data=X,
    index="k-SII",
    max_order=4
)
# explain the model's prediction for the first sample
interaction_values = explainer.explain(X[0], budget=256)
# analyse interaction values
print(interaction_values)

>> InteractionValues(
>>     index=k-SII, max_order=4, min_order=0, estimated=False,
>>     estimation_budget=256, n_players=8, baseline_value=2.07282292,
>>     Top 10 interactions:
>>         (0,): 1.696969079  # attribution of feature 0
>>         (0, 5): 0.4847876
>>         (0, 1): 0.4494288  # interaction between features 0 & 1
>>         (0, 6): 0.4477677
>>         (1, 5): 0.3750034
>>         (4, 5): 0.3468325
>>         (0, 3, 6): -0.320  # interaction between features 0 & 3 & 6
>>         (2, 3, 6): -0.329
>>         (0, 1, 5): -0.363
>>         (6,): -0.56358890
>> )

📊 Visualize feature interactions

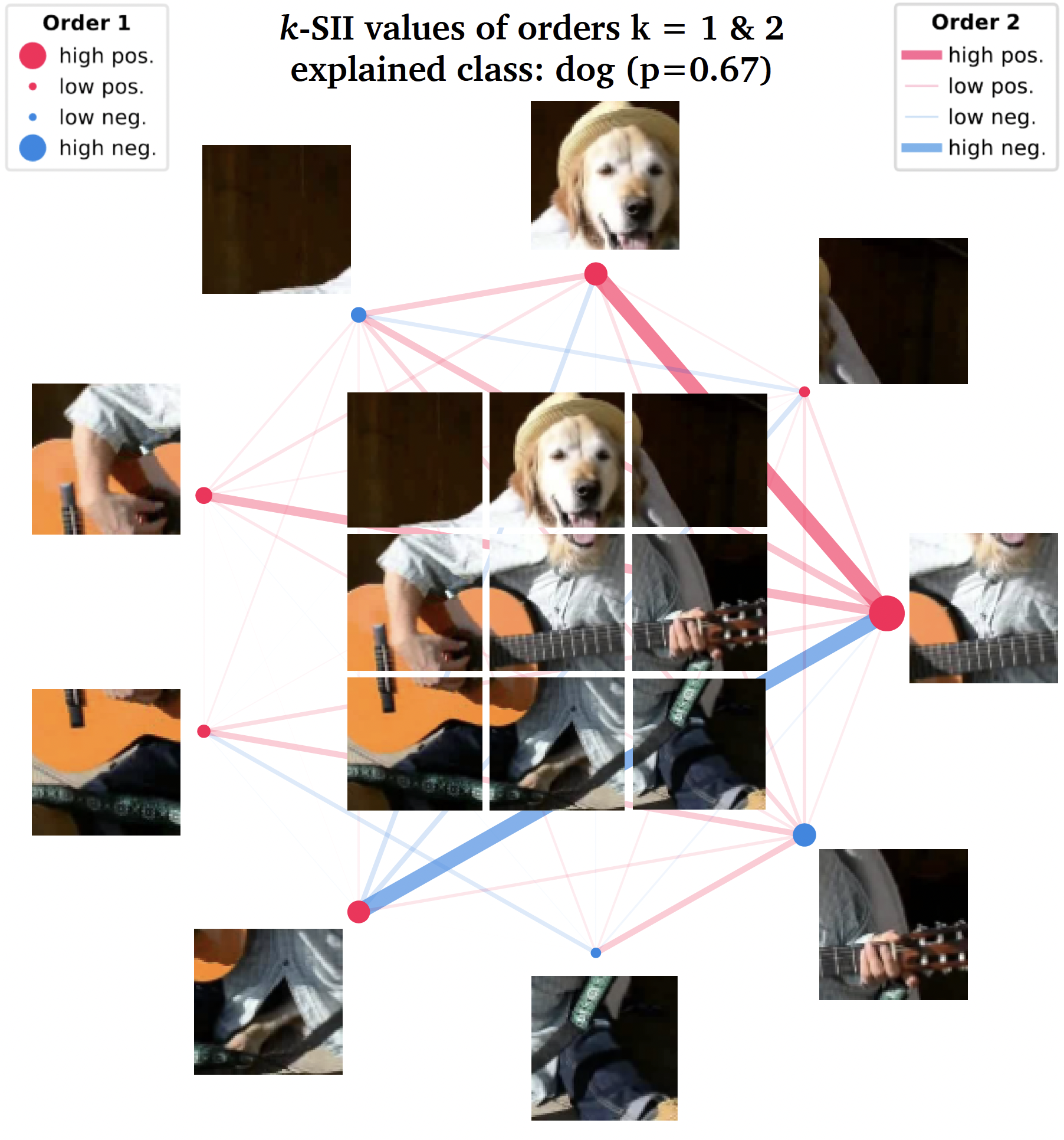
A handy way of visualizing interaction scores up to order 2 are network plots. You can see an example of such a plot below. The nodes represent feature attributions and the edges represent the interactions between features. The strength and size of the nodes and edges are proportional to the absolute value of attributions and interactions, respectively.

shapiq.network_plot(
    first_order_values=interaction_values.get_n_order_values(1),
    second_order_values=interaction_values.get_n_order_values(2)
)
# or use
interaction_values.plot_network()

The pseudo-code above can produce the following plot (here also an image is added):

📖 Documentation with tutorials

The documentation of shapiq can be found at https://shapiq.readthedocs.io

💬 Citation

If you use the shapiq package, please cite our NeurIPS paper:

@inproceedings{muschalik2024shapiq,
  title     = {shapiq: Shapley Interactions for Machine Learning},
  author    = {Maximilian Muschalik and Hubert Baniecki and Fabian Fumagalli and
               Patrick Kolpaczki and Barbara Hammer and Eyke H\"{u}llermeier},
  booktitle = {NeurIPS},
  year      = {2024}
}