tfcausalimpact

Google's Causal Impact Algorithm Implemented on Top of TensorFlow Probability.

How It Works

The algorithm basically fits a Bayesian structural model on past observed data to make predictions on what future data would look like. Past data comprises everything that happened before an intervention (which usually is the changing of a variable as being present or not, such as a marketing campaign that starts to run at a given point). It then compares the counter-factual (predicted) series against what was really observed in order to extract statistical conclusions.

Running the model is quite straightforward, it requires the observed data y, covariates X that helps the model through a linear regression, a pre-period interval that selects everything that happened before the intervention and a post-period with data after the "impact" happened.

Please refer to this medium post for more on this subject.

Installation

pip install tfcausalimpact

Requirements

python{3.6, 3.7, 3.8}
numpy
matplotlib
jinja2
tensorflow>=2.3.0
tensorflow_probability>=0.11.0

Getting Started

We recommend this presentation by Kay Brodersen (one of the creators of the Causal Impact in R).

We also created this introductory ipython notebook with examples of how to use this package.

This medium article also offers some ideas and concepts behind the library.

Example

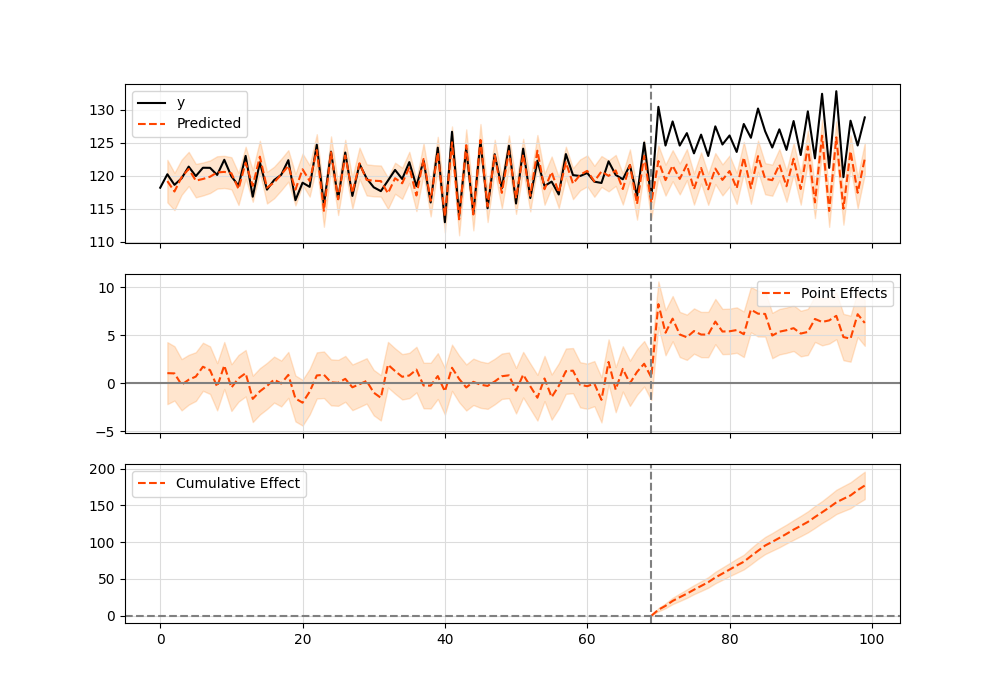
Here's a simple example (which can also be found in the original Google's R implementation) running in Python:

import pandas as pd
from causalimpact import CausalImpact


data = pd.read_csv('https://raw.githubusercontent.com/WillianFuks/tfcausalimpact/master/tests/fixtures/arma_data.csv')
data.iloc[70:, 0] += 5

pre_period = [0, 69]
post_period = [70, 99]

ci = CausalImpact(data, pre_period, post_period)
print(ci.summary())
print(ci.summary(output='report'))
ci.plot()

Summary should look like this:

Posterior Inference {Causal Impact}
                          Average            Cumulative
Actual                    125.23             3756.86
Prediction (s.d.)         120.34 (0.31)      3610.28 (9.28)
95% CI                    [119.76, 120.97]   [3592.67, 3629.06]

Absolute effect (s.d.)    4.89 (0.31)        146.58 (9.28)
95% CI                    [4.26, 5.47]       [127.8, 164.19]

Relative effect (s.d.)    4.06% (0.26%)      4.06% (0.26%)
95% CI                    [3.54%, 4.55%]     [3.54%, 4.55%]

Posterior tail-area probability p: 0.0
Posterior prob. of a causal effect: 100.0%

For more details run the command: print(impact.summary('report'))

And here's the plot graphic:

Google R Package vs TensorFlow Python

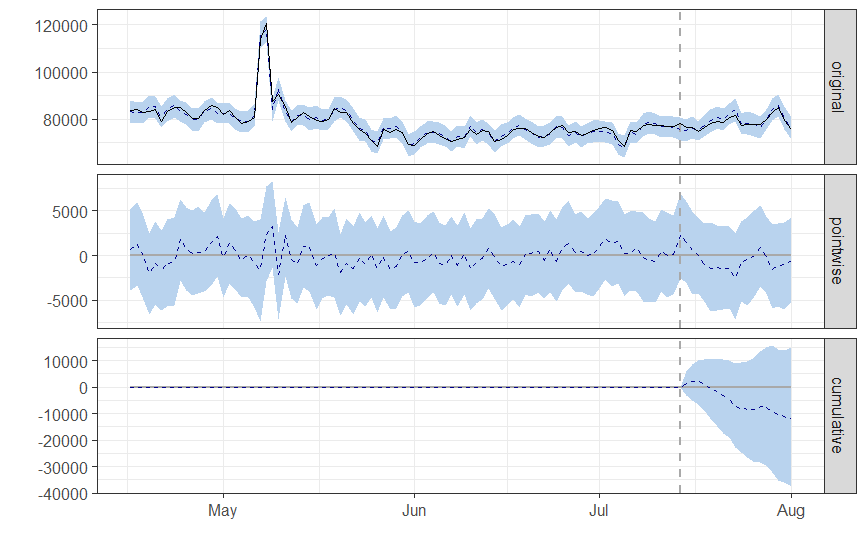
Both packages should give equivalent results. Here's an example using the comparison_data.csv dataset available in the fixtures folder. When running CausalImpact in the original R package, this is the result:

R

data = read.csv.zoo('comparison_data.csv', header=TRUE)
pre.period <- c(as.Date("2019-04-16"), as.Date("2019-07-14"))
post.period <- c(as.Date("2019-07-15"), as.Date("2019-08-01"))
ci = CausalImpact(data, pre.period, post.period)

Summary results:

Posterior inference {CausalImpact}

                         Average          Cumulative        
Actual                   78574            1414340           
Prediction (s.d.)        79232 (736)      1426171 (13253)   
95% CI                   [77743, 80651]   [1399368, 1451711]
                                                            
Absolute effect (s.d.)   -657 (736)       -11831 (13253)    
95% CI                   [-2076, 832]     [-37371, 14971]   
                                                            
Relative effect (s.d.)   -0.83% (0.93%)   -0.83% (0.93%)    
95% CI                   [-2.6%, 1%]      [-2.6%, 1%]       

Posterior tail-area probability p:   0.20061
Posterior prob. of a causal effect:  80%

For more details, type: summary(impact, "report")

And correspondent plot:

Python

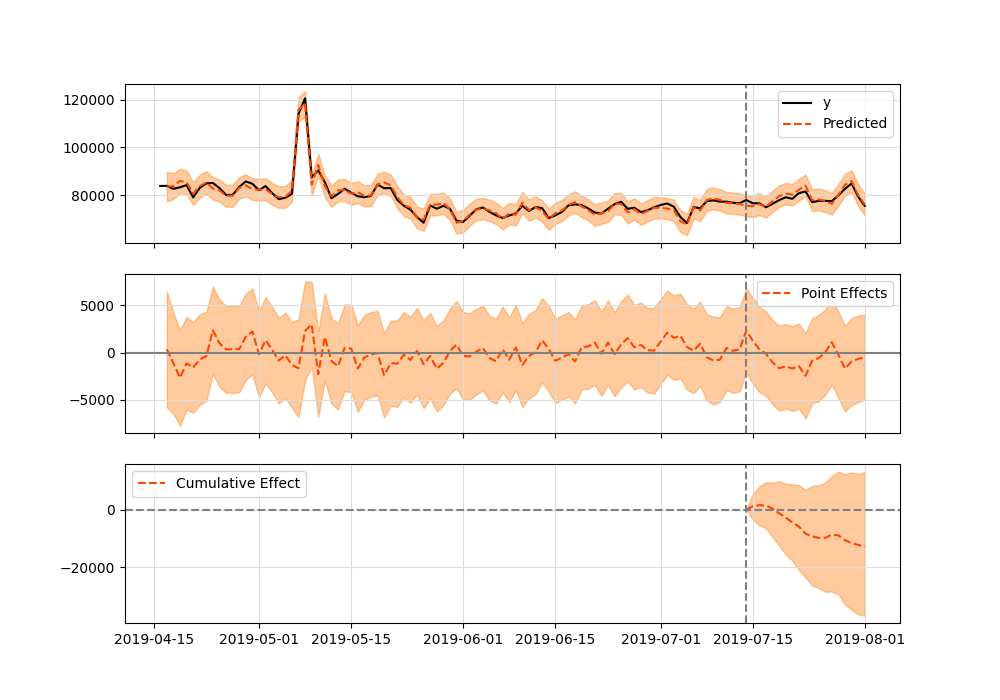
import pandas as pd
from causalimpact import CausalImpact


data = pd.read_csv('tests/fixtures/comparison_data.csv', index_col=['DATE'])
pre_period = ['2019-04-16', '2019-07-14']
post_period = ['2019-7-15', '2019-08-01']
ci = CausalImpact(data, pre_period, post_period, model_args={'fit_method': 'hmc'})

Summary is:

Posterior Inference {Causal Impact}
                          Average            Cumulative
Actual                    78574.42           1414339.5
Prediction (s.d.)         79282.92 (727.48)  1427092.62 (13094.72)
95% CI                    [77849.5, 80701.18][1401290.94, 1452621.31]

Absolute effect (s.d.)    -708.51 (727.48)   -12753.12 (13094.72)
95% CI                    [-2126.77, 724.92] [-38281.81, 13048.56]

Relative effect (s.d.)    -0.89% (0.92%)     -0.89% (0.92%)
95% CI                    [-2.68%, 0.91%]    [-2.68%, 0.91%]

Posterior tail-area probability p: 0.16
Posterior prob. of a causal effect: 84.12%

For more details run the command: print(impact.summary('report'))

And plot:

Both results are equivalent.

Performance

This package uses as default the Variational Inference method from TensorFlow Probability which is faster and should work for the most part. Convergence can take somewhere between 2~3 minutes on more complex time series. Also, consider using a GPU to run even faster.

If, on the other hand, precision is the top requirement when running causal impact analyzes, it's possible to switch algorithms by manipulating the input arguments like so:

ci = CausalImpact(data, pre_period, post_period, model_args={'fit_method': 'hmc'})

This will make usage of the algorithm Hamiltonian Monte Carlo which is State-of-the-Art for finding the Bayesian posterior of distributions. Still, keep in mind that on complex time series with thousands of data points and complex modeling involving various seasonal components this optimization can take 1 hour or even more to complete (on a GPU). Performance is sacrificed in exchange for better precision.

Bugs & Issues

If you find bugs or have any issues while running this library please consider opening an Issue with a complete description and reproductible environment so we can better help you solving the problem.

mossydidar/tfcausalimpact