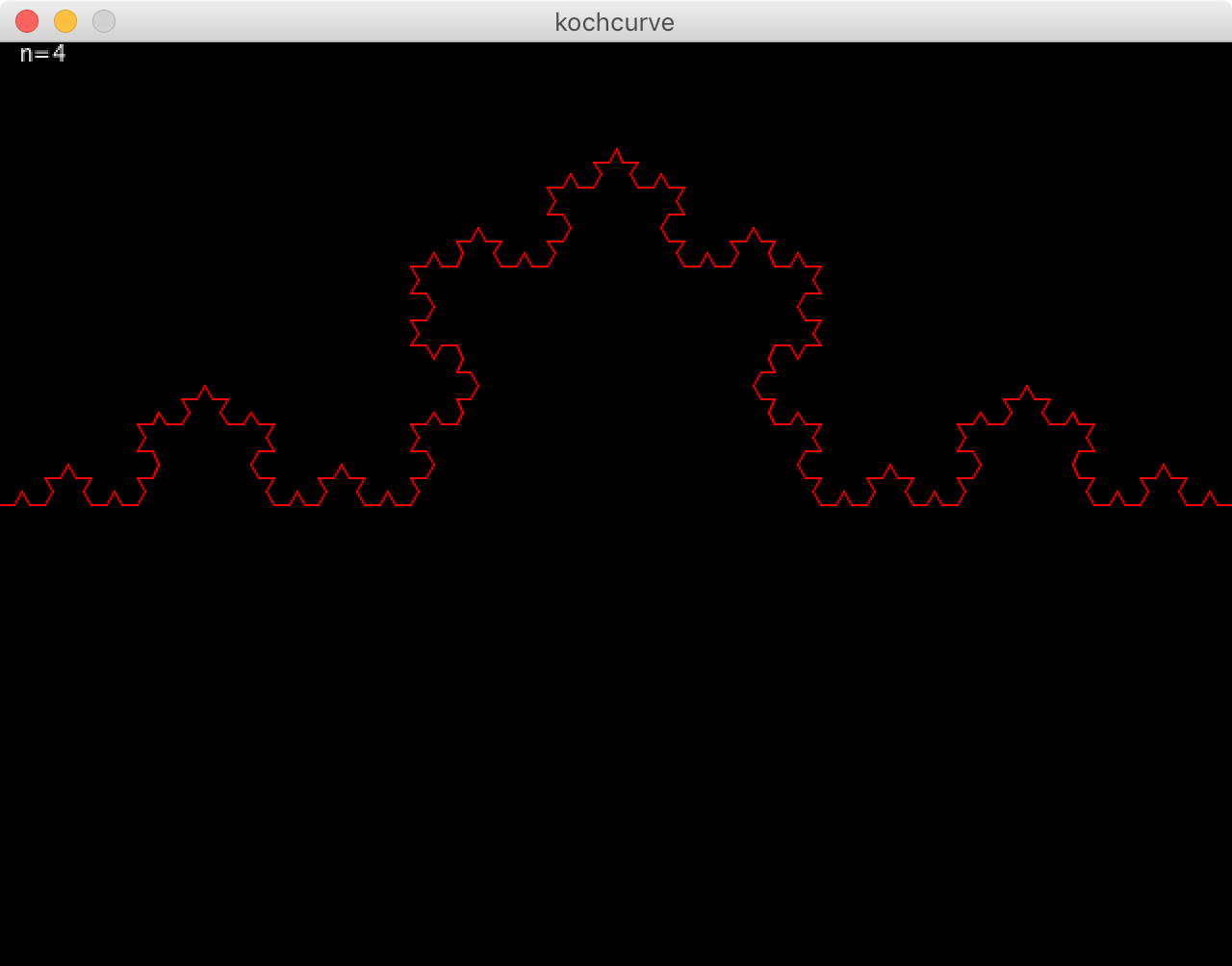
Koch curve, which appeared in a 1904 by Helge von Koch is one of the fractals.
It is shown in this figure.
The source code is written in Processing.
Therefore, you open by Processing3 and run.
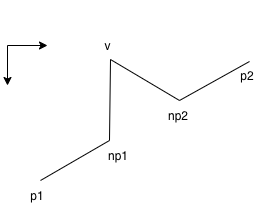
Atomically divide Koch curve. The atomic triangle is shown in this figure.
Divide the line(p1, p2) into three equal lines. This defines two new points(np1, np2). These are points that structure a new triangle.
Point np1 = new Point(0, 0);
Point np2 = new Point(0, 0);
Point v = new Point(0, 0);
np1.x = (2*p1.x + p2.x) / 3.0;
np1.y = (2*p1.y + p2.y) / 3.0;
np2.x = (p1.x + 2*p2.x) / 3.0;
np2.y = (p1.y + 2*p2.y) / 3.0;
Already, np1 and np2 are known as points of a new triangle. Find the last point(v).
First, Seek a midpoint of a line np1-np2.
Second, Add the resolved height(high*cos(angle), high*sin(angle)) x and y. "height" is reserved word.
But, y-coordinates on computer is the inverse of mathematical y-coordinates. Therefore, y direction must be
subtracted from the midpoint.
These values is point v.
float angle, high;
angle = PI/2 - atan2(p2.y - p1.y, p2.x - p1.x);
high = np1.dst(np2) * (sqrt(3) / 2); //sin(PI / 3.0);
v.x = (np1.x + np2.x) / 2.0 + high * cos(angle);
v.y = (np1.y + np2.y) / 2.0 - high * sin(angle);
Already, p1, np1, v, np2, p1 are seeked. draw lines p1-np1, np1-v, v-np2 and np2-pi. Repeat this recursively.
koch(n-1, p1, np1);
koch(n-1, np1, v);
koch(n-1, v, np2);
koch(n-1, np2, p2);