See lqr_infinite_horizon.ipnyb
TODO: add entropy in the value function to add exploration. (We need to know the whole distribution!)
See lqr.py.
We solve the control problem, by minimising J
 where g is convex. The policy alpha is parametrised with a neural network, and we use Method of successive approximations on Pontryagin Maximum principle.
Algorithm:
where g is convex. The policy alpha is parametrised with a neural network, and we use Method of successive approximations on Pontryagin Maximum principle.
Algorithm:
- Start with initial policy
- Solve BSDE using Deep Learning for processes (Yt, Zt).
- Update policy by maximising Hamiltonian (analog to Q-learning on model-free RL)
- Go back to 2.
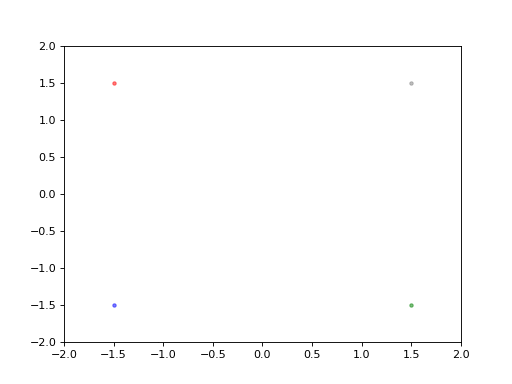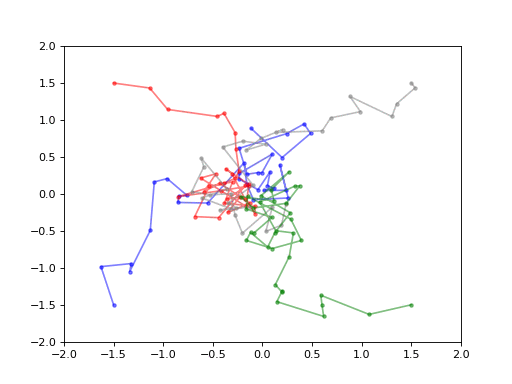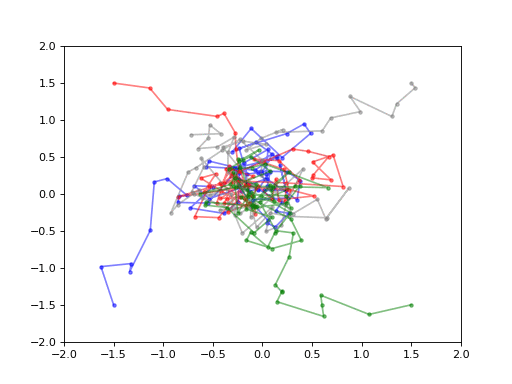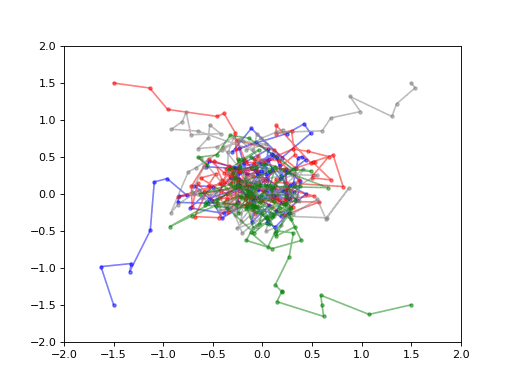
Drunk agents trying to reach the origin (aka LQR: dX_t = a_t dt + dW_t, with running cost f(x,a) = a^2, and final cost g(x) = x^2)
Code is loopy. The bsde solver and the Hamiltonian should be vectorized across time.